介绍线性代数中的基本数学对象、算术和运算，并用数学符号和相应的python代码实现来表示它们

标量/向量/矩阵/dot product/矩阵的乘法相信大家都在线代中学过了，这里只是再回顾一下，并看一看用Python如何实现

1. 张量算法的基本性质

标量、向量、矩阵和任意数量轴的张量（这里的“张量”指代数对象）有一些实用的属性。 例如，任何按元素的一元运算都不会改变其操作数的形状。 同样，给定具有相同形状的任意两个张量，任何按元素二元运算的结果都将是相同形状的张量。 例如，将两个相同形状的矩阵相加，会在这两个矩阵上执行元素加法。

import torch
import numpy as np

A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone()  # 通过分配新内存，将A的一个副本分配给B
#copy与clone的区别（是关于内存的吗）？
#copy有可能是不copy内存的（深度copy与浅copy），clone一定会复制内存
A, A + B，A.T#矩阵的逆

(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.],
         [12., 13., 14., 15.],
         [16., 17., 18., 19.]]),
 tensor([[ 0.,  2.,  4.,  6.],
         [ 8., 10., 12., 14.],
         [16., 18., 20., 22.],
         [24., 26., 28., 30.],
         [32., 34., 36., 38.]])
 tensor([[ 0.,  4.,  8., 12., 16.],
     [ 1.,  5.,  9., 13., 17.],
     [ 2.,  6., 10., 14., 18.],
     [ 3.,  7., 11., 15., 19.]]))

两个矩阵的按元素乘法称为Hadamard积（Hadamard product）（数学符号为$\odot$)。矩阵A和B的Hadamard积为：
$$\begin{array}{rl}A\odot B& =\left[\begin{array}{cccc}{a}_{11}{b}_{11}& a_{12}{b}_{12}& ...& a_{1n}{b}_{1n}\\ a_{21}{b}_{21}& a_{22}{b}_{22}& ...& a_{2n}{b}_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}{b}_{m1}& a_{m2}{b}_{m2}& ...& a_{mn}{b}_{mn}\end{array}\right]\end{array}$$

#两个矩阵按元素相乘称为Hadamard积
A * B

tensor([[  0.,   1.,   4.,   9.],
        [ 16.,  25.,  36.,  49.],
        [ 64.,  81., 100., 121.],
        [144., 169., 196., 225.],
        [256., 289., 324., 361.]])

将张量乘/加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘

#将张量乘/加上一个标量不会改变张量的形状，其中张量的每个元素都将与标量相加或相乘。
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape

(tensor([[[ 2,  3,  4,  5],
          [ 6,  7,  8,  9],
          [10, 11, 12, 13]],
 
         [[14, 15, 16, 17],
          [18, 19, 20, 21],
          [22, 23, 24, 25]]]),
 torch.Size([2, 3, 4]))

2. 降维

降维求和

默认情况下，调用求和函数会沿所有的轴降低张量的维度，使它变为一个标量。 我们还可以指定张量沿哪一个轴来通过求和降低维度。 以矩阵为例，为了通过求和所有行的元素来降维（轴0），我们可以在调用函数时指定axis=0。 由于输入矩阵沿0轴降维以生成输出向量，因此输入轴0的维数在输出形状中消失。

#降维
#我们可以对任意张量进行的一个有用的操作是计算其元素的和
A.shape, A.sum()

(torch.Size([5, 4]), tensor(190.))

A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape

(tensor([40., 45., 50., 55.]), torch.Size([4]))

#指定axis=1将通过汇总所有列的元素降维（轴1）。因此，输入轴1的维数在输出形状中消失。
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape

(tensor([ 6., 22., 38., 54., 70.]), torch.Size([5]))

这里可以这样理解，指定axis = 0，即是矩阵的第一维(在本例子中为A的行)，在求sum时axis = 表明按照行去做的，而行的方向是向下的，所以按照axis = 0求和的结果第一个元素为0+4+8+12+16=40

axis = 0按照行，可以理解为把“行”给抹去只剩1行，也就是上下压扁。
axis = 1按照列，可以理解为把“列”给抹去只剩1列，也就是左右压扁。（当拓展到多维矩阵时同样如此）

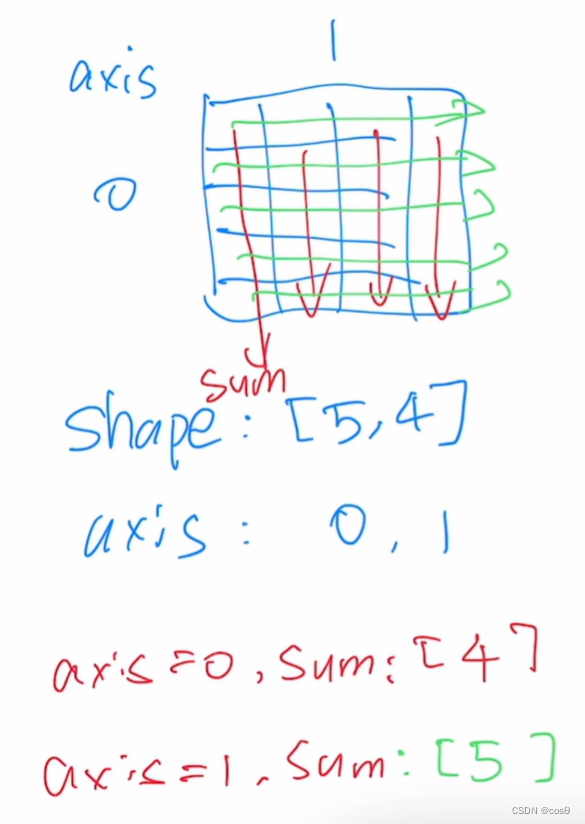
A.sum(axis=[0, 1])  # SameasA.sum()

tensor(190.)

在这里，sum(axis=[0,1])怎么求? 求和为顺序先0, 后1

再举一个高维数组的例子

B = torch.arange(40).reshape(-1,5,4)
B.shape,B.sum(),B

(torch.Size([2, 5, 4]),
 tensor(780),
 tensor([[[ 0,  1,  2,  3],
          [ 4,  5,  6,  7],
          [ 8,  9, 10, 11],
          [12, 13, 14, 15],
          [16, 17, 18, 19]],
 
         [[20, 21, 22, 23],
          [24, 25, 26, 27],
          [28, 29, 30, 31],
          [32, 33, 34, 35],
          [36, 37, 38, 39]]]))

B0 = B.sum(axis = 0)
B0,B0.shape

(tensor([[20, 22, 24, 26],
         [28, 30, 32, 34],
         [36, 38, 40, 42],
         [44, 46, 48, 50],
         [52, 54, 56, 58]]),
 torch.Size([5, 4]))

B1 = B.sum(axis = 1)
B1,B1.shape

(tensor([[ 40,  45,  50,  55],
         [140, 145, 150, 155]]),
 torch.Size([2, 4]))

B.sum(axis = [1,2]).shape

torch.Size([2])

非降维求和

有时在调用函数来计算总和或均值时保持轴数不变会很有用。

sum_A = A.sum(axis=1, keepdims=True)#保证一个二维数组仍然是二维数组，虽然行/列数会变化
sum_A,sum_A.shape

(tensor([[ 6.],
         [22.],
         [38.],
         [54.],
         [70.]]),
 torch.Size([5, 1]))

例如，由于sum_A在对每行进行求和后仍保持两个轴，我们可以通过广播将A除以sum_A

#例如，由于sum_A在对每行进行求和后仍保持两个轴，我们可以通过广播将A除以sum_A。
A / sum_A

tensor([[0.0000, 0.1667, 0.3333, 0.5000],
        [0.1818, 0.2273, 0.2727, 0.3182],
        [0.2105, 0.2368, 0.2632, 0.2895],
        [0.2222, 0.2407, 0.2593, 0.2778],
        [0.2286, 0.2429, 0.2571, 0.2714]])

如果我们想沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），我们可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。

#如果我们想沿某个轴计算A元素的累积总和， 比如axis=0（按行计算），我们可以调用cumsum函数。 此函数不会沿任何轴降低输入张量的维度。
A.cumsum(axis=0)

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  6.,  8., 10.],
        [12., 15., 18., 21.],
        [24., 28., 32., 36.],
        [40., 45., 50., 55.]])

3. 点积

给定两个向量$x,y\in {\mathbb{R}}^d$， 它们的点积（dot product）$x^{T}y$ （或$<x,y>$） 是相同位置的按元素乘积的和：$x^{T}y={\sum }_{i=1}^d{x}_i{y}_i$。

torch.dot()函数是用于向量乘向量的函数

#点积
x = torch.arange(4,dtype = torch.float32)
y = torch.ones(4, dtype = torch.float32)

x, y, torch.dot(x, y)

(tensor([0., 1., 2., 3.]), tensor([1., 1., 1., 1.]), tensor(6.))

4. 矩阵-向量积

在代码中使用张量表示矩阵-向量积，我们使用与点积相同的mv函数。 当我们为矩阵A和向量x调用torch.mv(A, x)时，会执行矩阵-向量积。 注意，A的列维数（沿轴1的长度）必须与x的维数（其长度）相同。

#矩阵-向量积
A.shape, x.shape, torch.mv(A, x)

(torch.Size([5, 4]), torch.Size([4]), tensor([ 14.,  38.,  62.,  86., 110.]))

5. 矩阵-矩阵乘法

torch.mm()是用于矩阵乘矩阵的函数

#矩阵-矩阵乘法
C = torch.ones(4, 3)
torch.mm(A,C)

tensor([[ 6.,  6.,  6.],
        [22., 22., 22.],
        [38., 38., 38.],
        [54., 54., 54.],
        [70., 70., 70.]])

6. 范数

u = torch.tensor([3.0, -4.0])
torch.norm(u)

tensor(5.)

torch.abs(u).sum()

tensor(7.)

torch.norm(torch.ones((4, 9)))

tensor(6.)

在深度学习中，我们经常试图解决优化问题： 最大化分配给观测数据的概率; 最小化预测和真实观测之间的距离。 用向量表示物品（如单词、产品或新闻文章），以便最小化相似项目之间的距离，最大化不同项目之间的距离。 目标，或许是深度学习算法最重要的组成部分（除了数据），通常被表达为范数。

最后

以上就是漂亮路灯为你收集整理的Python中线性代数的相关基础知识1. 张量算法的基本性质2. 降维3. 点积4. 矩阵-向量积5. 矩阵-矩阵乘法6. 范数的全部内容，希望文章能够帮你解决Python中线性代数的相关基础知识1. 张量算法的基本性质2. 降维3. 点积4. 矩阵-向量积5. 矩阵-矩阵乘法6. 范数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。