【深入剖析】彻底弄明白十进制----＞n进制转换

前言

记录进制转换相关问题
不说废话，直接进入正文

正文

10进制转换为8/16进制的通用办法：10 --> 2 --> 8/16

10 —> 2

正整数

步骤：短除法 ，余数倒着取即为二进制数

举例：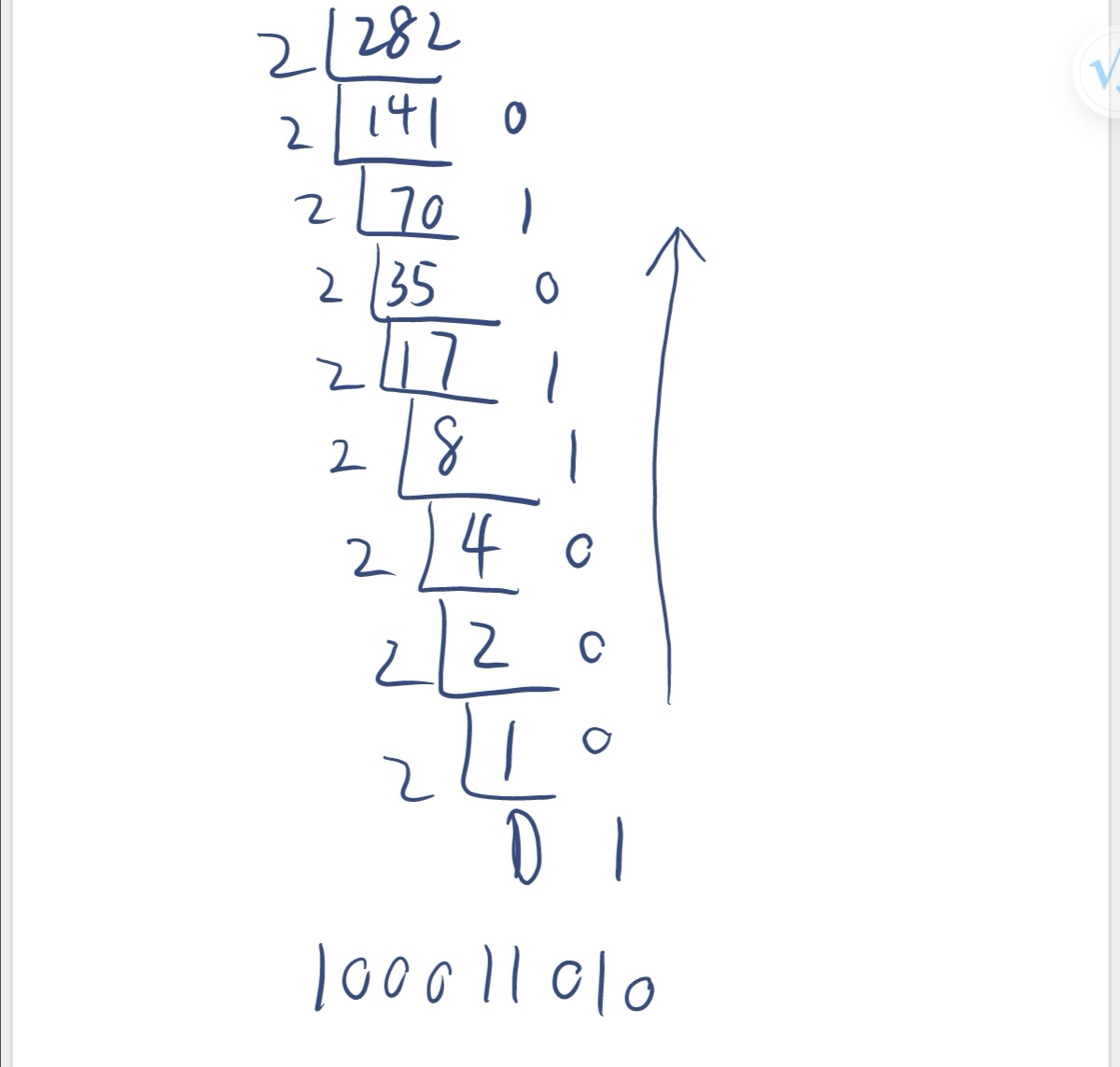
所以282的二进制数就是 100011010

负整数

步骤：先用短除法求对应正数的二进制数，按位取反，整体+1

举例：例如求 -282 的二进制数
先求 282 的二进制数
1 0 0 0 1 1 0 1 0 （282的二进制数）
0 1 1 1 0 0 1 0 1 （按位取反）
0 1 1 1 0 0 1 1 0 （按二进制的加法运算方式，整体的值+ 1）

正小数（无整数部分）

步骤：整体乘2，取出结果整数位即为这个小数的二进制数的第一位。取出结果的小数部分继续乘二，将第二次的结果的整数部分取出来，就是这个小数的二进制数的第二位，以此类推

举例：求 0.75 的二进制数

结果为 0.110

负小数（无整数部分）

步骤：负号只影响整数，不影响小数部分，只计算对应的正小数即可

举例：求 - 0.75 的二进制数
结果同上：0.110

综合起来

步骤：将整数和小数部分拼接到一起

举例：求 -282.75 的二进制

把上面的结果拿下来，拼到一起，结果： 0 1 1 1 0 0 1 1 0 . 1 1 0

2 —> 8

步骤：每隔三位算一组，不足三个补0凑满三位，每一组求出对应值

举例：求 100011010.11 的八进制
100 011 010 . 110 （补零）
100 011 010 . 110 （分组）
4 3 2 . 6 （每一组求对应值）

结果：432.6

2 —> 16

步骤：每隔四位算一组，不足四个补0凑满四位，每一组求出对应值

举例：求 100011010.11 的十六进制
1001 0001 1010. 1100 （补零,补足正负号）
1001 0001 1010. 1100 （分组）
-1 1 a . c

结果： -11a.c

结尾

记录一下计算过程，方便查找

最后

以上就是害羞星月为你收集整理的【深入剖析】彻底弄明白十进制----＞n进制转换的全部内容，希望文章能够帮你解决【深入剖析】彻底弄明白十进制----＞n进制转换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。