MATLAB数字滤波器设计 IIR（冲激响应不变法、双线性变换法）、FIR

77 阅读 0 评论 51 点赞

我是靠谱客的博主火星上学姐，最近开发中收集的这篇文章主要介绍MATLAB数字滤波器设计 IIR（冲激响应不变法、双线性变换法）、FIR，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1．分别利用冲激响应不变法和双线性变换法设计巴特沃斯低通滤波器

2．巴特沃斯高通滤波器设计

3. FIR滤波器设计

1．分别利用冲激响应不变法和双线性变换法设计巴特沃斯低通滤波器

　　要求：通带截止频率几fp=200Hz，阻带截止频率fs=400Hz，δp=1dB，δs=30dB，抽样间隔T=1ms。

clc;clear;close;

% 数字滤波器的技术指标要求

ap=1;as=30;fp=200;fs=400;

Fs=1000;

% 采用冲激响应不变法

% 给定的模拟频率转模拟角频率

wap=2*pi*fp;

was=2*pi*fs;

% 设计模拟滤波器

[N,wac]=buttord(wap,was,ap,as,'s');  % N为阶数，wac为3dB截止频率

[z,p,k]=buttap(N);     % 创建巴特沃斯低通滤波器 z零点p极点k增益

[Bap,Aap]=zp2tf(z,p,k);% 由零极点和增益确定归一化Han(s)系数

[Bbs,Abs]=lp2lp(Bap,Aap,wac);     % 低通到低通 计算去归一化Ha(s)

[B,A]=impinvar(Bbs,Abs,Fs);       % 模拟域到数字域

[H1,w]=freqz(B,A);               % 根据H(z)求频率响应特性

% 绘制数字滤波器频响幅度谱

figure(1);

f=w*Fs/(2*pi);

subplot(211);

plot(f,20*log10(abs(H1)));          % 绘制幅度响应

xlabel('频率/Hz');

ylabel('H1幅值/dB');

subplot(212);

plot(f,unwrap(angle(H1)));          % 绘制相位响应

xlabel('频率/Hz');

ylabel('角度/Rad');



% 采用双线性变换法

% 给定的模拟频率转数字频率

wp=(2*pi*fp)/Fs

ws=(2*pi*fs)/Fs

% 数字指标转模拟指标 预畸变

wap=2*tan(wp/2)*Fs;

was=2*tan(ws/2)*Fs;

% 设计模拟滤波器

[N,wac]=buttord(wap,was,ap,as,'s');  % N为阶数，wac为3dB截止频率

[z,p,k]=buttap(N);     % 创建巴特沃斯低通滤波器 z零点p极点k增益

[Bap,Aap]=zp2tf(z,p,k);% 由零极点和增益确定归一化Han(s)系数

[Bbs,Abs]=lp2lp(Bap,Aap,wac);    % 低通到低通 计算去归一化Ha(s)

[B,A] = bilinear(Bbs,Abs,Fs);      % 模拟域到数字域

[H1,w] = freqz(B,A);             % 根据H(z)求频率响应特性

% 绘制数字滤波器频响幅度谱

figure(2);

f=w*Fs/(2*pi);

subplot(211);

plot(f,20*log10(abs(H1)));          % 绘制幅度响应

xlabel('频率/Hz');

ylabel('H1幅值/dB');

subplot(212);

plot(f,unwrap(angle(H1)));          % 绘制相位响应

xlabel('频率/Hz');

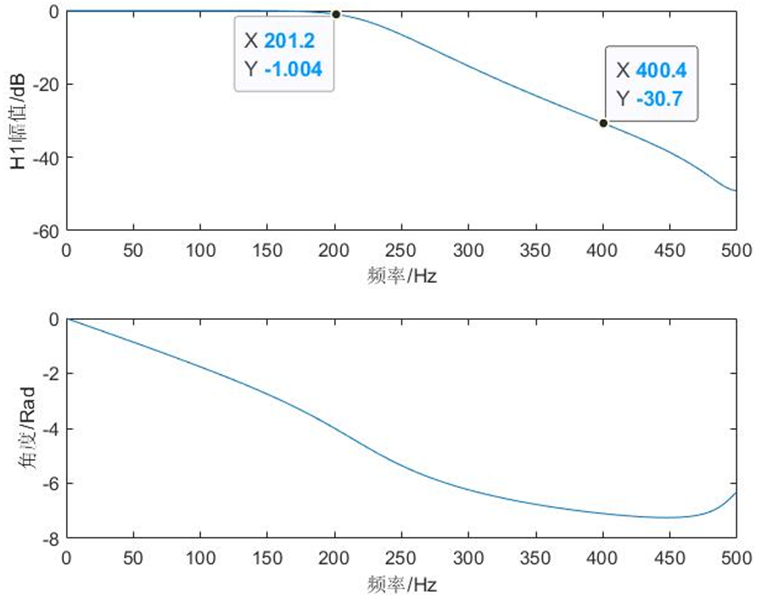
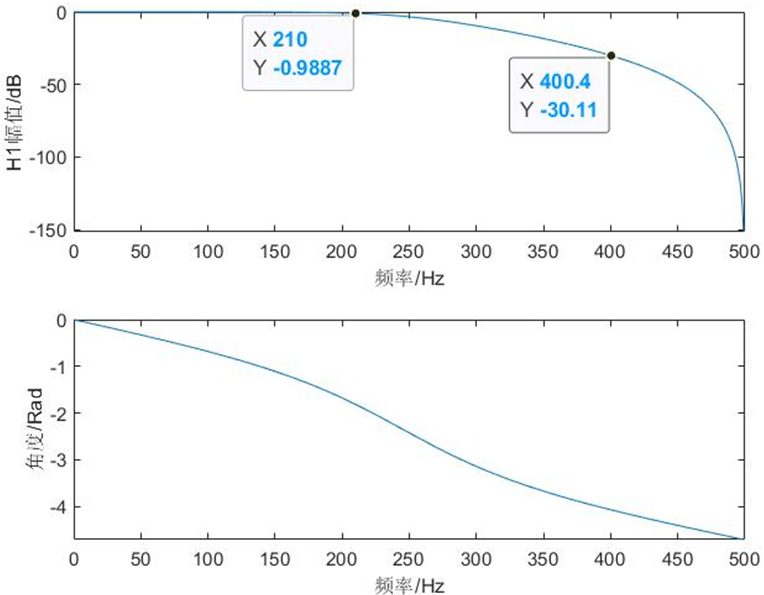
ylabel('角度/Rad');

　　冲激响应不变法设计的巴特沃斯低通滤波器的幅度响应和相位响应如（图1.1），双线性变换法设计的巴特沃斯低通滤波器的幅度响应和相位响应如（图1.2）。

　　冲激响应不变法通过单位冲激响应逼近原模拟滤波器的单位冲激响应，时域特性逼近很好，且模拟域和数字域的转换是线性的。双线性变换法模拟域与数字域转换是非线性的，存在失真的情况，但其克服了多值映射，可消除频谱混叠。

2．巴特沃斯高通滤波器设计

　　要求：通带截止频率fp=200Hz，阻带截止频率fs=100Hz，幅度特性单调下降，fp处最大衰减为3dB，阻带最小衰减15dB。

　　高通滤波器只能采用双线性变换法进行设计，代码如下。

clc;clear;close;

% 采用双线性变换法

% 数字滤波器的技术指标要求

ap=3;as=15;fp=200;fs=100;

Fs=1000;

% 给定的模拟频率转数字频率

wp=(2*pi*fp)/Fs

ws=(2*pi*fs)/Fs

% 数字指标转模拟指标 预畸变

wap=2*tan(wp/2)*Fs;

was=2*tan(ws/2)*Fs;

% 设计模拟滤波器

[N,wac]=buttord(wap,was,ap,as,'s');     % N为阶数，wac为3dB截止频率

[z,p,k]=buttap(N);     % 创建巴特沃斯低通滤波器 z零点p极点k增益

[Bap,Aap]=zp2tf(z,p,k);% 由零极点和增益确定归一化Han(s)系数

[Bbs,Abs]=lp2hp(Bap,Aap,wac);     % 低通到高通 计算去归一化Ha(s)

[B,A]=bilinear(Bbs,Abs,Fs);        % 模拟域到数字域

[H1,w]=freqz(B,A);               % 根据H(z)求频率响应特性

% 绘制数字滤波器频响幅度谱

f=w*Fs/(2*pi);

subplot(211);

plot(f,20*log10(abs(H1)));          % 绘制幅度响应

xlabel('频率/Hz');

ylabel('H1幅值/dB');

subplot(212);

plot(f,unwrap(angle(H1)));          % 绘制相位响应

xlabel('频率/Hz');

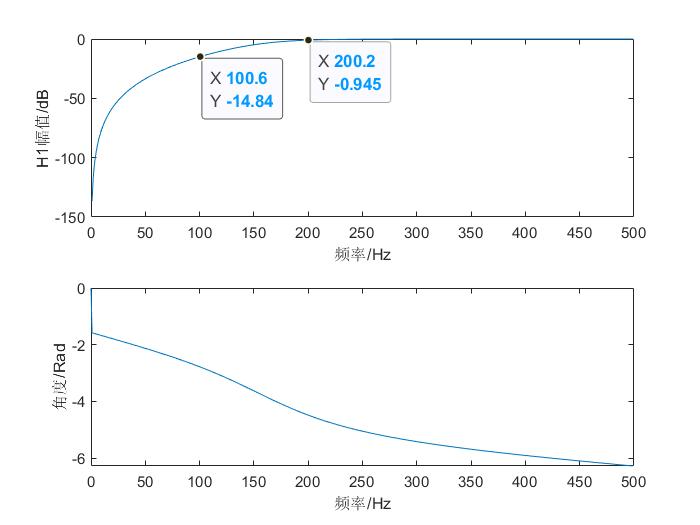
ylabel('角度/Rad');

　　运行上述代码，得到使用双线性变换法设计的巴特沃斯高通滤波器的幅度响应和相位响应图，如（图2.1）。

3. FIR滤波器设计

要求：通带截止频率为350Hz，阻带截止频率为500Hz，阻带最小衰减40dB。

　　采用汉宁窗，MATLAB代码如下。

% 数字滤波器的技术指标要求
fp=350;fs=500;
Fs=6000;
% 模拟频率转数字频率
wp=2*pi*fp/Fs;
ws=2*pi*fs/Fs;
% 计算截止频率wc和群时延alfa
wc=(wp+ws)/2;                     % 计算截止频率
deltaw=ws-wp;                     % 过渡带宽度
N0=ceil(3.1*2*pi/deltaw);            % 查表计算阶数 采用汉宁窗
N=N0+mod(N0+1, 2);               % N为奇数
alfa=(N-1)/2;                      % 群时延
% 计算理想低通滤波器的单位冲激响应hd(n)
n=0:N-1;
hd=sin(wc*(n-alfa+eps))./(pi*(n-alfa+eps));
windows=(hanning(N))';             % 生成汉宁窗 窗函数
B=hd.*windows;                   % 获得FIR滤波器单位冲激响应
[H1,w]=freqz(B,1);
% 保存滤波器系数为MAT文件
A=1;
save('FIRFilter.mat','B','A');
% 绘制数字滤波器频响幅度谱
figure(1);
f=w*Fs/(2*pi);
subplot(211);
plot(f,20*log10(abs(H1)));          % 绘制幅度响应
xlabel('频率/Hz');
ylabel('H1幅值/dB');
subplot(212);
plot(f,unwrap(angle(H1)));          % 绘制相位响应
xlabel('频率/Hz');
ylabel('角度/Rad');

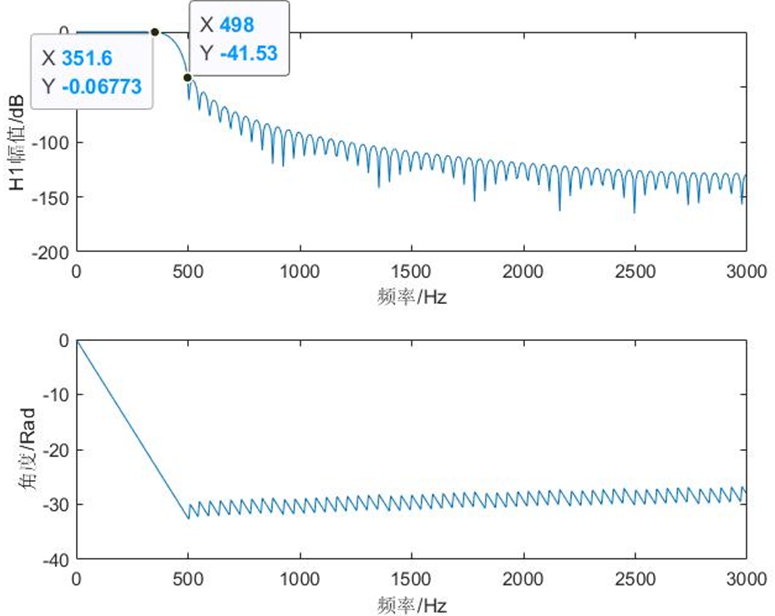
　　设计的滤波器幅频特性和相频特性如（图3.1）。设计的滤波器满足指标要求，且具有很好的线性相位，信号通过该滤波器不会产生失真。