概述
【 1. 差分与差分方程】
1. 差分
一
阶
向
后
差
分
：
▽
f
(
k
)
=
f
(
k
)
−
f
(
k
−
1
)
一阶向后差分：▽f(k)=f(k)-f(k-1)
一阶向后差分：▽f(k)=f(k)−f(k−1)
2. 差分方程
例：
【 2. 差分方程的经典解】
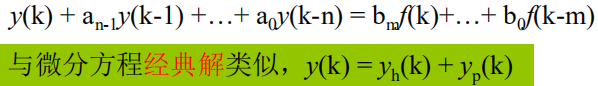
1. 求齐次方程的齐次解
- 特征根：
- 齐次解:
2. 求特解
- 根据激励形式选特解形式：
【 3. 零输入响应、零状态响应 】
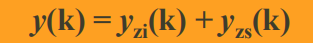
- 零输入相应：
- 零状态响应：
- 例：
【 4. 总结 】
- 求零输入响应步骤：
①通过递归求出初始值。
①令输入为0，根据特征方程求出特征根，写出齐次解的形式。
②将初始值待入齐次解，求得系数。 - 求零状态响应步骤：
①递归求得初始值。
②求出其特征方程对应的特征根，得到齐次解。
③通过激励确定特解的形式，带入零状态方程，得到特解。
④将初始值待入到齐次解+特解=通解的方程中，求得系数。
最后
以上就是愤怒电源为你收集整理的【离散系统的时域分析】1. 离散系统的响应【 1. 差分与差分方程】【 2. 差分方程的经典解】【 3. 零输入响应、零状态响应 】【 4. 总结 】的全部内容，希望文章能够帮你解决【离散系统的时域分析】1. 离散系统的响应【 1. 差分与差分方程】【 2. 差分方程的经典解】【 3. 零输入响应、零状态响应 】【 4. 总结 】所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复