描述

我有一个点集，里面都是[x,y]这样的二维点，这个点集能形成一个曲线。
在并不想去求这个曲线的表达式时，怎么得到某一点的曲率呢

相关知识

曲率的定义是：
针对曲线上某个点的切线方向角对弧长的转动率，而曲率的倒数就是曲率半径
$$K=\left|\frac{\Delta \theta }{l}\right|=\left|\frac{1}{r}\right|$$

式子中$K$代表的就是曲率，$\Delta \theta$代表的就是切线方向角的变化，$l$代表弧长，$r$代表的就是曲率半径

式子也挺好看懂的。我们都知道圆的周长是$2\pi r$，任意一段弧长 的计算方式是
$$l=\theta \cdot r$$

式子中的$\theta$代表的就是弧长对应的角度

解决

我有一段圆弧ab，对应的圆内角$\theta$是啥我不用解释了吧，初中数学

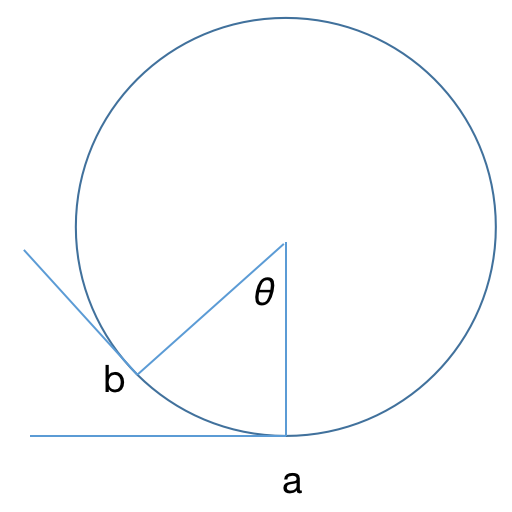
那么到这儿也比较简单了，如果离散点中，ab就是相邻的两个点，那么a点（或者b点或者随便哪个点）的曲率怎么计算呢

我们设要求的点 $p$，在点集 $P$ 的位置是 $i$ ，点集实际上是 $0$ 到 $n$ 的一系列二维点，那么点p的曲率$K_i$的表达式是
$$K_i=\left|\frac{\arctan \left(\frac{y_{i+2}-y_{i+1}}{x_{i+2}-x_{i+1}}\right)-\arctan \left(\frac{y_{i+1}-y_i}{x_{i+1}-x_i}\right)}{\sqrt{{\left(x_{i+1}-x_i\right)}^2+{\left(y_{i+1}-y_i\right)}^2}}\right|$$

挺好理解的，下面的是两点之间的距离，上面是切线方向角之差，不解释啦

补充

上面计算方式写的很清楚了，但其实有个小小问题
假设我有100个点，按照上面的公式，第1个点到第98个点都是可以很快计算出来的。

但99个点和100个点，因为没有101和102两个点，这两个点的曲率是无法计算的。

解决办法也很简单：

• 我使用离散点曲率计算，主要是在路径规划当中使用，我的这个离散点集在最后两个点上，实际上可以认为是路径终点，需要轨迹很平滑的。我的操作就是，将最后两个点的曲率，赋值成了倒数第三个点一样，问题应该不大。你可以根据自己的需求任意设置。
• 如果你就是不想自己设定，非要计算的来。造102个点，使用前100个，造n+2个点，使用前n个。（挺无聊的解决办法哈）

最后

以上就是害羞方盒为你收集整理的离散点的曲率计算描述相关知识解决补充的全部内容，希望文章能够帮你解决离散点的曲率计算描述相关知识解决补充所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。