空域滤波算法对比分析（超级全面哒）——Python代码

90 阅读 0 评论 60 点赞

我是靠谱客的博主满意康乃馨，最近开发中收集的这篇文章主要介绍空域滤波算法对比分析（超级全面哒）——Python代码，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

代码包括椒盐噪声，高斯噪声，均值滤波，中值滤波，高斯滤波，Sobel滤波，Laplace滤波和对应的系统函数以及三种常用的参数分析，MSE，PSNR，SSIM。

太久没写博客了，懒得把知识点都写下来，有缘人看到需要报告的移步传送门去下载报告，报告上写的很详细。

图5 原图与取灰度值后的图片

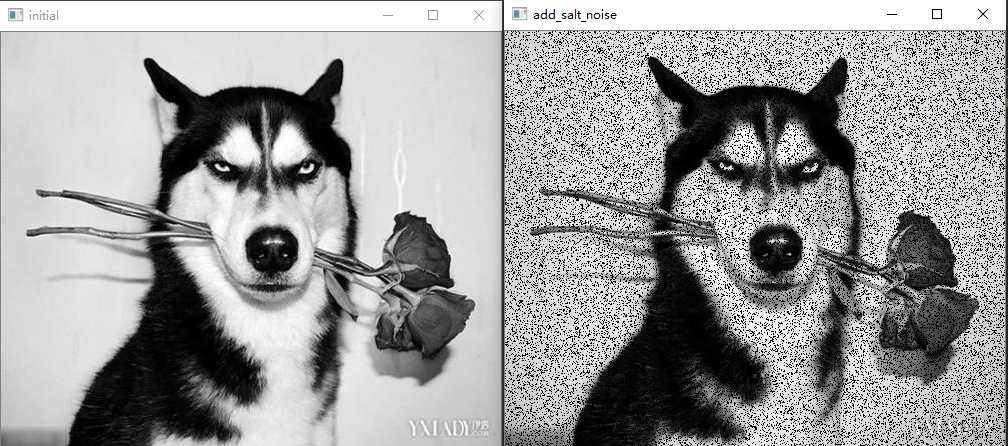
图6 原图加信噪比0.2的椒盐噪声

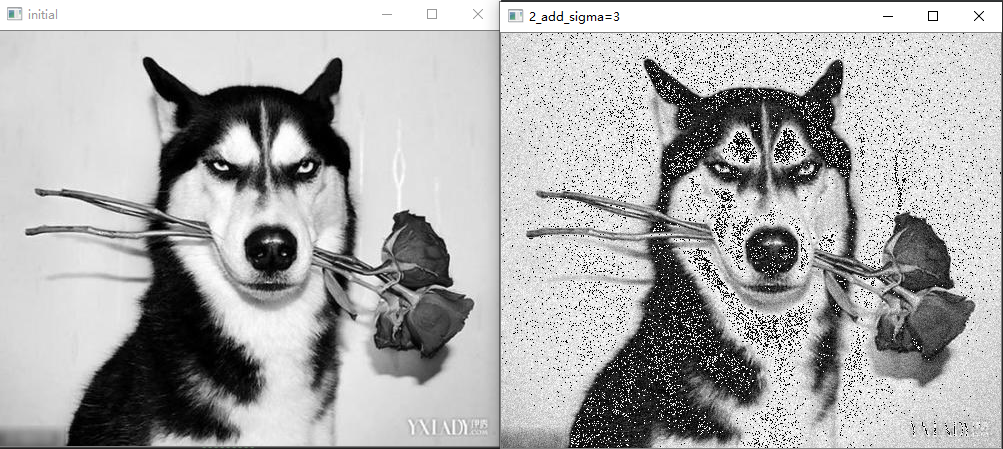
图7原图加sigma=3的高斯噪声

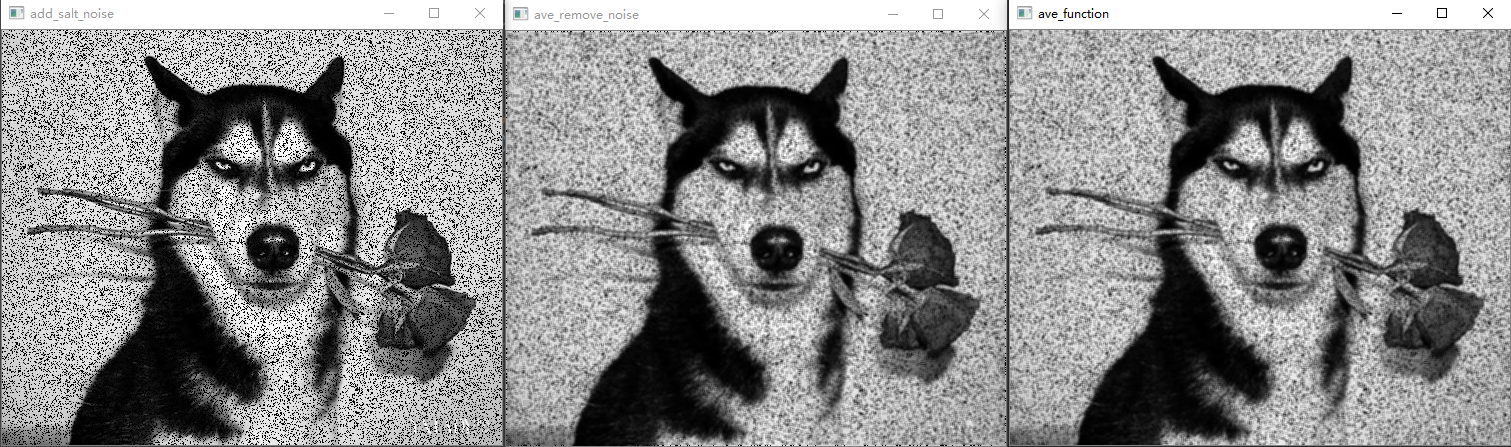
图8 椒盐噪声，3*3均值滤波，系统3*3均值滤波

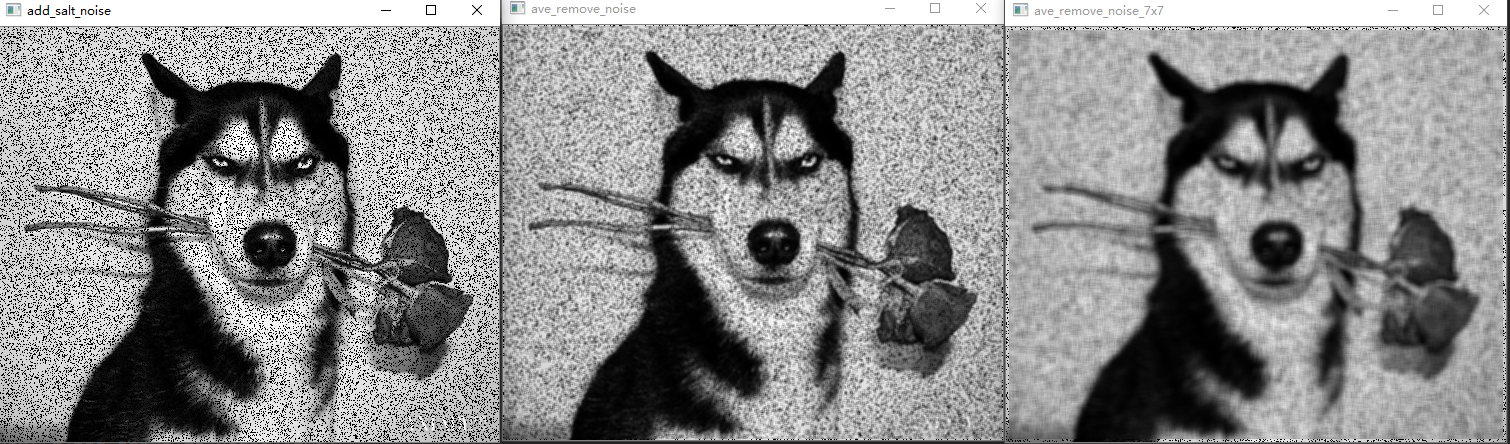
图9椒盐噪声，3*3均值滤波，7*7均值滤波

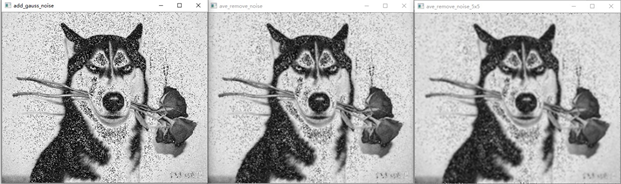
图10 高斯噪声，3*3均值滤波，5*5均值滤波

高斯滤波（加权均值滤波）：

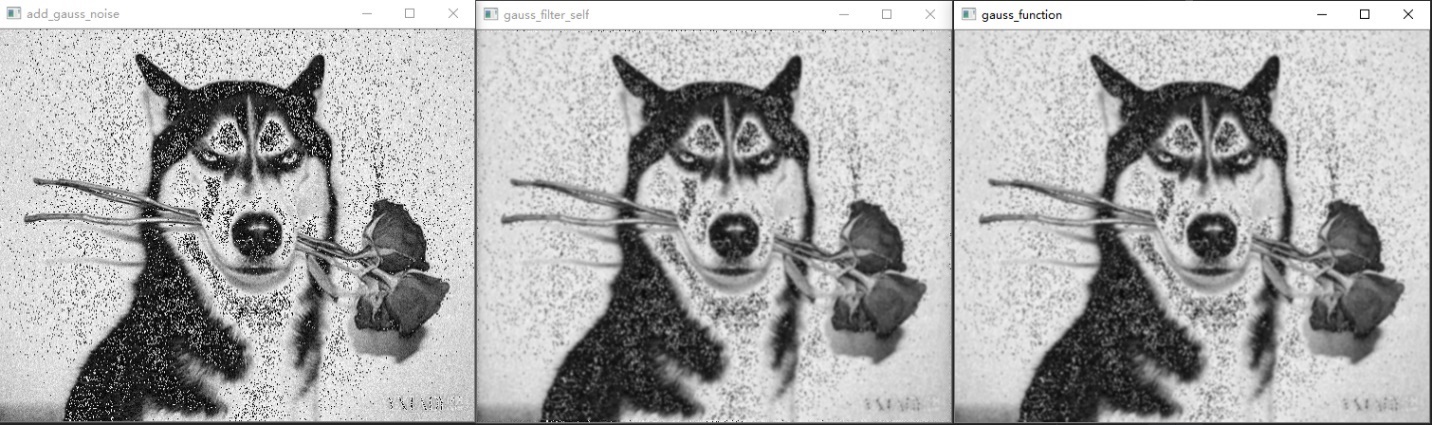
图11 高斯噪声，5*5高斯滤波，5*5系统高斯滤波

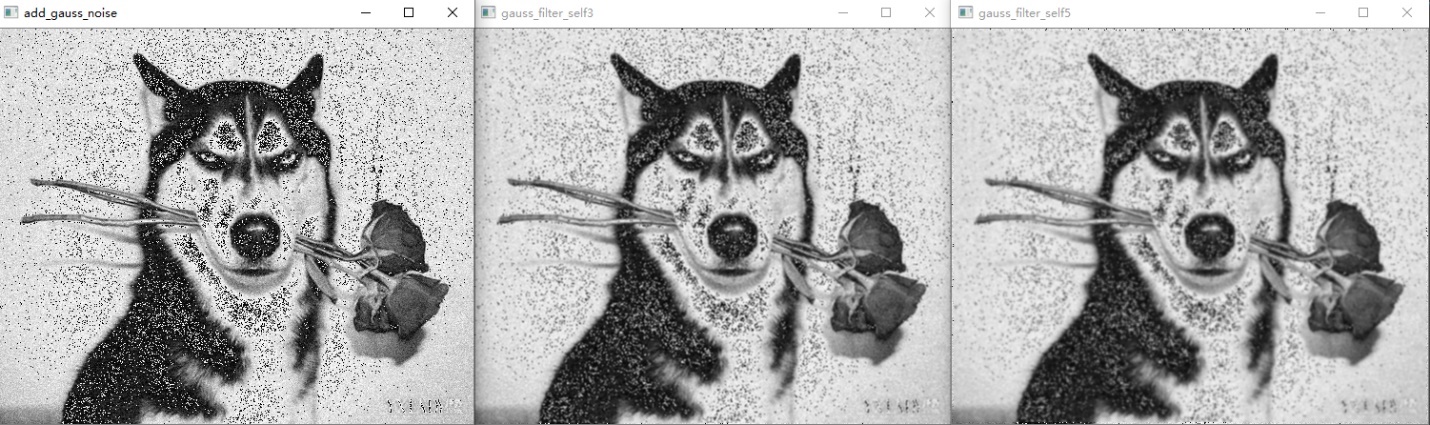
图12 高斯噪声，3*3高斯滤波，5*5高斯滤波

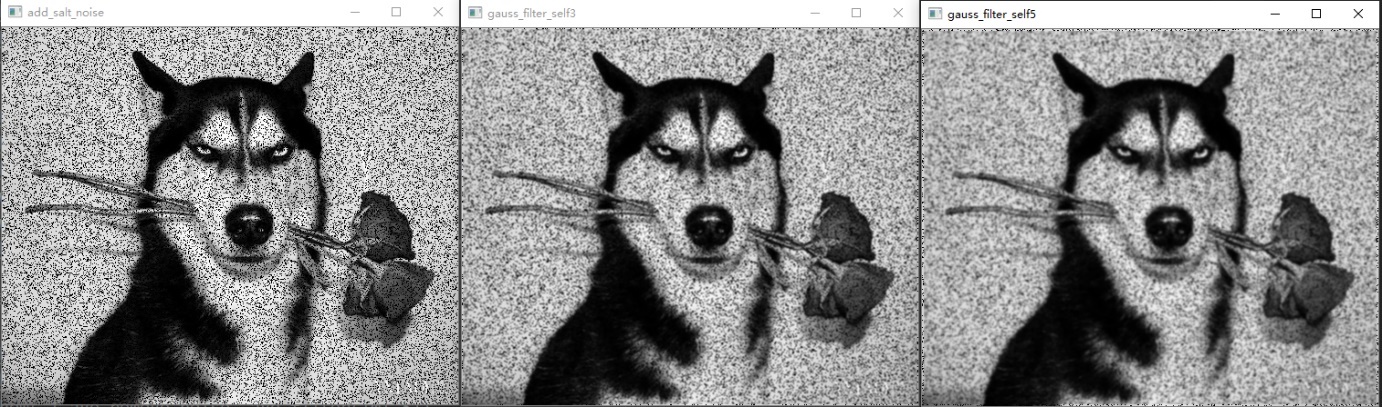
图13 椒盐噪声，3*3高斯滤波，5*5高斯滤波

中值滤波：

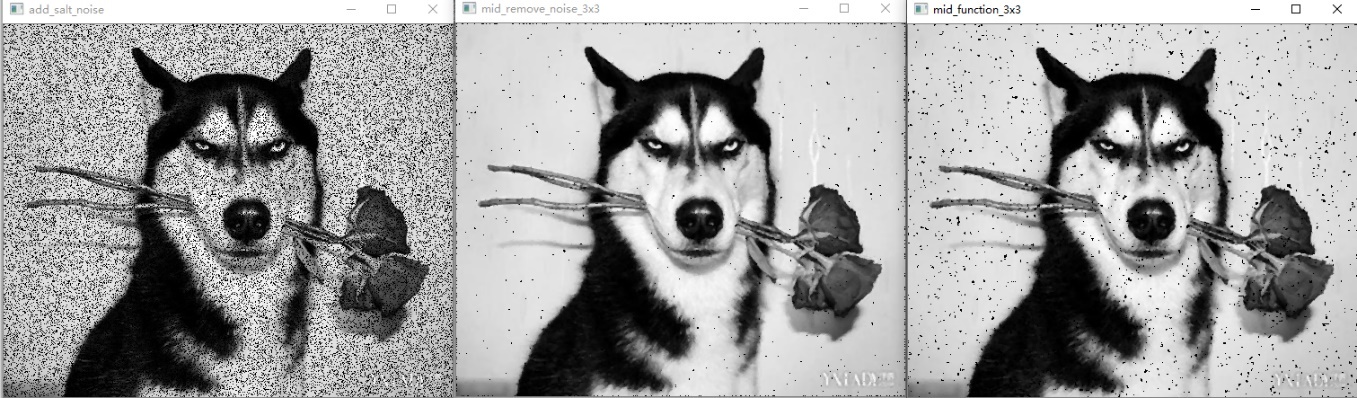
图15 椒盐噪声，3*3中值滤波，3*3系统中值滤波

16 椒盐噪声，3*3中值滤波，5*5中值滤波 10*10中值滤波

Sobel算子滤波：

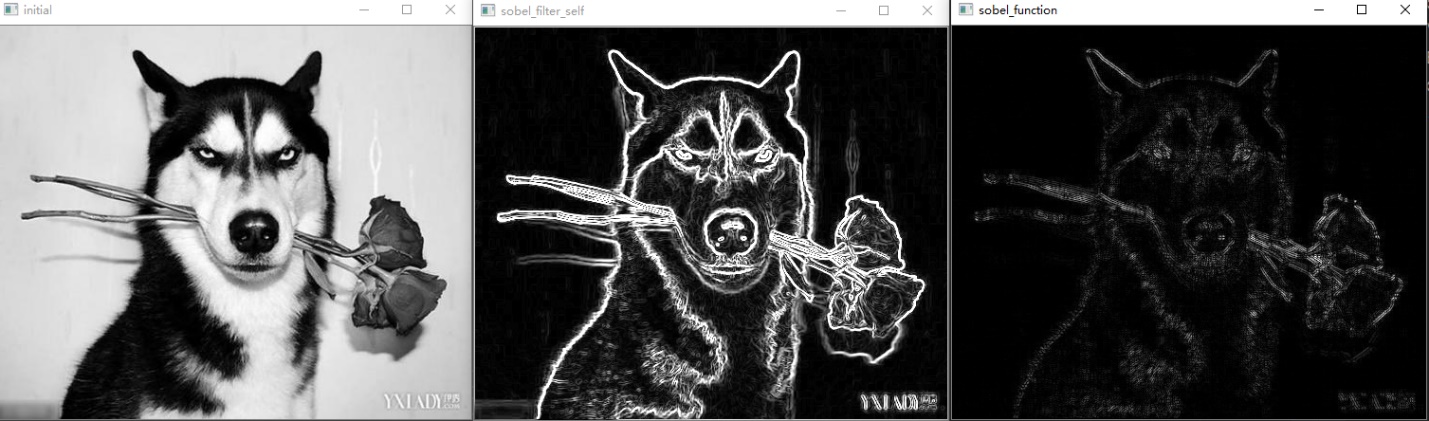
图17 原图，Sobel滤波，系统Sobel滤波

Laplace滤波：

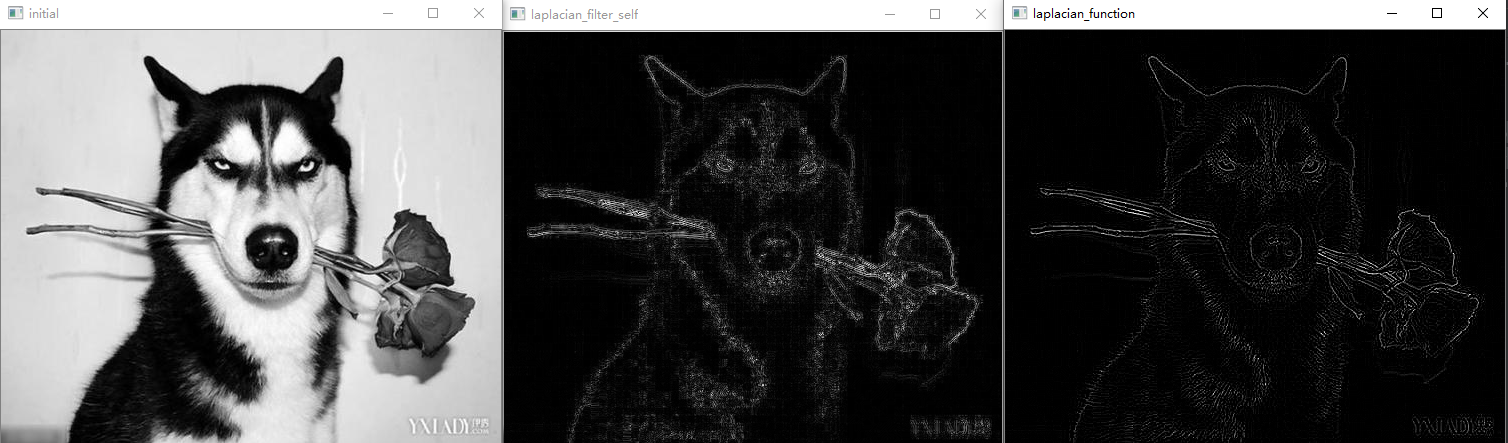
图18 原图，Laplace滤波，系统Laplace滤波

#########所有函数###################
Mse 两个图片均方差
Psnr 两个图片峰值信噪比
Ssim 两个图片相似度
matrix_convolve 两矩阵卷积
add_salt_noise 加椒盐噪声
add_gauss_noise	加高斯噪声
get_mid	取矩阵均值
get_ave 取矩阵中位数
mid_filter 中值滤波
mid_function 系统中值滤波函数
ave_filter 均值滤波
ave_function 系统均值滤波函数
gauss_filter_self 高斯滤波
gauss_function 系统高斯滤波函数
sobel_filter_self
Sobel算子锐化
sobel_function
系统Sobel算子锐化
laplacian_filter_self 拉普拉斯算子锐化
laplacian_function 系统拉普拉斯算子锐化
#######################################
import cv2 as cv
import numpy as np
import random
import math
import copy
###########均方误差(MSE)###########
def mse(pc1,pc2):
mse=np.mean((pc1-pc2)**2)
return float(mse)
###########峰值信噪比(PSNR)##########
# PSNR高于40dB说明图像质量极好（即非常接近原始图像）
# 在30—40dB通常表示图像质量是好的（即失真可以察觉但可以接受）
# 在20—30dB说明图像质量差
# 最后 PSNR低于20dB图像不可接受
def psnr(img1, img2):
mse = np.mean( (img1 - img2) ** 2 )
if mse == 0:
return 100
plxel_max = 255.0
return 20 * math.log10(plxel_max / math.sqrt(mse))
###########结构相似度(SSIM):range~[-1:1]##########
#-1表示完全不相似,1表示完全相似
def ssim(y_true, y_pred):
u_true = np.mean(y_true)
u_pred = np.mean(y_pred)
var_true = np.var(y_true)
var_pred = np.var(y_pred)
std_true = np.sqrt(var_true)
std_pred = np.sqrt(var_pred)
c1 = np.square(0.01 * 7)
c2 = np.square(0.03 * 7)
ssim = (2 * u_true * u_pred + c1) * (2 * std_pred * std_true + c2)
denom = (u_true ** 2 + u_pred ** 2 + c1) * (var_pred + var_true + c2)
return ssim / denom
###############矩阵卷积##############
def matrix_convolve(pc,mode):
n,m=pc.shape
c=np.zeros((n,m),dtype=np.float)
step=mode.shape[0]
mode=mode/mode.sum()
# 除于加权平均
for i in range(n):
for j in range(m):
if i-int(step/2)<0 or i+int(step/2)>=n:
c[i][j]=pc[i][j]
elif j-int(step/2)<0 or j+int(step/2)>= m:
c[i][j]=pc[i][j]
else:
x=int(step/2)
c[i][j]=np.sum(pc[i-x:i-x+step,j-x:j-x+step]*mode)
c=c.clip(0,255)
c=cv.convertScaleAbs(c) #将结果转化为8位int
return c
###############加椒盐噪声################
def add_salt_noise(pc,maybe):#图片,噪声比
n,m=pc.shape
for i in range(n):
for j in range(m):
if np.random.random(1)>maybe:
continue
else:
pc[i,j]=0
###############加高斯噪声################
def add_gauss_noise(pc,mu,sigma,k,maybe=1):#means 均值 sigma 方差
n,m=pc.shape
for i in range(n):
for j in range(m):
if np.random.random(1)<=maybe:
pc[i][j]+=k*random.gauss(mu,sigma)
pc[i][j]=min(pc[i][j],255)
pc[i][j]=max(pc[i][j],0)
##############求中值##############
def get_mid(pc,x,y,cnt):
ans=[]
for i in range(x-int(cnt/2),x+int(cnt/2)+1):
for j in range(y-int(cnt/2),y+int(cnt/2)+1):
ans.append(pc[i][j])
ans.sort()
return ans[int(len(ans)/2)+1]
##############求均值##############
def get_ave(pc,x,y,cnt):
ans=0
for i in range(x-int(cnt/2),x+int(cnt/2)+1):
for j in range(y-int(cnt/2),y+int(cnt/2)+1):
ans+=pc[i][j]
return int(ans/cnt/cnt)
############中值滤波#############
def mid_filter(pc,step): #图片,几位滤波
n,m=pc.shape
c=np.zeros((n,m),dtype="uint8")
for i in range(0,n):
for j in range(0,m):
if i-int(step/2)<0 or i+int(step/2)>=n:
c[i][j]=pc[i][j]
elif j-int(step/2)<0 or j+int(step/2)>=m:
c[i][j]=pc[i][j]
else:
c[i][j]=get_mid(pc,i,j,step)
return c
def mid_function(pc,step):
c=cv.medianBlur(pc,step)
return c
############均值滤波#############
def ave_filter(pc,step):
n,m=pc.shape
c = np.zeros((n, m), dtype="uint8")
for i in range(n):
for j in range(m):
if i - int(step / 2) < 0 or i + int(step / 2) >= n:
c[i][j] = pc[i][j]
elif j - int(step / 2) < 0 or j + int(step / 2) >= m:
c[i][j] = pc[i][j]
else:
c[i][j] = get_ave(pc,i,j,step)
return c
def ave_function(pc,step):
c=cv.blur(pc,(step,step))
return c
###########高斯平滑#############
def gauss_filter_self(pc,step):
if step==3:
mode=np.array([[1,2,1],[2,4,2],[1,2,1]])
if step==5:
mode=np.array([[1,4,7,4,1],[4,16,26,16,4],[7,26,41,26,7],[4,16,26,16,4],[1,4,7,4,1]])
return matrix_convolve(pc,mode)
def gauss_function(pc,step):
c=cv.GaussianBlur(pc,(step,step),0)
return c
###########Sobel###############
#sobel算子
# Gx =-1 0 1
Gy =1 2 1
#
-2 0 2
0 0 0
#
-1 0 1
-1-2-1
def sobel_filter_self(pc):
c=copy.deepcopy(pc)
n,m=pc.shape
for i in range(1,n-1):
for j in range(1,m-1):
x=int(pc[i+1,j+1])-int(pc[i-1,j+1])+int(pc[i+1,j-1])-int(pc[i-1,j-1])+int(2*pc[i+1,j])-int(2*pc[i-1,j])
y=int(pc[i+1,j+1])-int(pc[i+1,j-1])+int(pc[i-1,j+1])-int(pc[i-1,j-1])+int(2*pc[i,j+1])-int(2*pc[i,j-1])
c[i,j]=min(255,int(math.sqrt(x*x+y*y)))
c=cv.convertScaleAbs(c)
return c
def sobel_function(pc):
edges=cv.Sobel(pc,cv.CV_16S,1,1)
edgesh=cv.convertScaleAbs(edges)
return edgesh
###########Laplacian###############
#Laplacian算子
# 0
1
0
# 1 -4
1
# 0
1
0
def laplacian_filter_self(pc):
c=copy.deepcopy(pc)
n,m=pc.shape
for i in range(1,n-1):
for j in range(1,m-1):
c[i,j]=abs(int(pc[i+1,j])+int(pc[i-1,j])+int(pc[i,j-1])+int(pc[i,j+1])-int(4*pc[i,j]))
c[i,j]=min(255,c[i,j])
c=cv.convertScaleAbs(c)
return c
def laplacian_function(pc):
edges=cv.Laplacian(pc,-1)
return edges
################################
begin=cv.imread('E:/PC/4.jpg')
im=cv.imread('E:/PC/4.jpg',0) #读取图片并取灰度值
cv.imshow("begin",begin)
a=copy.deepcopy(im)
b=copy.deepcopy(im)
cv.imshow("initial",im) #输入图片
add_salt_noise(im,0.2) #椒盐噪声
add_gauss_noise(im,3,10,3) #高斯噪声
cv.imshow("add_noise",im)
add_gauss_noise(b,3,5,3)
cv.imshow("add_gauss_noise",b)
ima=ave_filter(im,3) #3位均值滤波
imb=ave_function(im,3) #3位系统均值滤波
imc=ave_filter(im,5) #5位均值滤波
imd=gauss_filter_self(im,5) #5位高斯滤波
ime=gauss_function(im,3) #3位系统高斯滤波
imf=mid_filter(im,3)
#3位中值滤波
img=mid_function(im,3) #3位系统中值滤波
imh=mid_filter(im,5) #5位中值滤波
cv.imshow("ave_self_3*3",ima)
cv.imshow("ave_function_3*3",imb)
cv.imshow("ave_self_5*5",imc)
cv.imshow("gauss_self_3*3",imd)
cv.imshow("gauss_function_3*3",ime)
cv.imshow("mid_self_3*3",imf)
cv.imshow("mid_function_3*3",img)
cv.imshow("mid_self_5*5",imh)
im1=sobel_filter_self(im)#Sobel算子
im2=sobel_function(im)#系统Sobel算子
im3=laplacian_filter_self(im)#laplace算子
im4=laplacian_function(im)#系统laplace算子
cv.imshow("sobel_filter_self",im1)
cv.imshow("sobel_function",im2)
cv.imshow("laplacian_filter_self",im3)
cv.imshow("laplacian_function",im4)
print("init:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(a,a),psnr(a,a),ssim(a,a)))
print("add_salt:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(im,a),psnr(im,a),ssim(im,a)))
print("a:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(ima,a),psnr(ima,a),ssim(ima,a)))
print("b:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(imb,a),psnr(imb,a),ssim(imb,a)))
print("c:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(imc,a),psnr(imc,a),ssim(imc,a)))
print("d:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(imd,a),psnr(imd,a),ssim(imd,a)))
print("e:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(ime,a),psnr(ime,a),ssim(ime,a)))
print("f:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(imf,a),psnr(imf,a),ssim(imf,a)))
print("g:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(img,a),psnr(img,a),ssim(img,a)))
print("h:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(imh,a),psnr(imh,a),ssim(imh,a)))
print("im1:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(im1,a),psnr(im1,a),ssim(im1,a)))
print("im2:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(im2,a),psnr(im2,a),ssim(im2,a)))
print("im3:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(im3,a),psnr(im3,a),ssim(im3,a)))
print("im4:MSE=%.2f PSNR=%.2f SSIM=%.2f"%(mse(im4,a),psnr(im4,a),ssim(im4,a)))
cv.waitKey(0)