详解APM的开方控制器sqrt_controller前言源码阅读数学原理MATLAB绘制曲线

前言

前面说过，sqrt_controller是对P项进行整定用途的，目的就是让P项的控制响应“软”下来，实际上就是一个经过改进的P控制器。读懂了sqrt_controller，那么你对APM的P控制器就了解得差不多了。

仅讨论P控制器，sqrt_controller的作用就是设定一个量linear_dist，以这个量的正负值为分界线划分出一个线性区域范围，在这个范围内表示误差量还很小，遵循Kp*error计算方式输出控制量。

超过linear_dist后，表明误差较大，此时不能由着误差单纯按照线性方式乘以Kp输出控制量，需要按照开方形式，使用另外的方式计算出实际控制量，此处后面补充。

在开始讲解源码之前，先来补充个前提：

了解飞控的应该都清楚，一般是使用串级PID来进行姿态等的控制。在APM中，外环角度环就是接收期望与实际的角度误差，然后输入到P控制器中得到期望的角速率。也就是说，这个控制过程可以表示为：
$$w=K_p\ast erro{r}_{\theta }$$

而我们同样知道，假定小角度内速率恒定，那么可知$w=erro{r}_{\theta }/dt$，而由此可直接定义
$$Kp=1/dt$$

而实际上APM中广泛采用了这个方式，因此，后续过程中我们谈论到Kp表明的都是时间的倒数。

源码阅读

数学公式的原理放在后面讲解，这边先放源码

// Proportional controller with piecewise sqrt sections to constrain second derivative
// 翻译：具有分段sqrt截面以约束二阶导数的比例控制器
// error：输入参数，误差量
// p：输入参数，Kp值
// second_ord_lim：输入参数，二阶限制，对Kp进行二次限制，通常是加速度最大值输入
// dt：输入参数，时间
float AC_AttitudeControl::sqrt_controller(float error, float p, float second_ord_lim, float dt)
{
    float correction_rate;	// 最后需要返回的期望速率
    if (is_negative(second_ord_lim) || is_zero(second_ord_lim)) {
        // 二阶限制是否为负或者零
		// 是的话表明开方控制器不起作用，按照正常方式计算Kp*error
        correction_rate = error * p;
    } else if (is_zero(p)) {
        // Kp=0但是我们开启了二阶限制则采用如下计算方式
        if (is_positive(error)) {
            correction_rate = safe_sqrt(2.0f * second_ord_lim * (error));
        } else if (is_negative(error)) {
            correction_rate = -safe_sqrt(2.0f * second_ord_lim * (-error));
        } else {
            correction_rate = 0.0f;
        }
    } else {
        // 如果同时定义了Kp和二阶限制
		// 一般我们用了sqrt_controller都是进的这个函数
		// 计算获取分界点linear_dist
		// 根据error与linear_dist的相对大小采用不同公式
        float linear_dist = second_ord_lim / sq(p);
        if (error > linear_dist) {
            correction_rate = safe_sqrt(2.0f * second_ord_lim * (error - (linear_dist / 2.0f)));
        } else if (error < -linear_dist) {
            correction_rate = -safe_sqrt(2.0f * second_ord_lim * (-error - (linear_dist / 2.0f)));
        } else {
            correction_rate = error * p;
        }
    }
    if (!is_zero(dt)) {
        // 这样可以确保在最后一个时间步过分校正错误不会使我们产生小的振荡。
        return constrain_float(correction_rate, -fabsf(error) / dt, fabsf(error) / dt);
    } else {
        return correction_rate;
    }
}

数学原理

初看这部分程序容易看的云里雾里的，没事，这边带大家重头开始梳理。

后续过程中，我们定义参数p为Kp，second_ord_lim为加速度最大值$a_{max}$；后面部分用error表明位移量的误差，v表示速度进行推导。

首先，我们来带大家回顾一下高中知识，还记得高中小车问题里面，位移、速度、加速度和时间中如果已知其中几个量怎么求另外几个吗，我这边直接给出：
$$x=v_{0}t+\frac{1}{2}a{t}^2$$$$2ax=v_t^2-v_0^2$$

那么回到我们的源程序中，我将直接从同时定义了Kp和二阶限制的else部分开始讲。

首先是这部分函数

float linear_dist = second_ord_lim / sq(p);

如前所述，$K_p=1/dt$，那么下面这段程序可以解释为如下（后面把$dt$简化表示为$t$）
$$linear\_dist=\frac{a_{max}}{K_p^2}=a_{max}{t}^2$$

那么由此也可以推算下面这行代码表示的公式

correction_rate = safe_sqrt(2.0f * second_ord_lim * (error - (linear_dist / 2.0f)));

$$correction\_rate=\sqrt{2a_{max}(error-(\frac{linear\_dist}{2}))}=\sqrt{2a_{max}(error-\frac{a_{max}{t}^2}{2}})$$

假定初始速度$v_0$为0，那么由 $2ax=v_t^2$ 和 $x=\frac{1}{2}a{t}^2$ 可进一步推算上面的公式
$$correction\_rate=\sqrt{2a_{max}(error-x^{\prime })}=\sqrt{2\ast a_{max}\ast △x}=v$$

如果$error$表示的是角度误差，角速度用$w$表示的话，那么同样的$correction\_rate$计算出来的即是期望的角速率，实际上姿态控制器中就是如此的计算。

那么如果没有定义Kp仅定义了二阶限制的这部分函数我想你肯定也已经能够看懂了，我就不多做解释了

correction_rate = safe_sqrt(2.0f * second_ord_lim * (error));

由此，sqrt_controller的内容想必大家应该就能完全理解了。

MATLAB绘制曲线

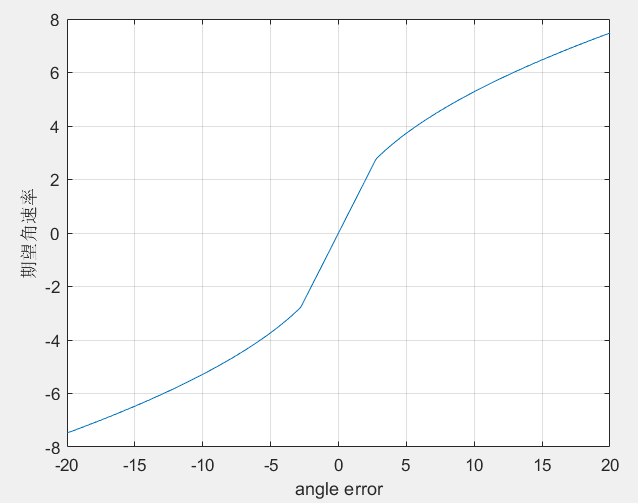
这边用MATLAB绘制了一下sqrt_controller的控制曲线。可以很明显看到在一段区域内是以线性方式进行递增，而当误差过大，达到一定值的时候，则是按照开方函数曲线进行递增。

函数给出如下（太久没用Matlab了，原谅我写的简陋）：

sqrt_controller函数：

function correction_rate = sqrt_controller(error,p,sencond_ord_lim,dt)

if sencond_ord_lim<0 || sencond_ord_lim==0
    rate = p.*error;
elseif p==0
    if error>0
        rate = sqrt(2.*sencond_ord_lim.*error);
    elseif error<0
        rate = -sqrt(2.*sencond_ord_lim.*(-error));
    else
        rate = 0;
    end
else
    linear_dist = sencond_ord_lim/(p.*p);
    if error>linear_dist
        rate = sqrt(2.*sencond_ord_lim.*(error-(linear_dist./2)));
    elseif error<-linear_dist
        rate = -sqrt(2.*sencond_ord_lim.*(-error-(linear_dist./2)));
    else
        rate = p.*error;
    end
end

if dt~=0
    if rate < -abs(error)/dt
        correction_rate = -abs(error)./dt;
    elseif rate > abs(error)/dt
        correction_rate = abs(error)./dt;
    else
        correction_rate = rate;
    end
else
    correction_rate = rate;
end

end

绘图程序：

Kp = 4.5;
sencond_ord_lim = 1.4;
dt = 1;
R = zeros(1,401);
i = 1;

for error = -20:0.1:20
    rate = sqrt_controller(error,Kp,sencond_ord_lim,dt);
    R(1,i)=rate;
    i = i+1;
end

plot(-20:0.1:20,R);
grid on
ylabel("期望角速率")
xlabel("angle error")

参考资料：
[算法] 刹车距离 get_stopping_point 和开方控制器 sqrt_controller
[飞控]姿态控制-开方控制器和倾斜角转加速度函数

最后

以上就是坚强方盒为你收集整理的详解APM的开方控制器sqrt_controller前言源码阅读数学原理MATLAB绘制曲线的全部内容，希望文章能够帮你解决详解APM的开方控制器sqrt_controller前言源码阅读数学原理MATLAB绘制曲线所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。