Java移动推荐算法提取特征值_特征提取算法（3）——SIFT特征提取算子

目录：

前言

1、高斯尺度空间GSS

2、高斯差分DOG

用DoG检测特征点

GSS尺度选择

3、图像金字塔建立

用前一个octave中的倒数第三幅图像生成下一octave中的第一幅图像

每层octave为什么生成s+3幅图像

4、高斯核性质在SIFT中的应用

5、除去不好的特征点

6、给特征点赋值一个128维方向参数

7、根据SIFT进行Match

8、补充

前言

SIFT算子是一种检测局部特征的算法，通过求一幅图中的特征点及其有关尺寸scale和方向orientation的描述子得到特征，进行图像特征点匹配，获得了良好效果。每个特征点的SIFT特征是128维向量，因此计算量巨大。

不变性：具有尺寸和旋转不变性，即改变旋转角度、图像亮度、拍摄视角，仍然能够得到好的检测效果。

改进型：PCA-SIFT，如名称所说“主成分SIFT特征”，主要提取了128维特征向量中的20个特征，大大减少了计算。

高斯尺度空间(GSS - Gauss Scale Space)

这是一个初始化操作，尺度空间理论目的是模拟图像数据的多尺度特征。唯一能产生尺度空间的核为高斯核函数(高斯卷积核是实现尺度变换的唯一线性核)，所以我们将图像的尺度空间表示成一个函数L(x,y,σ)，它是由一个变尺度的高斯函数G(x,y,σ)与图像I(x,y)卷积产生的。即：

其中 G(x,y,σ) 是尺度可变高斯函数 ：

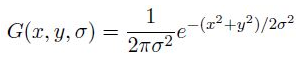
(x，y)是空间坐标，是尺度坐标。σ大小决定图像的平滑程度，大尺度对应图像的概貌特征，小尺度对应图像的细节特征。大的σ值对应粗糙尺度(低分辨率)，反之，对应精细尺度(高分辨率)。

高斯差分(DOG - Difference of Gauss)

为了有效的在尺度空间检测到稳定的关键点，提出了高斯差分尺度空间(DOG scale-space)。利用不同尺度的高斯差分核与图像卷积生成。

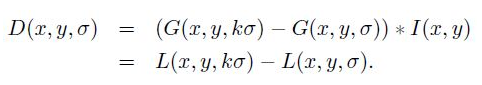
不同σ下图像尺度空间：

关于尺度空间的理解说明：2kσ中的2是必须的，尺度空间是连续的。在 Lowe的论文中 ，将第0层的初始尺度定为1.6(最模糊)，图片的初始尺度定为0.5(最清晰)。在检测极值点前对原始图像的高斯平滑以致图像丢失高频信息，所以 Lowe 建议在建立尺度空间前首先对原始图像长宽扩展一倍，以保留原始图像信息，增加特征点数量。尺度越大图像越模糊。

为什么用DoG来检测特征点？

Lindeberg证明用σ2标准化的高斯拉普拉斯(∇2G, LOG, Laplacian of Gauss)有着真正的尺度无关的特性，而Mikolajczyk发现，相比于其他一系列函数(比如梯度，Hessian，Harris角点函数等)，用σ2标准化的高斯拉普拉斯(σ2∇2G)有着更稳定的图像特征，因此σ2∇2G函数是我们理想的寻找特征点的函数。而在此，我们利用DoG来近似σ2∇2G。

通过热传导方程也可以帮助我们理解DoG与σ2∇2G之间的近似关系。由热传导方程可知(通常用t=σ2):

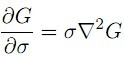
对上式进行有限差分运算得：

因此

DoG = G(x, y, kσ) − G(x, y, σ) ≈ (k − 1)σ2∇2G

而常数项(k - 1)并不会影响极值的位置。所以DoG是σ2∇2G的近似。

对于使用DoG来近似σ2∇2G，有如下优点：

σ2∇2G需要使用两个方向的高斯二阶微分卷积核，而DoG直接使用高斯卷积核，省去了对卷积核的生成的运算量。

DoG保留了各个高斯尺度空间的图像，这样，在生成某一空间尺度的特征时，可以直接尺度空间图像，而无需重新再次生成该尺度的图像。

GSS尺度选择

DoG近似于(k − 1)σ2∇2G，对于常数k，即为相邻高斯尺度空间的两幅图像的尺度倍数，Lowe在文中提到，The approximation error will go to zero as k goes to 1, but in practice we have found that the approximation has almost no impact on the stability of extrema detection or loca