由不完全数组构造非完全(任意)二叉树构造二叉树&4种遍历方法

构造二叉树&4种遍历方法

        目的：通过一个任意数组（可以包含Null，而且空的节点没必要全部用Null值填充）来构造一个任意形式的二叉树（可以是完全二叉树，也可以是非完全二叉树）。

        看网上好多教程由数组构造二叉树都是“完全二叉树”，即使可以产生非完全二叉树也必须将空节点全部用Null表示填入数组中（这样其实就跟完全二叉树等效了）。这里用Python2和Java两种语言实现了通过任意数组构造任意二叉树。

        这样便可以模仿leetcode平台在自己的IDE中进行关于二叉树题目的debug了。

        另外，实现四种遍历方式（前序、中序、后序遍历，以及层次遍历），以print构造的二叉树。

1. Python2实现

    # 创建二叉树。 从含有None的数组创建非完全二叉树 !!!
    # 将list换成队列queue，pop(0)更方便。
    def creatTree(self, nums):
        if not nums:
            return None
        root = TreeNode(nums[0])
        nums.remove(nums[0])
        lst = [root]
        while(lst and nums):
            tmp = lst[0]
            lst.remove(lst[0])
            if tmp:
                left = nums[0]
                tmp.left = TreeNode(left) if left else None
                nums.remove(nums[0])
                lst.append(tmp.left)
                try:
                    right = nums[0]
                    tmp.right = TreeNode(right) if right else None
                    nums.remove(nums[0])
                    lst.append(tmp.right)
                except:
                    pass
        return root

这里其实使用queue更方便，从尾部push头部pop。

下边Python的遍历只写两种，前序和层次。

    # 先序遍历
    def preorder(self, root):
        """递归实现先序遍历"""
        if root == None:
            return
        print(root.val),
        self.preorder(root.left)
        self.preorder(root.right)

    # 层次遍历
    def levelOrder(self, root):
        if not root:
            return None
        queue = list()
        # queue = []
        queue.append(root)
        while(queue):
            node = queue.pop(0)
            print node.val,
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

2. Java实现

package leetcode.easy;

import java.util.LinkedList;
import java.util.Queue;

class TreeNode {
     int val;
     TreeNode left;
     TreeNode right;
     TreeNode(int x) { val = x; }
}


public class CreatBinaryTree {
    // 递归法构建完全二叉树,不是完全二叉树的话叶构建不出来。
    public static TreeNode createCompleteBT(Integer[] arr, int i) // 初始时,传入的i==0
    {
        TreeNode root = null; // 定义根节点

        if (i >= arr.length) // i >= arr.length 时,表示已经到达了根节点
            return null;
        // System.out.println(arr[i]);
        if (arr[i] == null) {  // 是null的话直接return，否则下面TreeNode(arr[i])会error。
            return null;
        }

        root = new TreeNode(arr[i]); // 根节点
        root.left = createCompleteBT(arr, 2*i+1); // 递归建立左孩子结点
        root.right = createCompleteBT(arr, 2*i+2); // 递归建立右孩子结点

        return root;
    }

    // 创建二叉树，从含有None的数组创建非完全二叉树 !!!
    // 将list换成队列queue，pop(0)更方便。
    public static TreeNode creatAnyBiTreeByArr(Integer[] arr){
        Queue<Integer> queue_num = new LinkedList<Integer>();
        for(int i=0;i<arr.length;i++){
            queue_num.add(arr[i]);
            // ((LinkedList<Integer>) q1).add(null);
        }
        if (queue_num.isEmpty()) return null;
        TreeNode root = new TreeNode(queue_num.poll());  // poll() 方法在用空集合调用时不是抛出异常，只是返回 null !!
        Queue<TreeNode> que_node = new LinkedList<TreeNode>();
        que_node.offer(root);

        while (!que_node.isEmpty() && !queue_num.isEmpty()){
            TreeNode tmp = que_node.poll();
            if(tmp != null){
                Integer left = queue_num.poll();
                Integer right = queue_num.poll();
                if(left != null)
                    tmp.left = new TreeNode(left);
                else tmp.left = null;
                que_node.offer(tmp.left);

                if(right != null)
                    tmp.right = new TreeNode(right);
                else tmp.right = null;
                que_node.offer(tmp.right);
            }
        }
        return root;
    }

    // 先序遍历
    public static void preOrder(TreeNode root)
    {
        if (root == null)
            return;
        System.out.print(root.val+" ");
        preOrder(root.left);
        preOrder(root.right);
    }

    // 中序遍历
    public static void inOrder(TreeNode root)
    {
        if (root == null)
            return;
        inOrder(root.left);
        System.out.print(root.val+" ");
        inOrder(root.right);
    }

    // 后序遍历
    public static void postOrder(TreeNode root)
    {
        if (root == null)
            return;
        postOrder(root.left);
        postOrder(root.right);
        System.out.print(root.val+" ");
    }

    // 层次遍历
    public static void levelOrder(TreeNode root)
    {
        if (root == null){
            return;
        }
        //add()和remove()方法在失败的时候会抛出异常(不推荐)
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while (! queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.print(node.val+" ");
            if (node.left != null){
                queue.offer(node.left);
            }
            if (node.right != null){
                queue.offer(node.right);
            }
        }
    }

    // ########## test ##########
    public static void main(String[] args) {
        CreatBinaryTree sl = new CreatBinaryTree();

        //  ***************  ...
        Integer[] data1 = new Integer[] {0,1,2,null,3,4,null,5};
        Integer[] data3 = new Integer[] {0,1,null,2,null,3};
        TreeNode root1 = createCompleteBT(data1,0);
        TreeNode root2 = creatAnyBiTreeByArr(data1);

        // 构建任意二叉树
        TreeNode root3 = sl.creatAnyBiTreeByArr(data3);

        levelOrder(root1);  // 0 1 2 3 4
        System.out.println();

        preOrder(root1);  // 0 1 3 2 4
        System.out.println();
        preOrder(root2); // 0 1 3 5 2 4 
        System.out.println();

        sl.levelOrder(root3);  // 0 1 2 3
        System.out.println();
        sl.preOrder(root3);  // 0 1 2 3
    }
}

对比root1和root2的结果，同样的数组，不同的树结构，因为前者只能构造“完全二叉树”或者由Null值填充空位的伪完全二叉树（如将data1填充成为[0,1,2,null,3,4,null,null,null,5], 便可以通过createCompleteBT 函数构造与后者creatAnyBiTreeByArr相同的形式了）。

3. 树结构可视化

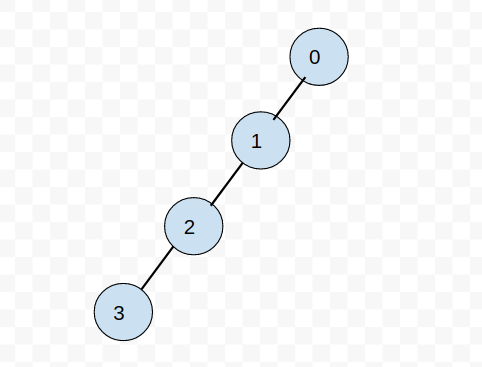
如数组[0, 1, null, 2, null, 3] 通过creatAnyBiTreeByArr函数构造出来的数的形式如下图，这里不需要把此数组填充成为[0, 1, null, 2, null, null, null, 3].

最后

以上就是温柔小蝴蝶为你收集整理的由不完全数组构造非完全(任意)二叉树构造二叉树&4种遍历方法的全部内容，希望文章能够帮你解决由不完全数组构造非完全(任意)二叉树构造二叉树&4种遍历方法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。