各种各样的二叉树你还记得它们都是什么吗？ 简单介绍基本的6种二叉树及操作（一）

二叉树的基本概念

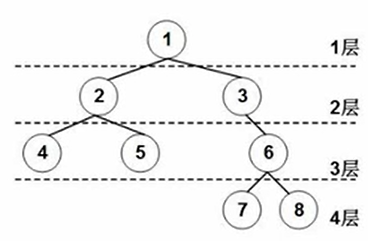
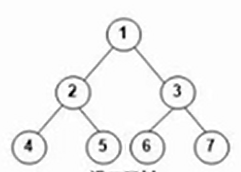
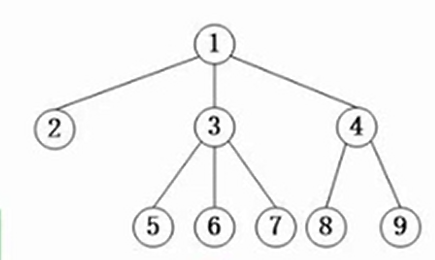
（图1-1 二叉树）
结点的度：指一个结点的拥有多少个孩子结点
如1号结点有俩个孩子，所以1号结点的度为2。而7号结点无孩子，所以7号结点的度为0。
树的度 ：所有结点中最高的度数就是结点的度。
叶子结点：无孩子结点的结点。
分支结点：除了叶子结点的结点（即有孩子的结点）
内部结点：除了叶子结点和根结点的结点
父结点：（相对概念）子结点的父亲结点
子结点：（相对概念）父结点的儿子结点
兄弟结点：一般指同一父结点下的不同儿子结点（特殊情况：（堂兄弟）也有指父亲的父亲的儿子的儿子结点）
层次：层次数等于离根结点的距离

满二叉树与完全二叉树

满二叉树：除最后一层，其他层结点都有左右儿子
完全二叉树：除了最后一层，上面的是满二叉树（并且结点的编号连续）（满二叉树一定是完全二叉树）
非完全二叉树：不是完全二叉树的树。
如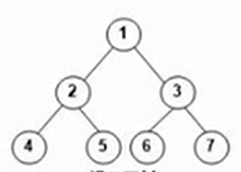
（图1-2满二叉树）

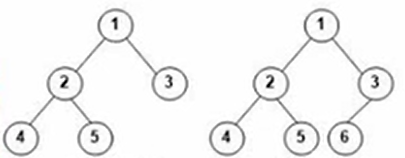
（图1-3完全二叉树）

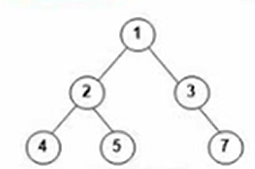
（图1-4 非完全二叉树）

图1-4中，没有6号结点所以不是完全二叉树

二叉树的特性

1. 第i层最多有2的 i-1 次方个结点（满二叉树时）
2. 深度为 k 的二叉树，最多有 2的k次方 - 1的结点 （从第一层到第k层的结点树相加，就是2的k次方 - 1）
3. 如果叶子结点的数量为n，度为2的结点数为m。那么！ n = m + 1 （对任意二叉树适用）
4. 对于有 n 个结点的完全二叉树编号为 1 层 到 （log 2 n）+ 1层。则对于任一结点的编号为 i 。它的左儿子编号为2 * i ，它的右儿子编号为2 * i + 1。[ i / 2 ] 为父结点 ( [] 向下取整）
   

二叉树的遍历

分为前序遍历、中序遍历和后序遍历。

• 前序遍历：先访问根结点，然后左儿子，再右儿子
• 中序遍历：先访问左儿子，然后访问根结点，再访问右儿子
• 后序遍历：先访问左儿子，然后访问右儿子，再访问根结点
• 就是说，前中后的概念是针对于根结点遍历的次序。

反向构造二叉树

如果知道前序和中序，怎么样构造一棵二叉树

比如
前序：ABHFDECG
中序：HBEDFAGC

根据前序中序的性质，可以知道——前序找根（父结点），中序分左右儿子

（1）
前序：ABHFDECG
中序：HBEDFAGC

由前序知：
根为A

把A代入中序得

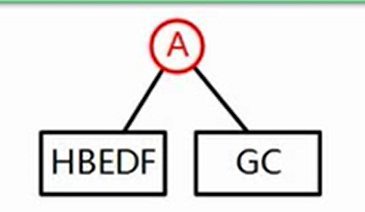
HBEDF A GC

HBEDF为A的左子树
GC为A的右子树

（2）
前序：A | {B} H FDE | CG
中序：H {B} EDF |A| GC

然后再看前序 ：A后面是B
可得
左子树中
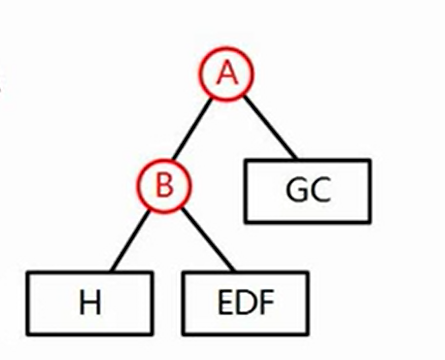
H B EDF

H是B的左子树
EDF是B的右子树

（3）
前序：A | {B} H FDE | CG
中序：H {B} EDF |A| GC
再看前序：知道FDE中 F在前面，F为父结点

在中序中F，ED在 F 的左边

在前序中，D在E的前面 D为E的父亲
在中序中，E在D前面 E是D的左儿子

得到：

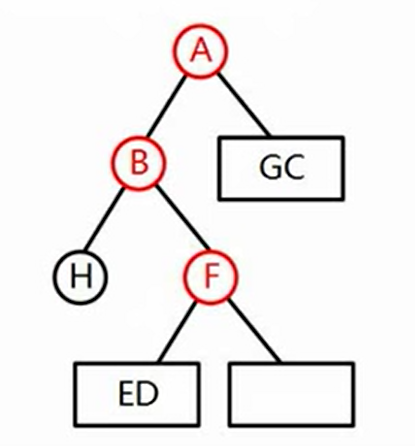
同理可以构造A的右子树

树转二叉树

把一个普通的树转换为二叉树的思想就是：

• 孩子结点 ——> 左子树
• 兄弟结点 ——> 右子树
• 并且在所有孩子结点中，最左边的是左子树的根结点。
• 并且在所有兄弟结点中，最左边的是右子树的根结点。
  
  根据这个思想有俩种方法把树转成二叉树：

一、直接构造

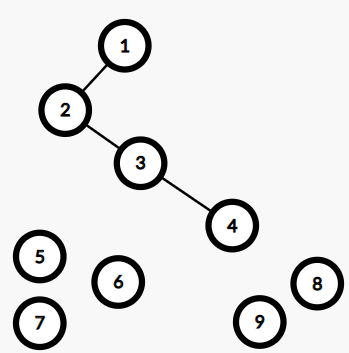
对（1）来说，2、3、4是它的儿子结点。把他们作为（1）的左子树，且2是左子树的根结点。

对于（2）来说，3、4是它的兄弟结点，作为（2）的右子树，并且3是右子树的根结点。

同理，
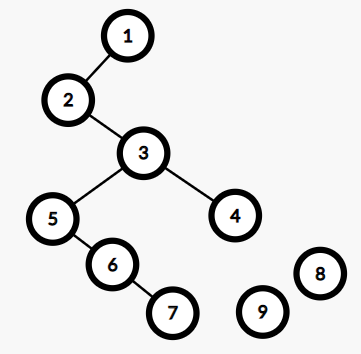
对于（3）来说，5、6、7是他的儿子结点，把他们作为（3）的左子树，且5是左子树的根结点。

对于（5）来说，6、7是他的兄弟结点，把他们作为（5）的右子树，且6是右子树的根结点。

对于6来说，7是他的兄弟结点，所以7是它的右儿子。

同理，
对于（4）结点。8、9是它的儿子结点，作为左子树。
且8是左子树的根结点。

对于（8）来说，9是8的兄弟结点，所以9是8的右儿子。

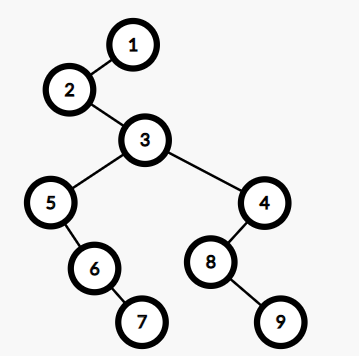
这样，就完成了数转二叉树。

二、连线法（快得多）

还可以直接通过连线法来构造。

连续的要点是：

• 父结点连最左边的儿子结点
• 最左边的儿子结点连所有的兄弟结点
• 然后把其他线都砍掉。
• 剩下的稍稍移动一个角度（把连接兄弟结点的线顺时针移）就构成了二叉树。

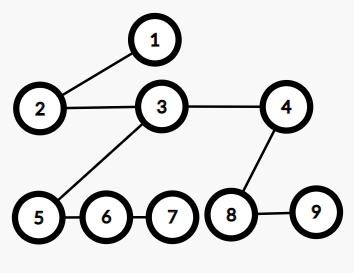
连接兄弟的线顺时钟移动
连接儿子的线保持这个角度

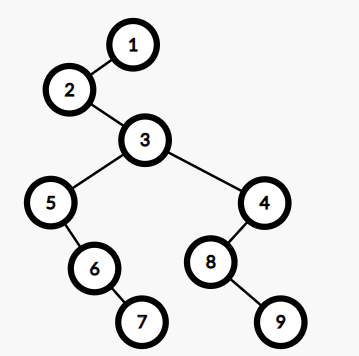
这样同样构造完成。

最后

以上就是眼睛大乌龟为你收集整理的各种各样的二叉树你还记得它们都是什么吗？ 简单介绍基本的6种二叉树及操作（一）的全部内容，希望文章能够帮你解决各种各样的二叉树你还记得它们都是什么吗？ 简单介绍基本的6种二叉树及操作（一）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。