二叉树的遍历及相关算法

概念

二叉树是每个节点最多拥有两个子树的树结构，它的子树（左子树、右子树）也是二叉树

一、前中后序遍历

前序 首先访问根节点、然后遍历左子树、然后遍历右子树
中序 首先遍历左子树、然后访问根节点、然后遍历右子树
后序 首先遍历左子树、然后遍历右子树、然后访问根节点

public boolean isSymmetric(TreeNode node) {
  if (node==null){
      return true;
  }
  Queue<TreeNode> queue = new LinkedList<>();
  queue.add(node.left);
  queue.add(node.right);
  while (!queue.isEmpty()){
      //每次需要比较两个节点
      TreeNode left = queue.poll();
      TreeNode right = queue.poll();
      if (left==null && right==null){
          return true;
      }
      if (right==null || left==null){
          return false;
      }
      if (left.val!=right.val){
          return false;
      }
      //注意入队顺序，此时当前节点左右节点都存在
      queue.add(left.left);
      queue.add(right.right);
      queue.add(left.right);
      queue.add(right.left);
  }
  return true;
 }

使用递归求解遍历

正常给一棵树，递归的写法基本一致，只是遍历的顺序不同、获取节点值的顺序不同而已，如下一棵树treeSofia：
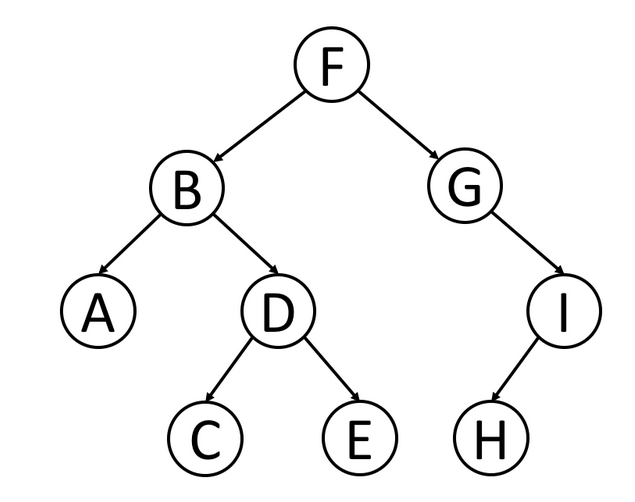不考虑顺序，递归写法应该是：

/**
 * @className binaryTree
 * @Author sofia
 * @Date 2022/1/16
 * @Describe
 **/
public class binaryTree {
    public static class Node{
        public int value;
        public Node left;
        public Node right;
    }
    
    //递归得到递归序
    public static void func(Node head){
        if (head==null) return;
        //
        func(head.left); 
        //
        func(head.right);
        //
    }
}

按照func的方法得到treeSofia的递归序为：
FBAAABDCCCDEEEDBFGGIHHHIIGF

• 注意在递归序中，每个节点都出现了三次，这是因为在递归的最开始部分做了判空操作，若节点为空则返回，比如叶子节点A，第一次访问是通过节点B的左子节点，第二次是递归访问A的左子节点，发现A.left = null于是返回到A本身，第三次是递归访问A的右子节点，发现A.right = null于是返回到A，其他节点同理都有三次访问。
• 知道了二叉树的递归序后再获取前中后序就容易了，事实上前序就是递归序中每个节点第一次出现的时候，为

FBAAABDCCCDEEEDBFGGIHHHIIGF
FBADCEGIH

中序就是递归序中每个节点第二次出现的时候，为

FBAAABDCCCDEEEDBFGGIHHHIIGF
ABCDEFGHI

后序就是递归序中每个节点第三次出现的时候，为

FBAAABDCCCDEEEDBFGGIHHHIIGF
-> ACEDBHIGF

若题目要求将结果放入到一个list中返回，那么前中后序写法就应该是：
前序：

List<Integer> list = new ArrayList<>();
public void funcPreOrder(Node head){
     if (head==null) return;
     list.add(head.value);
     funcPreOrder(head.left);
     funcPreOrder(head.right);
 }

中序：

 List<Integer> list = new ArrayList<>();
 public void funcInOrder(Node head){
      if (head==null) return;
      funcInOrder(head.left);
      list.add(head.value);
      funcInOrder(head.right);
  }

后序：

 List<Integer> list = new ArrayList<>();
 public void funcPostOrder(Node head){
     if (head==null) return;
     funcPostOrder(head.left);
     funcPostOrder(head.right);
     list.add(head.value);
 }

使用迭代求解遍历

迭代求先序需要借助栈，具体的思路为（入栈顺序中、右、左）：

1. 从栈里弹出一个节点
2. 处理节点（打印或者放入list等）
3. 先右后左将节点放入栈中
4. 重复1-3

public List<Integer> preOrderByIteration(Node head){
    List<Integer> resultList = new ArrayList<>();
     Stack<Node> stack = new Stack<>();
     if (head==null) return resultList;
     stack.add(head);
     while (!stack.isEmpty()){
         head = stack.pop();
         resultList.add(head.value);
         if (head.right!=null){
             stack.add(head.right);
         }
         if (head.left!=null){
             stack.add(head.left);
         }
     }
     return resultList;
 }

迭代求中序需要借助栈，具体的思路为：

1. 先将树的左节点全部入栈
2. 弹出左节点并处理
3. 对弹出节点的右子树做1、2操作

public static List<Integer> inOrderByIteration(Node head){
    List<Integer> resultList = new ArrayList<>();
     if (head==null) return resultList;
     Stack<Node> stack = new Stack<>();
     while (head!=null || !stack.isEmpty()){
         if (head!=null){
             stack.push(head.left);
             head = head.left;
         }else {
             head = stack.pop();
             resultList.add(head.value);
             head = head.right;
         }
     }
     return resultList;
 }

迭代求后序可以通过借助2个栈，具体的思路为：

• 根节点入stack1后弹出到stack2
• 先左后右进stack1
• 重复1、2

public static List<Integer> postorderByIteration(Node head){
        List<Integer> resultList = new ArrayList<>();
        Stack<Node> stack1 = new Stack<>();
        Stack<Node> stack2 = new Stack<>();
        if (head==null) return resultList;
        stack1.push(head);
        while (!stack1.isEmpty()){
            head = stack1.pop();
            stack2.push(head);
            if (head.left!=null){
                head = head.left;
                stack1.push(head.left);
            }
            if (head.right!=null){
                head = head.right;
                stack1.push(head);
            }
        }
        while (!stack2.isEmpty()){
            resultList.add(stack2.pop().value);
        }
        return resultList;
    }

后序迭代还有一种方式就是使用一个栈一个list，将出栈的元素依次放入到list中，使用list.reverse()方式即为所求。

二、层序遍历

层序遍历需要借助队列，基本思路：

1. 根节点入队列
2. 队列不为空则出队列并操作节点
3. 若左节点存在则入队列、右结点存在则入队列
4. 重复2、3

 public List<Integer> levelOrder(Node root) {
    List<Integer> list = new ArrayList();
    if(root==null) return list;
    //双向链表的本质是queue
    Queue<Node> queue = new LinkedList<>();
    if(root==null) return list;
    queue.add(root);
    while(!queue.isEmpty()){
        list.add(queue.poll().value);
        if(root.left!=null) queue.add(root.left);
        if(root.right!=null) queue.add(root.right);
    }
    return list;
}

三、求二叉树的最大宽度

• 求宽度需要用到队列
• 需要在遍历的时候记录当前层、当前层的节点数

//求二叉树的最大宽度
public static int getMaxWidth(TreeNode root){
    //定义变量用来存放当前层数，以及当前层节点数
    int curLevel = 1;
    int curLevelNodes = 0;
    //存放当前节点以及其所在的层数
    Map<TreeNode, Integer> tmpMap = new HashMap<>();
    int max = 0;
    tmpMap.put(root, curLevel);
    if(root==null) return max;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()){
        TreeNode currRoot = queue.poll();
        int level = tmpMap.get(currRoot);
        if (level==curLevel){
            curLevelNodes++;
            //注意max在进入下一层之前更新
            max = Math.max(max,curLevelNodes);
        }else {
            curLevelNodes=1;
            curLevel++;
        }
        if (currRoot.left!=null){
            tmpMap.put(currRoot.left, curLevel+1);
            queue.add(currRoot.left);
        }
        if (currRoot.right!=null){
            tmpMap.put(currRoot.right,curLevel+1);
            queue.add(currRoot.right);
        }
    }
    return max;
}

四、求二叉树的最大深度

掌握求宽度后求深度就很简单了，只是去掉记录每层节点数的过程

//求二叉树的最大深度
public static int getMaxDepth(TreeNode node){
    int max = 0;
    int curLevel = 1;
    Map<TreeNode, Integer> depthMap = new HashMap<>();
    if (node==null) return max;
    max = curLevel;//如果根节点存在，则max由0变为1
    Queue<TreeNode> queue = new LinkedList<>();
    depthMap.put(node,curLevel);
    queue.add(node);
    while (!queue.isEmpty()){
        TreeNode curNode = queue.poll();
        Integer level = depthMap.get(curNode);
        //不在同一层，深度加1
        if (level!=curLevel){
            max = Math.max(max, level);
            curLevel++;
        }
        if (curNode.left!=null){
            queue.add(curNode.left);
            depthMap.put(curNode.left, curLevel+1);
        }
        if (curNode.right!=null){
            queue.add(curNode.right);
            depthMap.put(curNode.right, curLevel+1);
        }
    }
    return max;
}

使用递归就更简单了

public int maxDepth(TreeNode root) {
   return root==null? 0 : Math.max(maxDepth(root.left), maxDepth(root.right))+1;
}

五、判断一颗二叉树是否对称

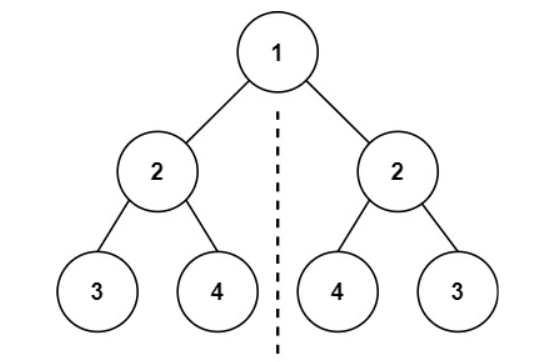
1 如果某个节点的左右节点都存在，则

• 左节点的左节点==右节点的右节点
• 左节点的右节点==右节点的左节点

2 左节点存在右节点不存在false,右节点存在左节点不存在false,左右节点都不存在true
3 需要借助队列

 //判断一颗二叉树是否对称
public static Boolean isSymmetric(TreeNode node){
    if (node==null){
        return true;
    }
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(node.left);
    queue.add(node.right);
    while (!queue.isEmpty()){
        //每次需要比较两个节点
        TreeNode left = queue.poll();
        TreeNode right = queue.poll();
        if (left==null && right==null){
            continue;
        }
        if (right!=null && left==null){
            return false;
        }
        if (right==null && left!=null){
            return false;
        }
        if (right.val!=left.val){
            return false;
        }
        //注意入队顺序，此时当前节点左右节点都存在
        queue.add(left.left);
        queue.add(right.right);
        queue.add(left.right);
        queue.add(right.left);
    }
    return true;
}

递归写法，简单点

 public boolean isMirror(TreeNode root1, TreeNode root2){
        if (root1==null && root2==null) return true;
        if (root1!=null^root2!=null) return false;
        return (root1.val==root2.val)&&isMirror(root1.left,root2.right)&&isMirror(root1.right,root2.  left);
    }
    public boolean isSymmetric(TreeNode node){
        return isMirror(node.left,node.right);
    }

六、路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false

递归写法

public boolean hasPathSum(TreeNode root, int targetSum) {
	if (root==null) return false;
	   if (root.left==null&&root.right==null){
	       return targetSum==root.val;
	   }
	return hasPathSum(root.left,targetSum-root.val)||hasPathSum(root.right, targetSum-root.val);
}

非递归写法

//路径总和之非递归写法
public static boolean hasPathSum2(TreeNode root, int targetSum){
    if (root==null) return false;
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()){
        TreeNode curNode = stack.pop();
        //true的条件是：存在叶子节点的值累加后与目标和相等
        if (curNode.left==null&&curNode.right==null){
            if (targetSum-curNode.val==0){
                return true;
            }
        }
        if (curNode.left!=null){
            curNode.left.val = curNode.left.val+curNode.val;
            stack.push(curNode.left);
        }
        if (curNode.right!=null){
            curNode.right.val = curNode.right.val+curNode.val;
            stack.push(curNode.right);
        }
    }
    return false;
}

最后

以上就是糊涂煎蛋为你收集整理的二叉树的遍历及相关算法的全部内容，希望文章能够帮你解决二叉树的遍历及相关算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。