二叉树的遍历（递归与队列）

遍历
就是按照某种次序访问树中的所有结点，且每个结点恰好访问一次。
也就是说，按照访问的次序，可以得到由树中所有结点排成一个序列。
树的遍历也可以看成人为的将非线性结构线性化。

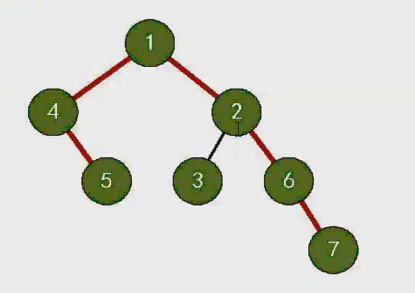
将整个二 叉树看做三部分：根、左子树、右子树、、如果规定先遍历左子树、再遍历右子树。那么根据根的遍历顺序就有三种遍历方式。

先序/根遍历DLR: 根 左子树 右子树
中序/根遍历LDR: 左子树 根 右子树
中序/根遍历LRD: 左子树 右子树 根

注意：由于树的递归定义，其实对三种遍历的概念其实也是一个递归的描述过程

先序遍历：1，4，5，2，3，6，7
中序遍历：4，5，1，3，2，6，7
后序遍历：5，4，3，7，6，2，1

分析流程：

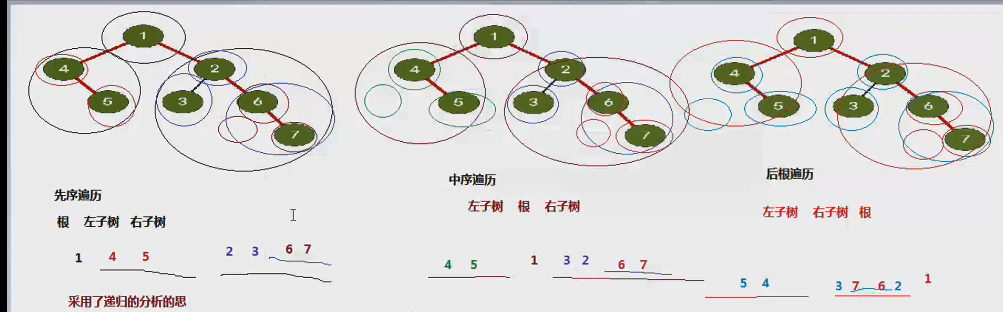
递归实现遍历二叉树
先建立一个结点对象

public class Node {
	Object Value;	//结点值
	Node leftChild; //左子树的引用
	Node rightChild;//右子树的引用
	public Node(Object value, Node leftChild, Node rightChild) {
		super();
		Value = value;
		this.leftChild = leftChild;
		this.rightChild = rightChild;
	}
	public Node(Object value) {
		super();
		Value = value;
	}
	
}

实现遍历

public class BinaryTree {

	private Node node;

	public BinaryTree(Node node) {
		super();
		this.node = node;
	}

	public BinaryTree() {
		super();
	}
	//判断是否为空
	public boolean isEmpty(){
		if (node !=null) {
			return true;
		}
		return false;
	}
	//先序遍历递归
	public void preOrder(){
		if (node !=null) {
			//打印根结点
			System.out.print(node.Value+"   ");
			//对左子树进行先序遍历
			//构建一个二叉树，根是左子树的根
			BinaryTree leftTree = new BinaryTree(node.leftChild);
			leftTree.preOrder();
			//对右子树进行先序遍历
			//构建一个二叉树，根是左子树的根
			BinaryTree rightTree = new BinaryTree(node.rightChild);
			rightTree.preOrder();
		
		}

	}
	//中序遍历
	public void inOrderTraverse(){
		System.out.println("中序遍历");
		this.inOrderTraverse(node);
		System.out.println("");
		
		
	}
	//中序遍历
	private void inOrderTraverse(Node node){
		if (node !=null) {
		//构建一个二叉树，根是左子树的根
		this.inOrderTraverse(node.leftChild);
		//打印根结点的值 
		System.out.print(node.Value+"   ");
		//构建一个二叉树，根是左子树的根
		this.inOrderTraverse(node.rightChild);
		}
	}
	//后序遍历
	public void postOrderTraverse(){
		System.out.println("后序遍历");
		this.postOrderTraverse(node);
		System.out.println("");
	}
	//后序遍历
	private void postOrderTraverse(Node node){
		if(node !=null){
			//遍历左子树
			this.postOrderTraverse(node.leftChild);
			//遍历右子树
			this.postOrderTraverse(node.rightChild);
			System.out.print(node.Value+"   ");
			
		}
	}
	//高度
	public int getHeight() {
		System.out.println("二叉树的高度是：");
		return this.getHeight(node);
	}
	private int getHeight(Node node) {
		if(node == null){
			return 0;
		}else {
			//获取左子树的高度
			int nl = this.getHeight(node.leftChild);
			//获取右子树的高度
			int nr = this.getHeight(node.rightChild);
			//返回左子树、右子树较大的高度并加1
			return nl > nr ? nl+1:nr+1;	
		}
	}
	
	
	
	//结点数
	public int size() {
		System.out.println("二叉数结点的个数：");
		return this.size(node);
	}
	private int size(Node node) {
		if (node == null) {
			return 0;
		}else {
			//获取左子树的结点数
			int nl = this.size(node.leftChild);
			//获取右子树的结点数
			int nr = this.size(node.rightChild);
			//返回左右子树的和加1；
			return nl+nr+1;
		}
	}
}

测试

public class Test {
	
	public static void main(String[] args) {
		//创建树
		Node node5 = new Node(5, null, null);
		Node node4 = new Node(4, null, node5);
		
		Node node3 = new Node(3, null, null);
		Node node7 = new Node(7, null, null);
		Node node6 = new Node(6, null, node7);
		Node node2 = new Node(2,node3, node6);
		
		Node node1 = new Node(1,node4, node2);
		
		BinaryTree btree = new BinaryTree(node1);
		
		//判断二叉树是否为空
		System.out.println(btree.isEmpty());
		
		//先序遍历递归
		System.out.println("先序遍历");
		btree.preOrder();
		System.out.println("");
		
		//中序遍历递归
		btree.inOrderTraverse();
		
		//后序遍历递归
		btree.postOrderTraverse();
		
		//二叉树的高度
		int h  = btree.getHeight();
		System.out.println(h);
		
		//二叉树的结点数量
		int n = btree.size();
		System.out.println(n);
		
		
	}
}

运行结果：

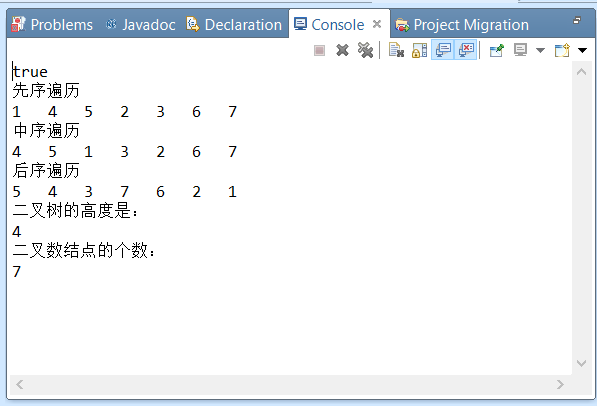
对一个二叉树的层次遍历，不能用递归的方法，借助队列来实现。
原理：先把根放进队列里面，然后在出栈，在根释放之前，把根的两个孩子都放到队列里面，并且是自左向右放的，相当于把一层结点处理完了，把第二层的结点也放进队列里面，然后在处理的第二层结点，在释放之前把第三层的结点自左向在放在结点里面，然后在处理第三层的结点，在处理第在层的结点的过程中把第四层的结点放进队列里面，因为队列是先进先出，所以要先放左边的，再放右边的；当所有的结点为空的时候结束 。

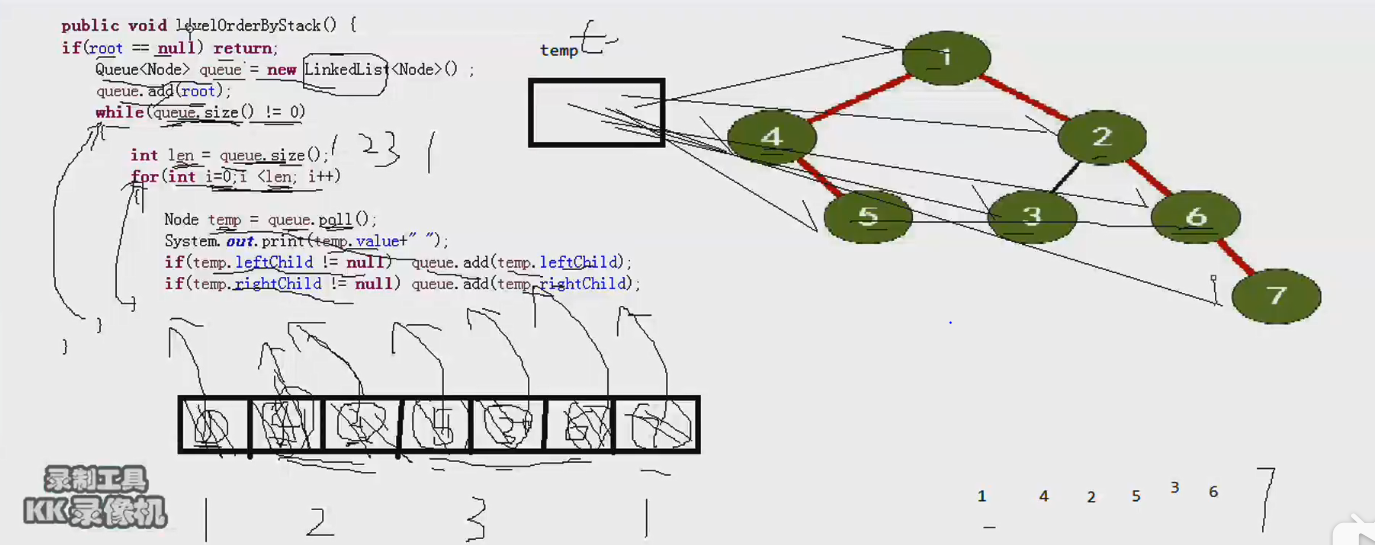
中序非递归遍历

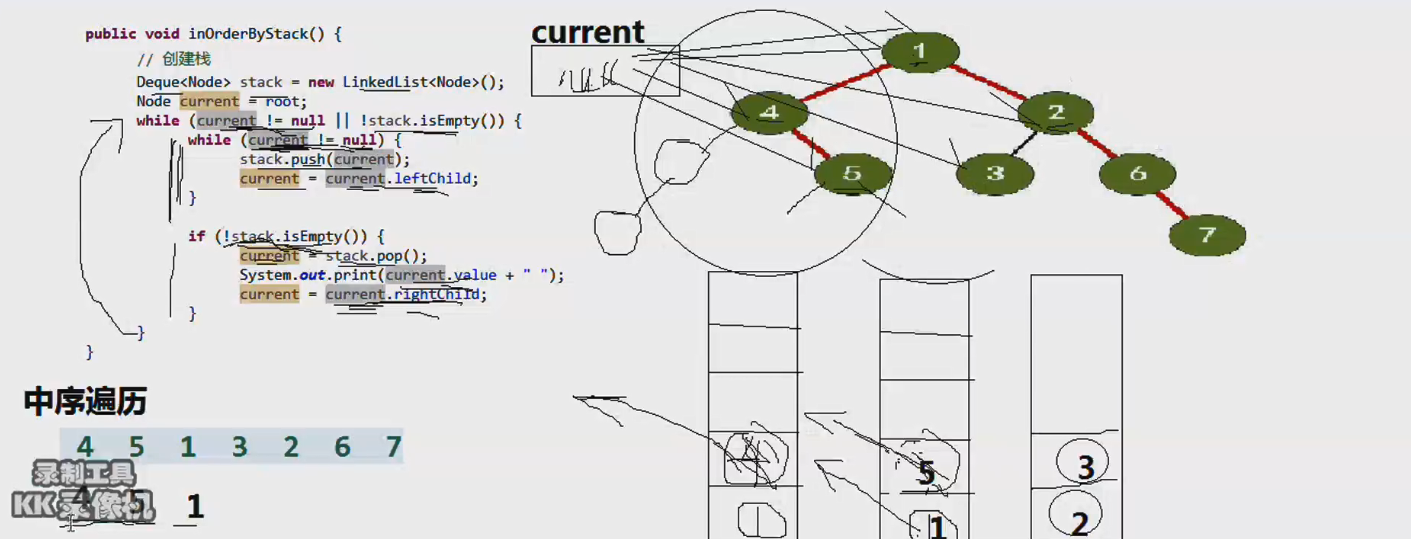
最后

以上就是欣慰果汁为你收集整理的二叉树的遍历（递归与队列）的全部内容，希望文章能够帮你解决二叉树的遍历（递归与队列）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。