二叉树的三种遍历（递归算法）C++1、先序遍历(NLR):过程：①先遍历根结点②遍历左子树③遍历右子树。得到的结果序列是：ABDGHECF2、中序遍历(LNR)：①先左子树②访问根结点③访问右子树。得到的结果序列是：GDHBEACF3、后序遍历(RLN)：①先左子树②访问右子树③访问根结点。得到的结果序列是：GHDEBFCA 总结：函数递归时，每次都是一个新的二叉树，执行完后，退出最内层、最内层-1层、最内层-2层....直到第一个根结点。

77 阅读 0 评论 51 点赞

我是靠谱客的博主高贵飞鸟，最近开发中收集的这篇文章主要介绍二叉树的三种遍历（递归算法）C++1、先序遍历(NLR):过程：①先遍历根结点②遍历左子树③遍历右子树。得到的结果序列是：ABDGHECF2、中序遍历(LNR)：①先左子树②访问根结点③访问右子树。得到的结果序列是：GDHBEACF3、后序遍历(RLN)：①先左子树②访问右子树③访问根结点。得到的结果序列是：GHDEBFCA 总结：函数递归时，每次都是一个新的二叉树，执行完后，退出最内层、最内层-1层、最内层-2层....直到第一个根结点。，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

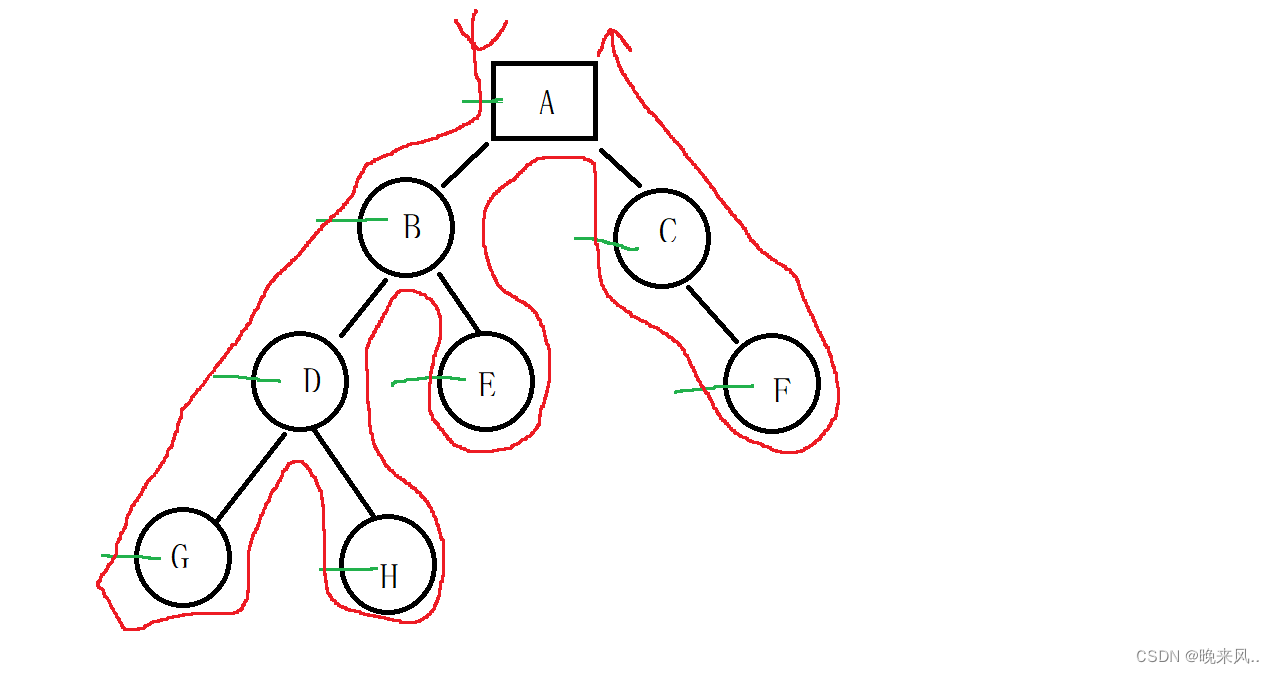
1、先序遍历(NLR):过程：①先遍历根结点②遍历左子树③遍历右子树。得到的结果序列是：ABDGHECF

算法如下：其中每一次递归都代表对一个新的二叉树进行运算，最先输出的是根结点，然后是根的左结点，又将左节点看成一个新的根结点再进行递归。

void PreOrder(BTree & bt)
{
   PreOrder(bt.r);
}

void PreOrder1(BTree * b)
{
   if(b!=NULL)
      {
        cout<<b->data; //访问根结点
        PreOrder1(b->lchild);  //访问左子树
        PreOrder1(b->rchild); //访问右子树
      }    
}

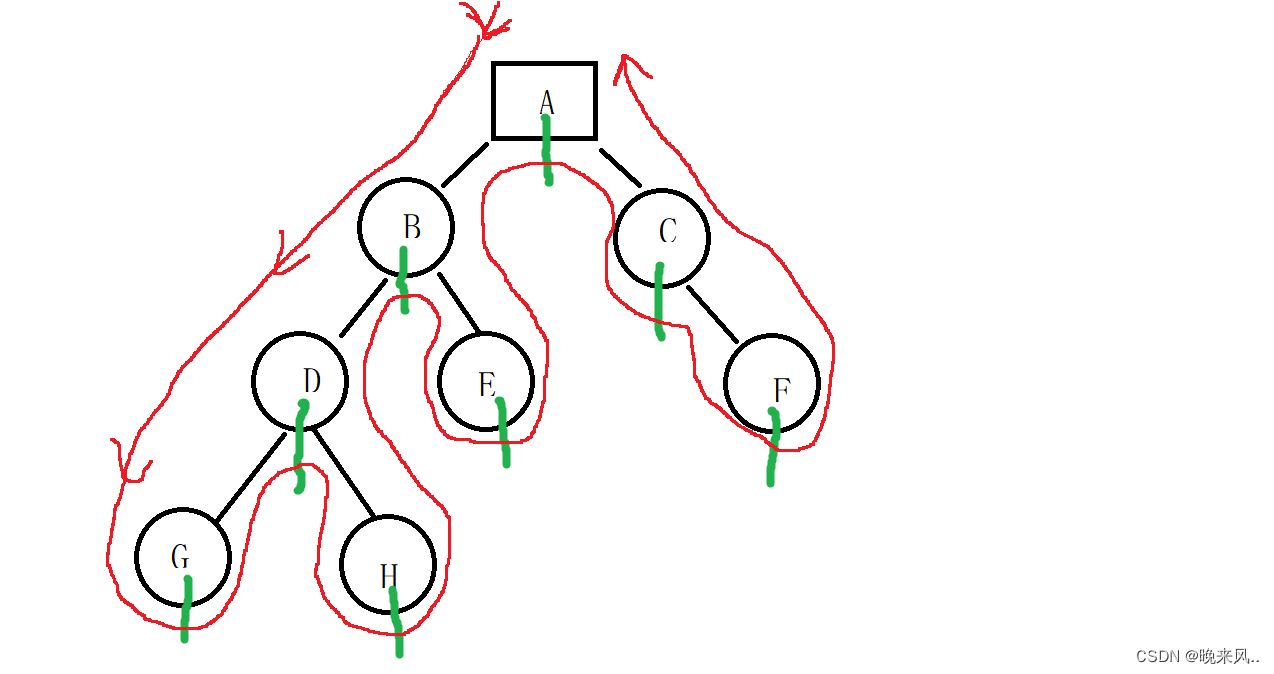
2、中序遍历(LNR)：①先左子树②访问根结点③访问右子树。得到的结果序列是：GDHBEACF

算法如下：中序遍历的核心是先输出以根为最后递归的地址为根输出其左子树，然后是根，然后是右子树

void InOrder(BTree & bt)
{
   InOrder(bt.r);
}

void InOrder1(BTree * b)
{
   if(b!=NULL)
      {
        InOrder1(b->lchild);  //访问左子树
        cout<<b->data; //访问根结点
        InOrder1(b->rchild); //访问右子树
      }    
}

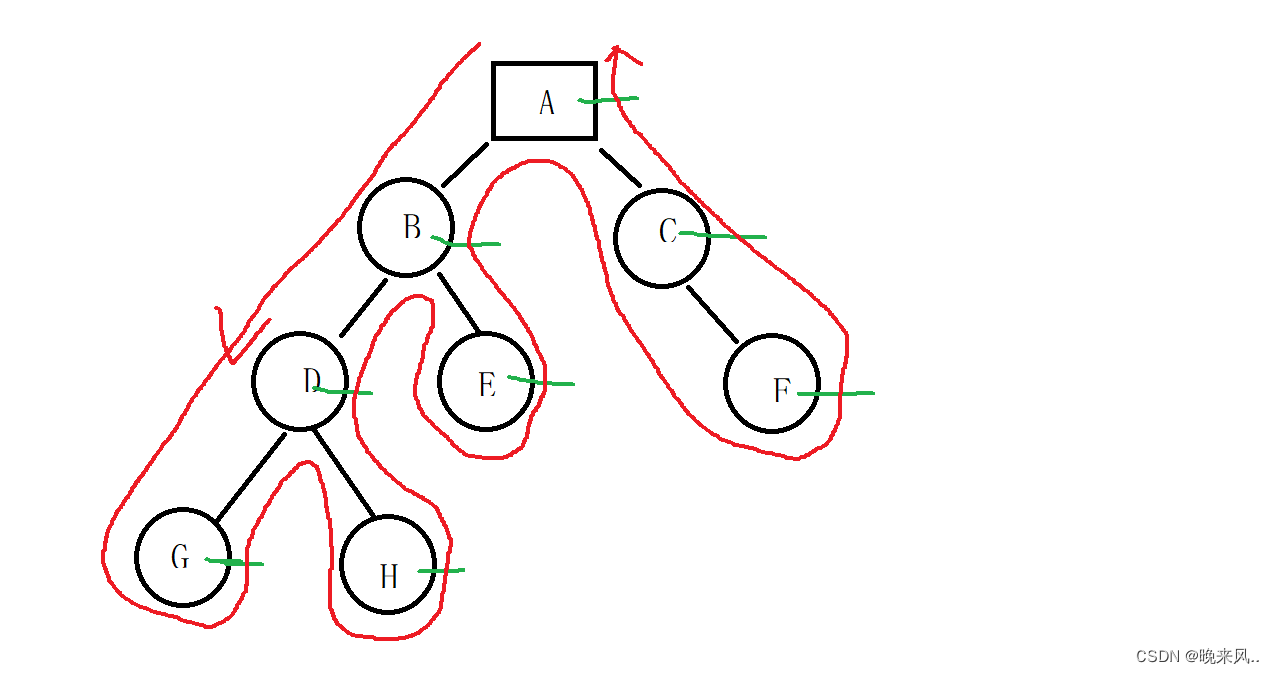
3、后序遍历(RLN)：①先左子树②访问右子树③访问根结点。得到的结果序列是：GHDEBFCA

算法如下：后序遍历是先访问左子树，然后到头，访问头的左子树、右子树、根结点。然后退出最内层递归，执行最内层-1的递归访问右子树......。

void PostOrder(BTree & bt)
{
   PostOrder(bt.r);
}

void PostOrder1(BTree * b)
{
   if(b!=NULL)
      {
        PostOrder1(b->lchild);  //访问左子树
        PostOrder1(b->rchild); //访问右子树
        cout<<b->data; //访问根结点
      }    
}