平衡二叉树平衡二叉树的定义插入删除查找分裂合并

72 阅读 0 评论 48 点赞

我是靠谱客的博主坦率大雁，最近开发中收集的这篇文章主要介绍平衡二叉树平衡二叉树的定义插入删除查找分裂合并，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

平衡二叉树的定义

在学习平衡二叉树之前，需要先了解什么是平衡二叉树，平衡二叉树有哪些特点？平衡二叉树或者是棵空树，或者具有下列性质的二叉查找树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的高度之差的绝对值不超过1，平衡因子的值只可能为-1,0,1。平衡二叉树中最需要注意的就是平衡问题，只要有一个结点的平衡因子的绝对值大于1，那么这棵树就失去了平衡，在插入，删除操作中都可能会出现失衡情况，此时则需要重新调整平衡。

平衡二叉树的存储结构类型：

typedef struct BBSTNode {
	int data;
	int bf;  //结点平衡因子
	struct BBSTNode *lchild, *rchild;
}*BBSTree;

插入

设置高度变化标志taller，taller为TREU时表示被插入结点的子树高度增加，此时需要考虑平衡调整，为FALSE表示高度没有变化。
依次插入结点，有以下几种情况：

（1）平衡二叉树为空树，则插入结点直接作为根结点，树的高度增加taller=TRUE；
（2）待插入结点与平衡二叉树中存在的结点相等，不用插入，taller=FALSE；
（3）若待插入结点小于根结点，且平衡二叉树中不存在与根结点相等的值，在左子树中插入，若插入后左子树的高度增加1。（左子树高度不变则不需要调整平衡）
根据情况判断是否需要平衡调整：
① 原根结点的平衡因子为-1（左高右低），更改为0，树的高度不变。
② 原根结点的平衡因子为0（左右相等），更改为1，树的高度增加1。
③ 原根结点的平衡因子为1（左高右低）：若左子树根结点平衡因子为1，则是LL型失衡，平衡调整修改平衡因子。若左子树根结点平衡因子为-1，则为LR型，平衡调整后修改平衡因子。

假设p是最小失衡树，s是插入的结点

LL型
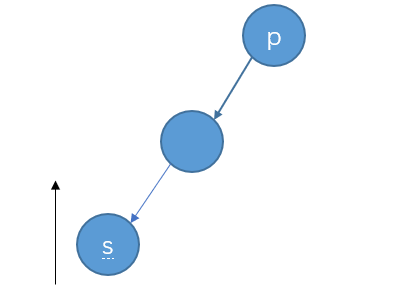
在这里插入图片描述
LR型

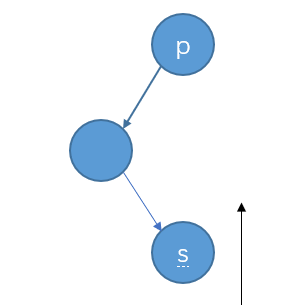
（4）若待插入结点大于根结点，且平衡二叉树中不存在与根结点相等的值，在右子树中插入，若插入后右子树高度加一。（右子树高度不变则不需要调整平衡）
① 原根结点的平衡因子为1（左高右低），更改为0，树的高度不变。
② 原根结点的平衡因子为0（左右相等），更改为-1，树的高度增加1。
③ 原根结点的平衡因子为-1（左低右高）：若右子树根结点平衡因子为1，RL型失衡，平衡调整后修改平衡因子。若右子树根结点平衡因子为-1，RR型失衡，平衡调整后修改平衡因子。
RR型
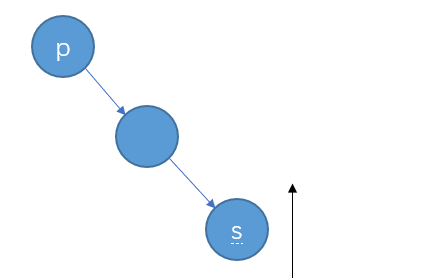
在这里插入图片描述
RL型
、
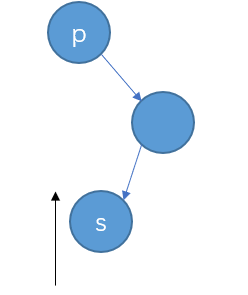代码如下：

Status InsertAVL(BBSTree &T, RcdType e, Status &taller) {
	if (NULL == T) {		//二叉树为空，插入新节点作为根结点
		T = (BBSTree)malloc(sizeof(BBSTNode));
		T->data = e;
		T->bf = EH;
		T->lchild = NULL;
		T->rchild = NULL;
		taller = TRUE;
	}
	else if (e.key == T->data.key) {		//树中已存在和e相等的结点
		taller = FALSE;
		return FALSE;				//未插入，返回FALSE
	}
	else if (e.key < T->data.key) {	//e小于根结点，插入到左子树中
		if (FALSE == InsertAVL(T->lchild, e, taller))	return FALSE;	//递归插入，找到NULL=T的子树插入，若有相等的值返回FALSE
		if (TRUE == taller) {
			switch (T->bf) {			//检查T的平衡因子
			case LH:
				LeftBalance(T);
				taller = FALSE; 
				break;//原左高，做左平衡处理
			case EH:
				T->bf = LH; 
				taller = TRUE; 
				break; //原等高，变成左高
			case RH:
				T->bf = EH;
				taller = FALSE;   //原右高，变成等高
				break;
			}
		}
	}
	else {			//插到右子树中         
		if (FALSE == InsertAVL(T->rchild, e, taller)) return FALSE; //递归插入到右子树，若右子树中有相等的值，返回FALSE
		if (TRUE == taller) { //确认插入
			switch (T->bf) {
			case LH:T->bf = EH; taller = FALSE; break;     //原本左高，插入后变成等高
			case EH:T->bf = RH; taller = TRUE; break;   //原本等高，插入后变成右高
			case RH:RightBalance(T); taller = FALSE; break; //原本右高，插入新节点后失衡，右平衡处理操作，树没有变高
			}
		}
	}
	return TRUE;
}

删除

假设删除的结点为p结点，在进行删除操作之前需要进行查找操作，在平衡二叉树中查找p结点：
（1）p结点小于当前根结点，在根结点的左子树中递归查找p结点。
（2）p结点等于当前根结点，进行删除操作。
（3）p结点大于当前根结点，在根结点的右子树中递归查找p结点。
在平衡二叉树中删除一个结点，有以下三种情况：
（1）p结点是根结点
当p是根结点，也就是没有左右孩子，此时我们删除结点只需要把p直接删除。
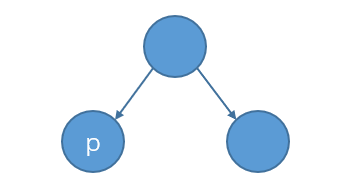
在这里插入图片描述

（2）p结点只有一棵子树
p结点只有左孩子（右孩子）s时，把左孩子（右孩子）s的数据复制给p结点，然后把s结点删除。
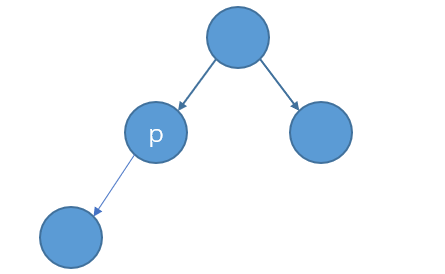
在这里插入图片描述
（3）p结点有两棵子树
p结点既有左孩子又有右孩子时，有两种方法：
a.让p结点左孩子中最大的结点s复制给p结点，然后删除s结点，此时，如果s结点有左孩子，则把左孩子移到s结点的双亲结点上。
b.让p结点右孩子中最小的结点s复制给p结点，然后删除s结点，此时，如果s结点有右孩子，则把右孩子移到s结点的双亲结点上。
一般情况下，在高度较大的子树中实行删除操作，即若左子树比右子树高，执行a方法，若右子树比左子树高，执行b方法。
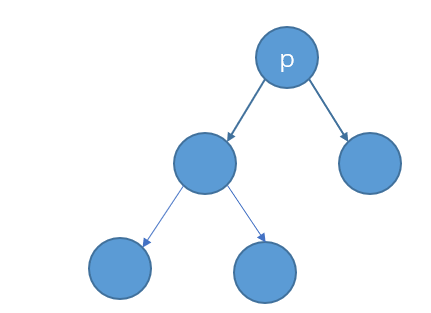
在这里插入图片描述
同样的，平衡二叉树删除一个结点后，也可能会失去平衡。在左子树中删除一个结点相当于在右子树中插入一个结点，这个时候需要利用结点的平衡因子重新调整平衡。
代码如下：

Status Delete(BBSTree &p, int &e, int &flag) {
	BBSTree q, s;
	if (!p->rchild) { //p结点的右子树为空
		q = p;
		if (p->lchild) {  //情况3，p结点的左子树不为空，用左子树最大的结点代替p结点的位置
			p->lchild->bf = p->bf;
			e = p->lchild->data.key;
		}
		p = p->lchild; //把左子树结点的值复制给p结点，若是左子树为空，则是情况1
		free(q);     //删除p结点内存
		flag = 1;
	}
	else if (!p->lchild) { //情况2，p结点左子树为空，右子树不为空的情况
		q = p;
		p->rchild->bf = p->bf;
		e = p->rchild->data.key;
		p = p->rchild;
		free(q);
		flag = 1;
	}
	else {    //情况4，有左右子树的情况
		q = p;
		s = p->lchild;
		while (s->rchild) { //若p的左子树s有右子树
			q = s;          //q则是最大结点的双亲   
			s = s->rchild; //使s成为左子树内最大的结点，只能是叶子结点或者一个没有右孩子的结点
		}
		p->data.key = s->data.key; //把最大结点的数值复制给p结点
		if (q != p) {  //若p的左子树有右子树，找到右子树的最大值和p结点交换  s->rchild ！= NULL 的情况
			q->rchild = s->lchild;
		}
		else {		//若p的左子树没有右子树时  s->lchild==NULL
			q->lchild = s->lchild;  //若p的左子树没有右子树，p==q
			p->bf = RH;
		}
		e = p->data.key;
		free(s);
	}
	return TRUE;
}

查找

平衡二叉树的查找也是利用递归算法实现，因为平衡二叉树是特殊的二叉查找树，当查找值e小于当前根节点时，在左子树中递归查找。当查找值e大于当前根结点时，在右子树中递归查找。
代码如下：

Status SearchAVLNode(BBSTree T, KeyType key) {
	if (!T) return ERROR;
	if (T->data.key == key) {
		printf("查询结果：%d，平衡因子：%dn", T->data.key, T->bf);
		return OK;
	}
	else {
		if (T->lchild)      //在左子树中查找
			if (SearchAVLNode(T->lchild, key)) //递归
				return OK;
		if (T->rchild)		//在右子树中查找
			if (SearchAVLNode(T->rchild, key)) //递归
				return OK;
		return ERROR;
	}
}

分裂

利用递归算法，需要先输入关键字key，在平衡二叉树中，结点数据比key小的值依次插入到T1，结点数据比key大的值依次插入到T2。也就是说分裂出来的两棵子树，一棵比key大，一棵比key小。

代码如下：

Status Split(BBSTree T, KeyType e, BBSTree &T1, BBSTree &T2) {
	Status taller = 0;
	if (!T) return TRUE;
	Split(T->lchild, e, T1, T2);
	if (T->data.key > e) {
		InsertAVL(T2, T->data, taller);
	}else {
		InsertAVL(T1, T->data, taller);
	}
	Split(T->rchild, e, T1, T2);
	return TRUE;
}

合并

平衡二叉树的合并操作也是利用递归算法实现，假如需要合并T1,T2，在T1中递归插入T2的结点，就能实现合并操作,其核心算法还是插入操作。

代码如下：

Status MergeAVL(BBSTree &T1, BBSTree &T2) {
	Status taller;
	if (!T2) return TRUE;
	if (T2->lchild) MergeAVL(T1, T2->lchild);    //T2左子树结点插入T1中
	if (T2->rchild) MergeAVL(T1, T2->rchild);    //T2右子树结点插入T2中
	if (!InsertAVL(T1, T2->data, taller)) return FALSE;
	return TRUE;
}