引言
之前写了两个关于粒子群实现配电网重构的文章,很多同学私信我配电网重构相关的知识,配电网重构的难点就在于网络的联通和辐射,之前的文章中粒子群算法很便捷的实现了这个功能,那么如果通过规划算法来实现重构就是本次文章深入探讨的东西,文章还专门分析了sop的创建方式,具体文章可参考《高比例新能源下考虑需求侧响应和智能软开关的配电网重构》,希望同大家共同讨论。
目录
引言
一 模型
1.1 sop模型
1.2 混合整数二阶锥规划MISOCP
1.3 连通性和辐射性讨论
二 现有程序效果
三 程序链接
一 模型
1.1 sop模型


1.2 混合整数二阶锥规划MISOCP
目标函数可设定为切负荷最少+网损最小等,可根据实际情况自行设定,下面代码展示以切负荷和网损的权值多目标作为目标的matlab程序。
f=w1*r_ij'*x_Iij_square(:,opt_num)+w2*sum(p_load)+w2*sum(-lamda.*p_load);约束条件:
(1)潮流约束
Distflow 潮流模型[23] 是一种从支路功率出发建 立的潮流方程,相比于传统的基于节点功率的潮流计算法,Distflow 潮流模型更适用于辐射状配电系统的潮流计算。由于在配电网重构中网络拓扑的不断变化,考虑配电网重构特性,假定配电系统中所有的开关均闭合,配电网重构问题相当于选择其中部分开关断开的问题,对传统 Distflow 潮流模型进行改进,通过引入线路开断变量 αij 对潮流方程进行松弛 ,具体模型如下:

具体程序代码段:
%欧姆定律约束
m = (1.05*1.05 - 0.95*0.95)*12.66^2;
M = (ones(nl,1) - Zij)*m;
Constraints = [Constraints, x_ui_square(Branch(:,2),:) - x_ui_square(Branch(:,3),:) <= M - (r_ij.^2+x_ij.^2).*x_Iij_square(:,opt_num)+...
2*(r_ij.*x_pij(:,opt_num)+x_ij.*x_qij(:,opt_num))];
Constraints = [Constraints, x_ui_square(Branch(:,2),:) - x_ui_square(Branch(:,3),:) >= -M - (r_ij.^2+x_ij.^2).*x_Iij_square(:,opt_num)+...
2*(r_ij.*x_pij(:,opt_num)+x_ij.*x_qij(:,opt_num))];(2)节点电压和电流约束

这个约束比较简单,再此不再单独附代码段。
(3)SOP约束
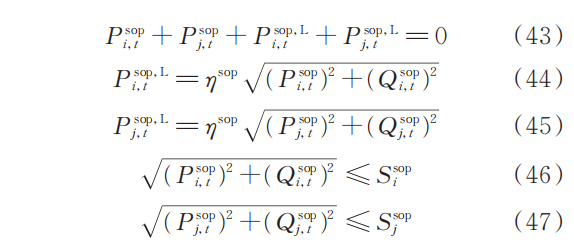
Constraints=[Constraints,x_p_sop1(1,opt_num)+x_p_sop1(2,opt_num)==0,x_q_sop1(1,opt_num)+x_q_sop1(2,opt_num)==0];
Constraints=[Constraints,x_p_sop1(1,opt_num)^2+x_q_sop1(1,opt_num)^2<=S_sopi1];(4)配电系统连通性和辐射性约束
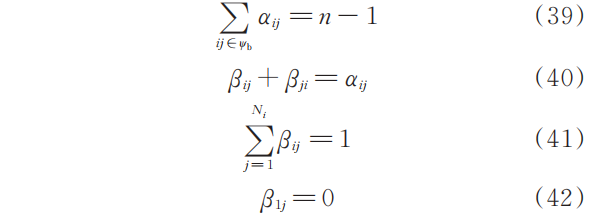
1.3 连通性和辐射性讨论
配电网的连通性和辐射性采用图论的方式进行约束,上面给出了约束表达方式,但是原始文献中给出的表达式更加清晰准确(Mathematical representation of radiality constraint in distribution system reconfiguration problem):

这里面对网络参数的限定更加准确一些,而且文章中对于过程推导也很详实,并且说明了一个观点:配电网络的连通性是由潮流进行限定的,也就是说上述的约束就是为了保证网络的辐射性,具体代码如下:
dd = binvar(37,2);
for i=1:37
Constraints=[Constraints,sum(dd(i,:))==1,
implies(dd(i,1),[Zij(i)==0,beta(Branch(i,2),Branch(i,3))==0,beta(Branch(i,3),Branch(i,2))==0]),%非联通情况下的参数关系
implies(dd(i,2),[Zij(i)==1,beta(Branch(i,2),Branch(i,3))+beta(Branch(i,3),Branch(i,2))==1])];%联通情况下的参数关系
end
for i=1:37
for j=1:37
if ~ismember([i,j],Branch(:,[2,3]))
Constraints=[Constraints,beta(i,j)==0];%非联通节点的参数beta设置为0
end
end
end
Constraints=[Constraints,sum(beta(1:37,:),2)==1];%公式6c
Constraints=[Constraints,beta(1,2)==0];%公式6d二 现有程序效果
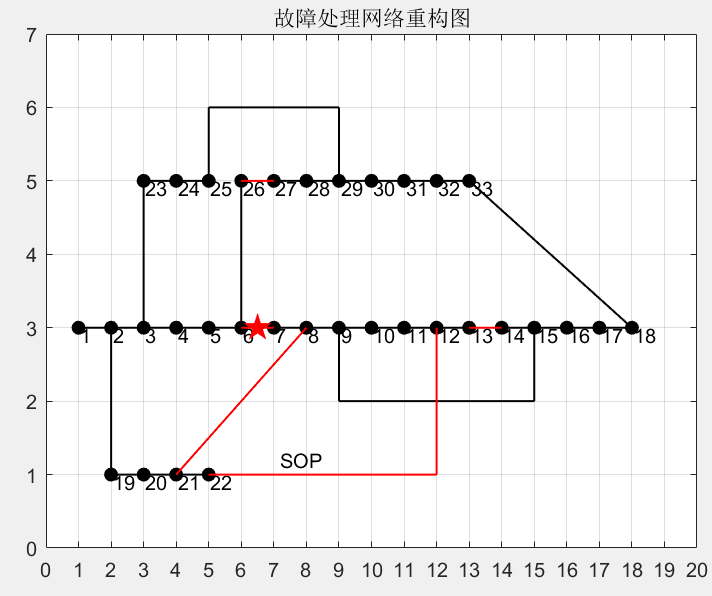
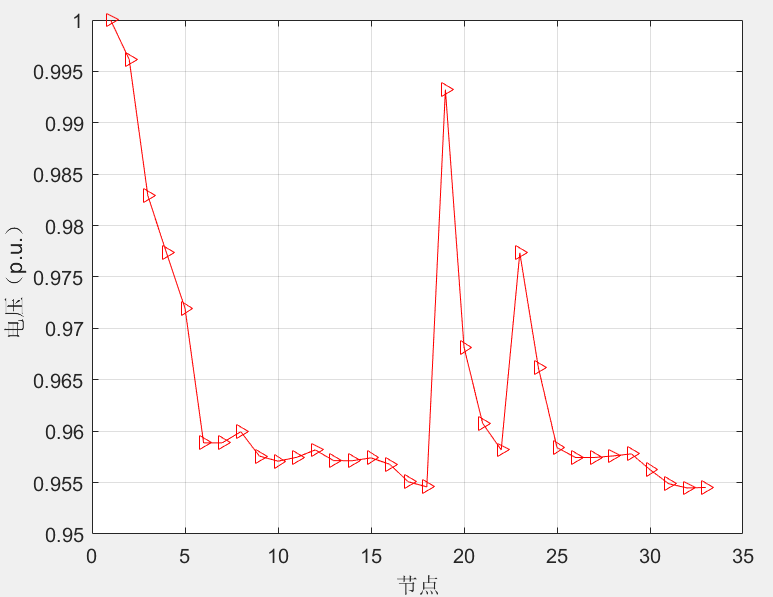
通过以上理论分析,将方法应用于33节点网络的配电网重构中,线路6-7故障情况下得到的网络重构图和电压效果图如下所示。
三 程序链接
见评论区置顶评论!
最后
以上就是贤惠刺猬最近收集整理的关于配电网重构之二阶锥模型引言一 模型二 现有程序效果三 程序链接的全部内容,更多相关配电网重构之二阶锥模型引言一内容请搜索靠谱客的其他文章。








发表评论 取消回复