A Simple Chess(容斥+Lucas定理)

原题：hdu 5794

题意：

由(1,1)走到(n,m)每次只能往右上方走两种“日”型（象棋），其他有r个点是不能走的，求方案数。

解析：

方便起见，把所有坐标减1

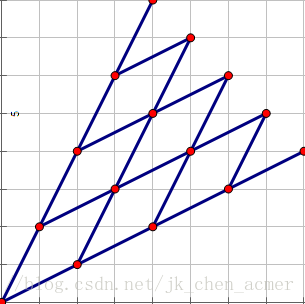
分析一下可以走到的点，发现x+y=3k，并且x>=k,y>=k

我们以y=x/2为新的x轴，y=2x为新的y轴重构，得到y=y-k，x=x-k，例如图中(4,5)变成了(1,2)，(4,2)变成了(2,0)

那么题目变成了n*m方格由(0,0)走到(n,m)，每次可以往上或往下的方案数

(0,0)到(n,m)的方案数为$C_{n+m}^n$

首先处理出从起点到所有的不能走的点和终点的距离，再容斥出每个点的dp值（dp[i]=j表示从起点到i点没有经过其他不可走的点的方案数）

怎么容斥呢？走到一个点i，不经过其他点的方案数=总方案数-$sum$（不经过其他点走到k的方案数 * k到i的方案数）这样子保证了所有的方案数不会重复，因为经过的第一个点都是不同的，方案之间显然是不同的

这道题我本来是想要先处理掉不合法（不能从起点到这个点，或是不能从这个点到终点）的点的，但是一直WA，现在也搞不清楚为什么，无奈。
$\$
还有之前没有读入完全就可以判断终点非法，我直接continue了，导致r变成1e18了一直T，QAQ

#include<iostream>
#include<algorithm>
#include<map>
using namespace std;
#define LL long long
const LL mod=110119;
#define random(a,b) (rand()%(b-a+1)+a)
#define pill pair<long long,long long>
#define mk make_pair
LL read(){
    LL t;scanf("%lld",&t);return t;
}

LL fac[mod+2];
void init(){
    fac[0]=fac[1]=1;
    for(int i=2;i<mod;i++)fac[i]=fac[i-1]*i%mod;
}

LL sw(LL a,LL b){
    a%=mod;
    LL ans=1;
    while(b){
        if(b&1)ans=ans*a%mod;
        b>>=1;a=a*a%mod;
    }return ans;
}
LL C(LL n,LL m){
    if(m>n||m<0||n<0)return 0;
    return fac[n]*sw(fac[m]*fac[n-m],mod-2)%mod;
}

LL lucas(LL n,LL m){
    if(m==0)return 1ll;
    return C(n%mod,m%mod)*lucas(n/mod,m/mod)%mod;
}

///////////////////////////////////////////////////////////////////////
LL n,m,r;
struct node{
    LL x,y;
    bool operator<(const node &a)const{
        return y+x<a.y+a.x;
    }
}e[109];

int check(LL x,LL y){
    x--,y--;
    LL _=(x+y)/3;
    if((x+y)%3||x<_||y<_)return 0;
    return 1;
}
LL cal(LL A,LL B,LL a,LL b){
    if(!check(a,b)) return 0;
    if(!check(A,B)) return 0;

    A--,B--,a--,b--;//变到新的坐标系里面计算
    LL _=(A+B)/3;
    A-=_,B-=_;
    _=(a+b)/3;
    a-=_,b-=_;
    if(A>a||B>b)return 0;
    return lucas(a-A+b-B,a-A);
}
LL dp[109];



int main(){
    int ca=0;
    init();

    while(scanf("%lld%lld%lld",&n,&m,&r)!=EOF){
        for(int i=1;i<=r;i++)scanf("%lld %lld",&e[i].x,&e[i].y);
        sort(e+1,e+1+r);
        e[++r].x=n,e[r].y=m;
        printf("Case #%d: ",++ca);

        if(!check(n,m)){printf("0n");continue;}

        for(int i=1;i<=r;i++)
        {
            dp[i]=cal(1,1,e[i].x,e[i].y);
            for(int j=1;j<i;j++)
                dp[i]=(dp [i]-dp[j]*cal(e[j].x,e[j].y,e[i].x,e[i].y)%mod+mod)%mod;
        }
        printf("%lldn",dp[r]);

    }
}

最后

以上就是成就溪流为你收集整理的A Simple Chess(容斥+Lucas定理)的全部内容，希望文章能够帮你解决A Simple Chess(容斥+Lucas定理)所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。