白话机器学习算法理论+实战之朴素贝叶斯

1. 写在前面

如果想从事数据挖掘或者机器学习的工作，掌握常用的机器学习算法是非常有必要的，比如我之前写过的一篇十大机器学习算法的小总结，在这简单的先捋一捋， 常见的机器学习算法：

• 监督学习算法：逻辑回归，线性回归，决策树，朴素贝叶斯，K近邻，支持向量机，集成算法Adaboost等
• 无监督算法：聚类，降维，关联规则, PageRank等

为了详细的理解这些原理，曾经看过西瓜书，统计学习方法，机器学习实战等书，也听过一些机器学习的课程，但总感觉话语里比较深奥，读起来没有耐心，并且理论到处有，而实战最重要， 所以在这里想用最浅显易懂的语言写一个白话机器学习算法理论+实战系列。

个人认为，理解算法背后的idea和使用，要比看懂它的数学推导更加重要。idea会让你有一个直观的感受，从而明白算法的合理性，数学推导只是将这种合理性用更加严谨的语言表达出来而已，打个比方，一个梨很甜，用数学的语言可以表述为糖分含量90%，但只有亲自咬一口，你才能真正感觉到这个梨有多甜，也才能真正理解数学上的90%的糖分究竟是怎么样的。如果这些机器学习算法是个梨，本文的首要目的就是先带领大家咬一口。
另外还有下面几个目的：

• 检验自己对算法的理解程度，对算法理论做一个小总结
• 能开心的学习这些算法的核心思想， 找到学习这些算法的兴趣，为深入的学习这些算法打一个基础。
• 每一节课的理论都会放一个实战案例，能够真正的做到学以致用，既可以锻炼编程能力，又可以加深算法理论的把握程度。
• 也想把之前所有的笔记和参考放在一块，方便以后查看时的方便。

学习算法的过程，获得的不应该只有算法理论，还应该有乐趣和解决实际问题的能力！

今天是白话机器学习算法理论+实战的第五篇，朴素贝叶斯算法，这个算法最适合的场景就是文本分类任务了，常用语自然语言处理任务，但可不单单是用于文本分类，贝叶斯方法被证明是非常general且强大的推理框架，通过今天的学习，快速掌握朴素贝叶斯的计算原理和工作流程，并且运用学习到的原理和流程，做一个文本分类的任务。

大纲如下：

• 贝叶斯原理（不要畏惧不可知，要从已知推未知）
• 朴素贝叶斯分类的工作原理（离散数据和连续数据案例）
• 朴素贝叶斯分类实战（文本分类，在这里会掌握TF-IDF技术，会认识分词技术）

OK, let’s go !

2. 朴素贝叶斯？ 还是先从贝叶斯原理开始吧！

很多人都听说过贝叶斯原理？ 在哪？ 当然是在学概率统计的时候了，有些人可能会说，完蛋， 概率统计的知识都忘光了， 哈哈， 那也没有关系， 谁让这里是白话机器学习算法呢， 肯定是大白话的学习算法精华啊。 在这之前，得需要了解一下贝叶斯原理， 放心，这里没有复杂的公式，只需要一个小例子，你就发现，不知不觉的就学到了贝叶斯原理的核心思想，对，就是这么神奇。 不信？ 那就接着往下看。

贝叶斯原理是英国数学家托马斯·贝叶斯提出的。贝叶斯是个很神奇的人，他的经历类似梵高。生前没有得到重视，死后，他写的一篇关于归纳推理的论文被朋友翻了出来，并发表了。这一发表不要紧，结果这篇论文的思想直接影响了接下来两个多世纪的统计学，是科学史上著名的论文之一。（哈哈，厉害吧，只可惜，贝叶斯看不见了）

贝叶斯原理是怎么来的呢？ 贝叶斯为了解决一个叫“逆向概率”问题写了一篇文章，尝试解答在没有太多可靠证据的情况下，怎样做出更符合数学逻辑的推测。这里有个词，叫做逆向概率。 What is “逆向概率”?

所谓“逆向概率”是相对“正向概率”而言。

正向概率总知道吧， 比如，一个袋子里5个球， 3个黑球，2个白球，我随便从里面拿出一个，问，是黑球的概率？。 这时候，立即答：3/5。

哈哈，这就是正向概率了，很容易理解吧，但这种情况往往是上帝的视角，即了解了事情的全貌做的判断（事先知道了袋子里有5个球）。

But, 如果我们事先只知道，袋子里不是黑球就是白球，并不知道各自有多少个，而是通过我们摸出的球的颜色，我们能判断出袋子里黑白球各自多少个来吗？ 这就是逆向概率了。

正是这样一个普普通通的问题，影响了接下来近 200 年的统计学理论。这是因为，贝叶斯原理与其他统计学推断方法截然不同，它是建立在主观判断的基础上：在我们不了解所有客观事实的情况下，同样可以先估计一个值，然后根据实际结果不断进行修正。

好吧， 猜你现在正迷糊呢！ 看个简单的例子吧，让你不知不觉的就爱上贝叶斯，哦，原理：

一所学校里面有 60% 的男生，40% 的女生。男生总是穿长裤，女生则一半穿长裤一半穿裙子。有了这些信息之后我们可以容易地计算“随机选取一个学生，他（她）穿长裤的概率和穿裙子的概率是多大”，这个就是前面说的“正向概率”的计算。

然而，假设你走在校园中，迎面走来一个穿长裤的学生（很不幸的是你高度近视，你只看得见他（她）穿的是否长裤，而无法确定他（她）的性别），你能够推断出他（她）是男生的概率是多大吗？

看上面这个例子，你能算出来吗？ 好像涉及到逆向推理了来。

我们可能对形式化的这种贝叶斯问题不擅长，但是我们对数形式的等价问题应该很擅长，在这里，不妨把问题换一下子： 你在校园里随机游走，遇到了N个长裤的人（仍然看不清性别）， 问，这N个人里面有多少个男生，多少个女生？

你说，这还不简单？ 算出学校里有多少个穿长裤的，然后在这些人里，再算出多少女生，多少男生不就行了？

哈哈，厉害，那么我们就一起算一下吧：
假设，学校里面有M个人。

1. 首先，先算算，这个学校有多少男的，多少女的

   60%的男生，40%的女生，则男生的个数是$M\ast P(男)$， 女生的个数$M\ast P(女)$。 这没问题吧？

2. 那我们再算算，男生里面，穿长裤的有多少人？

   根据上面我们知道，男生都穿长裤，也就是只要是男的，他就穿长裤（你发现了吗？ 这里有个词，前提是男的，这是个什么？ 对，条件概率）， 即$P(长裤|男）=100$。
   
   那么，穿长裤的男生的个数就等于：男生的个数乘以前面的概率 = $M\ast P(男)\ast P(长裤|男）$

3. 同理， 我们算一下，女生里面，穿长裤的多少人？

   根据上面我们知道，女生里面，有一半的人穿长裤，一般的人穿裙子，也就是P(长裤 | 女) = 50%, 这个也是个条件概率了，因为前提是女的。
   
   那么，穿长裤的女生的个数就等于： $M\ast P(女)\ast P(长裤|女)$

4. 这就成了，那么这个学校里面，穿长裤的人就是穿长裤的男生+长裤的女生

   穿长裤的人 = $M\ast P(男)\ast P(长裤|男）+M\ast P(女)\ast P(长裤|女)$

5. 那么穿长裤的这里面，男生和女生的比例是多少呢？

   穿长裤的这里面， 男生的比例应该这样计算（注意，这里发现改变条件了吗？ 前提是穿长裤了），即P(男 | 长裤）和P(女 | 长裤)。
   
   怎么算呢？ 简单，总的穿长裤的人知道，又知道，长裤的男的和女的各自的数量，那么：
   

   • $P(男|长裤）=\frac{M\ast P(男)\ast P(长裤|男)}{M\ast P(男)\ast P(长裤|男）+M\ast P(女)\ast P(长裤|女)}$
   • $P(女|长裤)=\frac{M\ast P(女)\ast P(长裤|女)}{M\ast P(男)\ast P(长裤|男）+M\ast P(女)\ast P(长裤|女)}$

6. 上面的式子，发现分子分母，都有M，约掉，就变成了

   • $P(男|长裤）=\frac{P(男)\ast P(长裤|男)}{P(男)\ast P(长裤|男）+P(女)\ast P(长裤|女)}$
   • $P(女|长裤)=\frac{P(女)\ast P(长裤|女)}{P(男)\ast P(长裤|男）+P(女)\ast P(长裤|女)}$

其实，这个例子到这就结束了，这就是最上面的那个问题的答案。我先不说，上面这个公式是个什么东西？ 我得先保证你能看明白上面这个例子， 如果看不明白，我先解释几个概念：

• 先验概率：通过经验来判断事情发生的概率就是先验概率。 比如上面的男生60%， 女生40%。 这就是个事实，不用任何条件。 再比如，南方的梅雨季是6-7月，就是通过往年的气候总结出来的经验，这个时候下雨的概率比其他时间高出很多，这些都是先验概率。
• 条件概率： 事件 A 在另外一个事件 B 已经发生条件下的发生概率，表示为 P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。比如上面的男生里面，穿长裤的P(长裤 | 男)，女生里面，穿长裤的人P(长裤 | 女)。
• 后验概率： 后验概率就是发生结果之后，推测原因的概率。比如上面的我看到了穿长裤的人， 我推测这是个男人P(男 | 长裤）还是个女人P(女 | 长裤)的概率。 它属于条件概率的一种。

上面的三个概率懂了吗？可以测试一下：

如果你的女朋友，在你的手机里发现了和别的女人的暧昧短信，于是她开始思考了 3 个概率问题，你来判断下下面的 3 个概率分别属于哪种概率：

• 你在没有任何情况下，出轨的概率；
• 如果你出轨了，那么你的手机里有暧昧短信的概率；
• 在你的手机里发现了暧昧短信，认为你出轨的概率。

上面这三种概率能对号入座了吗？ 如果能，说明你懂了上面的概念，也弄了上面的例子，下面开始说正事。

我们再把上面例子中最后的概率写到下面：

• $P(男|长裤）=\frac{P(男)\ast P(长裤|男)}{P(男)\ast P(长裤|男）+P(女)\ast P(长裤|女)}$
• $P(女|长裤)=\frac{P(女)\ast P(长裤|女)}{P(男)\ast P(长裤|男）+P(女)\ast P(长裤|女)}$

这里的$P(男)$， $P(女)$就是先验概率；$P(长裤|男)$，$P(长裤|女)$就是条件概率；$P(男|长裤)$，$P(女|长裤)$就是后验概率。

上面长裤和男女可以指代一切东西，令$长裤=A,男=B1,女=B2$, 那么整理一下上面的公式：
$$P\left(B_i\mid A\right)=\frac{P\left(B_i\right)P\left(A\mid B_i\right)}{P\left(B_1\right)P\left(A\mid B_1\right)+P\left(B_2\right)P\left(A\mid B_2\right)}$$
这个，就是伟大的贝叶斯公式。 下面这个是更通用的形式：
$$P\left(B_i\mid A\right)=\frac{P\left(B_i\right)P\left(A\mid B_i\right)}{{\sum }_{i=1}^{n}P\left(B_i\right)P\left(A\mid B_i\right)}$$
难怪拉普拉斯说概率论只是把常识用数学公式表达了出来。

实际上，贝叶斯原理就是求解后验概率。 通过啥？ 贝叶斯公式。

现在，是不是感觉，没有烧多少脑就理解了贝叶斯原理了。这就说明，如果我们遇到一个不知道的条件概率的计算，我们要通过贝叶斯公式进行转换，不要畏惧不可知，要从已知推未知。

然而，看似这么平凡的贝叶斯公式，背后却隐含着非常深刻的原理。

在这里我不多说，怕你犯困，如果感兴趣，见我后面那篇经典博客：通俗易懂讲解贝叶斯。 因为我的目的，不仅是理解原理，还得实战会用。这里没有完全理解也不怕，下面讲朴素贝叶斯，我还会实例运算一波。

3. 朴素贝叶斯

讲完贝叶斯原理之后，我们再来看下重点要说的算法，朴素贝叶斯。

它是一种简单但极为强大的预测建模算法。之所以称为朴素贝叶斯，是因为它假设每个输入变量是独立的。这是一个强硬的假设，实际情况并不一定，但是这项技术对于绝大部分的复杂问题仍然非常有效。

这里的输入变量是啥？ 就类似与我们上面的性别特征，因为实际问题里面，可能不仅只有性别这一列特征，可能还会有什么身高啊，体重啊，这些特征，基于这些特征再利用贝叶斯公式去做分类问题的时候，就涉及很多个输入特征了。

朴素贝叶斯做的就是，假设这些身高，体重，性别这些特征之间是没有关系的，互相不影响。那么我们算同时符合这三个特征概率的时候，就可以分开算了$P(ABC)=P(A)\ast P(B)\ast P(C)$就是这个道理了。

朴素贝叶斯模型由两种类型的概率组成：

• 每个类别的概率$P(C_j)$；
• 每个属性的条件概率$P(A_i|C_j)$。

再举个例子说明一下类别概率和条件概率：

假设我有 7 个棋子，其中 3 个是白色的，4 个是黑色的。那么棋子是白色的概率就是 3/7，黑色的概率就是 4/7，这个就是类别概率。


假设我把这 7 个棋子放到了两个盒子里，其中盒子 A 里面有 2 个白棋，2 个黑棋；盒子 B 里面有 1 个白棋，2 个黑棋。那么在盒子 A 中抓到白棋的概率就是 1/2，抓到黑棋的概率也是 1/2，这个就是条件概率，也就是在某个条件（比如在盒子 A 中）下的概率。


假设，我取出来的是白色的棋子，我问，属于A盒子的概率？ 你会算吗？

不会？ 上面的贝叶斯公式白学了！

贴出计算过程：

为了训练朴素贝叶斯模型，我们需要先给出训练数据，以及这些数据对应的分类。那么上面这两个概率，也就是类别概率和条件概率。他们都可以从给出的训练数据中计算出来。一旦计算出来，概率模型就可以使用贝叶斯原理对新数据进行预测。（后面会有案例）

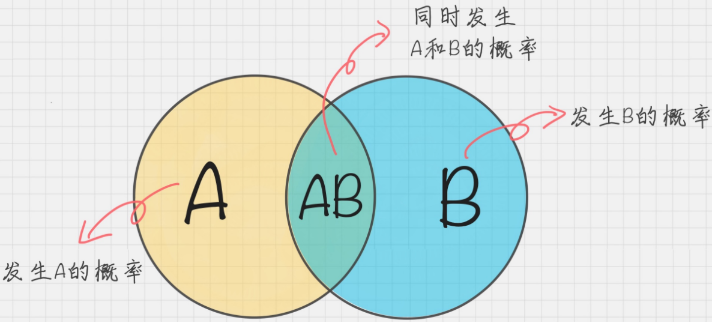
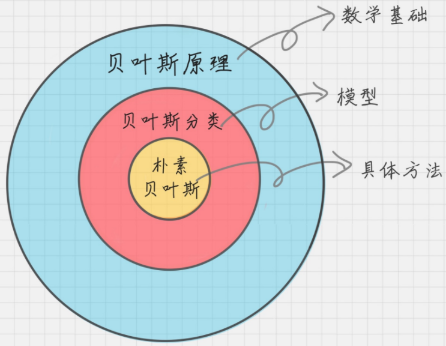
另外，之前还要注意一下，贝叶斯原理，贝叶斯分类和朴素贝叶斯并不是一回事：

贝叶斯原理是最大的概念，它解决了概率论中“逆向概率”的问题，在这个理论基础上，人们设计出了贝叶斯分类器，朴素贝叶斯分类是贝叶斯分类器中的一种，也是最简单，最常用的分类器。朴素贝叶斯之所以朴素是因为它假设属性是相互独立的，因此对实际情况有所约束，如果属性之间存在关联，分类准确率会降低。不过好在对于大部分情况下，朴素贝叶斯的分类效果都不错。

好了，明白了朴素贝叶斯之后，我们两个案例，再来体会一下朴素贝叶斯的计算过程吧（关于朴素贝叶斯的详细推导公式，可以看我下面统计学习方法的笔记）

4. 朴素贝叶斯分类的工作原理

朴素贝叶斯分类是常用的贝叶斯分类方法。我们日常生活中看到一个陌生人，要做的第一件事情就是判断 TA 的性别，判断性别的过程就是一个分类的过程。根据以往的经验，我们通常会从身高、体重、鞋码、头发长短、服饰、声音等角度进行判断。这里的“经验”就是一个训练好的关于性别判断的模型，其训练数据是日常中遇到的各式各样的人，以及这些人实际的性别数据。

4.1 离散数据案例

我们遇到的数据可以分为两种，一种是离散数据，另一种是连续数据。那什么是离散数据呢？离散就是不连续的意思，有明确的边界，比如整数 1，2，3 就是离散数据，而 1 到 3 之间的任何数，就是连续数据，它可以取在这个区间里的任何数值。

我以下面的数据为例，这些是根据你之前的经验所获得的数据。然后给你一个新的数据：身高“高”、体重“中”，鞋码“中”，请问这个人是男还是女？

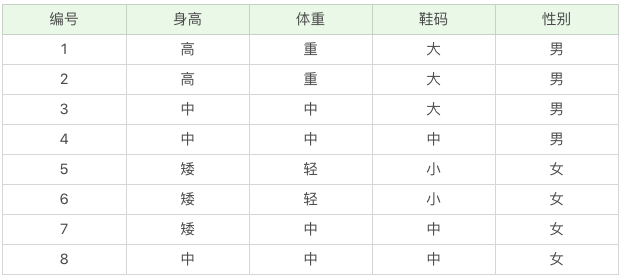
看这个题吧，根据这个题，才可以看出朴素贝叶斯的朴素之地。
下面贴出这个题的过程：

4.2 连续数据案例

实际生活中我们得到的是连续的数值，比如下面这组数据：

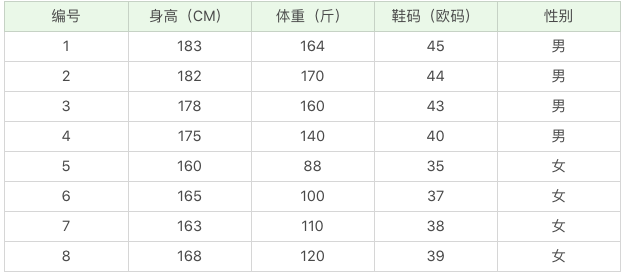
那么如果给你一个新的数据，身高 180、体重 120，鞋码 41，请问该人是男是女呢？

公式还是上面的公式，这里的困难在于，由于身高、体重、鞋码都是连续变量，不能采用离散变量的方法计算概率。而且由于样本太少，所以也无法分成区间计算。怎么办呢？

这时，可以假设男性和女性的身高、体重、鞋码都是正态分布，通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，算出某一点的密度函数的值。（求连续型随机变量在某一个取值点的概率的时候，可以看当前概率密度函数在该点的函数值，值越大，概率越大。 但当前概率密度函数的值不和概率相等，只可以比大小用）

比如，男性的身高是均值 179.5、标准差为 3.697 的正态分布。所以男性的身高为 180 的概率为 0.1069。

这怎么算的？ 这里需要用到工具了， Excel的一个函数：

NORMDIST(x, mean, standard_dev, cumulative)

• x：正态分布中，需要计算的数值；
• Mean：正态分布的平均值；
• Standard_dev：正态分布的标准差；
• Cumulative：取值为逻辑值，即 False 或 True。它决定了函数的形式。当为 TRUE 时，函数结果为累积分布（标准正态）；为 False 时，函数结果为概率密度。

这里我们使用的是NORMDIST(180,179.5,3.697,0)=0.1069。
同理我们可以计算得出男性体重为 120 的概率为 $0.000382324$，男性鞋码为 41 号的概率为 $0.120304111$。

所以我们可以计算得出：$$P(A1A2A3|C1)=P(A1|C1)P(A2|C1)P(A3|C1)=0.1069\ast 0.000382324\ast 0.120304111=4.9169e-6$$

同理我们也可以计算出来该人为女的可能性：$$P(A1A2A3|C2)=P(A1|C2)P(A2|C2)P(A3|C2)=0.00000147489\ast 0.015354144\ast 0.120306074=2.7244e-9$$

很明显这组数据分类为男的概率大于分类为女的概率。

哈哈，是不是计算原理很简单啊。 下面就要检验是不是真的掌握了， 要用朴素贝叶斯进行一个实战，在实战之前，先贴出朴素贝叶斯分类器的工作流程：

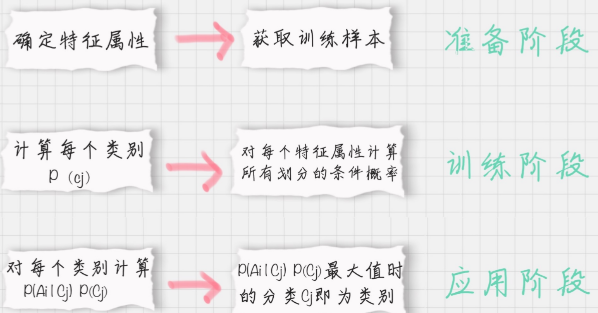
5. 朴素贝叶斯之文本分类

朴素贝叶斯分类常用于文本分类，尤其是对于英文等语言来说，分类效果很好。它常用于垃圾文本过滤、情感预测、推荐系统等。

但是在分类之前，有必要介绍一些文本处理的和模型的知识。

5.1 sklearn中的朴素贝叶斯

sklearn 的全称叫 Scikit-learn，它给我们提供了 3 个朴素贝叶斯分类算法，分别是高斯朴素贝叶斯（GaussianNB）、多项式朴素贝叶斯（MultinomialNB）和伯努利朴素贝叶斯（BernoulliNB）。

这三种算法适合应用在不同的场景下，我们应该根据特征变量的不同选择不同的算法：

• 高斯朴素贝叶斯：特征变量是连续变量，符合高斯分布，比如说人的身高，物体的长度。
• 多项式朴素贝叶斯：特征变量是离散变量，符合多项分布，在文档分类中特征变量体现在一个单词出现的次数，或者是单词的 TF-IDF 值等。
  注意， 多项式朴素贝叶斯实际上符合多项式分布，不会存在负数，所以传入输入的时候，别用StandardScaler进行归一化数据，可以使用MinMaxScaler进行归一化
• 伯努利朴素贝叶斯：特征变量是布尔变量，符合 0/1 分布，在文档分类中特征是单词是否出现。
  
  
  伯努利朴素贝叶斯是以文件为粒度，如果该单词在某文件中出现了即为 1，否则为 0。而多项式朴素贝叶斯是以单词为粒度，会计算在某个文件中的具体次数。而高斯朴素贝叶斯适合处理特征变量是连续变量，且符合正态分布（高斯分布）的情况。比如身高、体重这种自然界的现象就比较适合用高斯朴素贝叶斯来处理。而文本分类是使用多项式朴素贝叶斯或者伯努利朴素贝叶斯。

5.2 什么是TF-IDF值呢？

这一个解释起来，篇幅很多，在这里不单独解释，请移步参考我的另一篇博客：TF-IDF? 这一篇就够了
下面，主要是讲一下，怎么用工具实现这个步骤。

5.3 如何求 TF-IDF？

在 sklearn 中我们直接使用 TfidfVectorizer 类，它可以帮我们计算单词 TF-IDF 向量的值。在这个类中，取 sklearn 计算的对数 log 时，底数是 e，不是 10。

如何创建TfidfVectorizer类呢？

TfidfVectorizer(stop_words=stop_words, token_pattern=token_pattern)

我们在创建的时候，有两个构造参数，可以自定义停用词 stop_words 和规律规则 token_pattern。需要注意的是传递的数据结构，停用词 stop_words 是一个列表 List 类型，而过滤规则 token_pattern 是正则表达式。

什么是停用词？停用词就是在分类中没有用的词，这些词一般词频 TF 高，但是 IDF 很低，起不到分类的作用。为了节省空间和计算时间，我们把这些词作为停用词 stop words，告诉机器这些词不需要帮我计算。

当我们创建好 TF-IDF 向量类型时，可以用 fit_transform 帮我们计算，返回给我们文本矩阵，该矩阵表示了每个单词在每个文档中的 TF-IDF 值。

在我们进行 fit_transform 拟合模型后，我们可以得到更多的 TF-IDF 向量属性，比如，我们可以得到词汇的对应关系（字典类型）和向量的 IDF 值，当然也可以获取设置的停用词 stop_words。

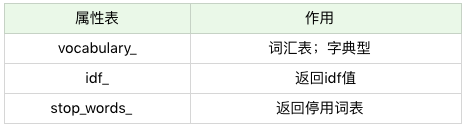
举个小例子吧：

假设我们有 4 个文档：

• 文档 1：this is the bayes document；
• 文档 2：this is the second second document；
• 文档 3：and the third one；
• 文档 4：is this the document。

现在想要计算文档里都有哪些单词，这些单词在不同文档中的 TF-IDF 值是多少呢？

1. 首先我们创建 TfidfVectorizer 类：

   from sklearn.feature_extraction.text import TfidfVectorizer
   tfidf_vec = TfidfVectorizer()
   

2. 然后我们创建 4 个文档的列表 documents，并让创建好的 tfidf_vec 对 documents 进行拟合，得到 TF-IDF 矩阵：

   documents = [
       'this is the bayes document',
       'this is the second second document',
       'and the third one',
       'is this the document'
   ]
   tfidf_matrix = tfidf_vec.fit_transform(documents)
   

   输出文档中所有不重复的词：

   print('不重复的词:', tfidf_vec.get_feature_names())
   
   # 结果如下：
   不重复的词: ['and', 'bayes', 'document', 'is', 'one', 'second', 'the', 'third', 'this']
   

   输出每个单词对应的 id 值：

   print('每个单词的ID:', tfidf_vec.vocabulary_)
   
   # 结果如下：
   每个单词的ID: {'this': 8, 'is': 3, 'the': 6, 'bayes': 1, 'document': 2, 'second': 5, 'and': 0, 'third': 7, 'one': 4}
   

   输出每个单词在每个文档中的 TF-IDF 值，向量里的顺序是按照词语的 id 顺序来的：

   print('每个单词的tfidf值:', tfidf_matrix.toarray())
   
   # 结果如下：
   
   每个单词的tfidf值: [[0.         0.63314609 0.40412895 0.40412895 0.         0.
     0.33040189 0.         0.40412895]
    [0.         0.         0.27230147 0.27230147 0.         0.85322574
     0.22262429 0.         0.27230147]
    [0.55280532 0.         0.         0.         0.55280532 0.
     0.28847675 0.55280532 0.        ]
    [0.         0.         0.52210862 0.52210862 0.         0.
     0.42685801 0.         0.52210862]]
   

5.3 如何对文档进行分类 - 思路分析

如果我们要对文档进行分类，有两个重要的阶段：

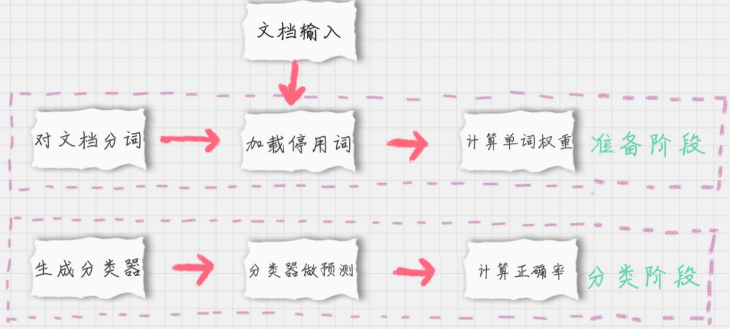
1. 基于分词的数据准备，包括分词、单词权重计算、去掉停用词；
2. 应用朴素贝叶斯分类进行分类，首先通过训练集得到朴素贝叶斯分类器，然后将分类器应用于测试集，并与实际结果做对比，最终得到测试集的分类准确率。

下面，分别对这些模块介绍:

• 模块 1：对文档进行分词
  在准备阶段里，最重要的就是分词。那么如果给文档进行分词呢？英文文档和中文文档所使用的分词工具不同。

  在英文文档中，最常用的是 NTLK 包。NTLK 包中包含了英文的停用词 stop words、分词和标注方法。

  import nltk
  word_list = nltk.word_tokenize(text) #分词
  nltk.pos_tag(word_list) #标注单词的词性
  

  在中文文档中，最常用的是 jieba 包。jieba 包中包含了中文的停用词 stop words 和分词方法。

  import jieba
  word_list = jieba.cut (text) #中文分词
  

• 模块 2：加载停用词表
  我们需要自己读取停用词表文件，从网上可以找到中文常用的停用词保存在 stop_words.txt，然后利用 Python 的文件读取函数读取文件，保存在 stop_words 数组中。

  stop_words = [line.strip().decode('utf-8') for line in io.open('stop_words.txt').readlines()]
  

• 模块 3：计算单词的权重
  直接创建 TfidfVectorizer 类，然后使用 fit_transform 方法进行拟合，得到 TF-IDF 特征空间 features，你可以理解为选出来的分词就是特征。我们计算这些特征在文档上的特征向量，得到特征空间 features。

  tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5)
  features = tf.fit_transform(train_contents)
  

  这里 max_df 参数用来描述单词在文档中的最高出现率。假设 max_df=0.5，代表一个单词在 50% 的文档中都出现过了，那么它只携带了非常少的信息，因此就不作为分词统计。一般很少设置 min_df，因为 min_df 通常都会很小。

• 模块 4：生成朴素贝叶斯分类器
  我们将特征训练集的特征空间 train_features，以及训练集对应的分类 train_labels 传递给贝叶斯分类器 clf，它会自动生成一个符合特征空间和对应分类的分类器。

  这里我们采用的是多项式贝叶斯分类器，其中 alpha 为平滑参数。为什么要使用平滑呢？因为如果一个单词在训练样本中没有出现，这个单词的概率就会被计算为 0。但训练集样本只是整体的抽样情况，我们不能因为一个事件没有观察到，就认为整个事件的概率为 0。为了解决这个问题，我们需要做平滑处理。

  当 alpha=1 时，使用的是 Laplace 平滑。Laplace 平滑就是采用加 1 的方式，来统计没有出现过的单词的概率。这样当训练样本很大的时候，加 1 得到的概率变化可以忽略不计，也同时避免了零概率的问题。

  当 0<alpha<1 时，使用的是 Lidstone 平滑。对于 Lidstone 平滑来说，alpha 越小，迭代次数越多，精度越高。我们可以设置 alpha 为 0.001。

  # 多项式贝叶斯分类器
  from sklearn.naive_bayes import MultinomialNB  
  clf = MultinomialNB(alpha=0.001).fit(train_features, train_labels)
  

• 模块 5：使用生成的分类器做预测
  首先我们需要得到测试集的特征矩阵。方法是用训练集的分词创建一个 TfidfVectorizer 类，使用同样的 stop_words 和 max_df，然后用这个 TfidfVectorizer 类对测试集的内容进行 fit_transform 拟合，得到测试集的特征矩阵 test_features。

  test_tf = TfidfVectorizer(stop_words=stop_words, max_df=0.5, vocabulary=train_vocabulary)
  test_features=test_tf.fit_transform(test_contents)
  

  然后我们用训练好的分类器对新数据做预测。方法是使用 predict 函数，传入测试集的特征矩阵 test_features，得到分类结果 predicted_labels。

  predict 函数做的工作就是求解所有后验概率并找出最大的那个。

• 模块 6：计算准确率
  计算准确率实际上是对分类模型的评估。我们可以调用 sklearn 中的 metrics 包，在 metrics 中提供了 accuracy_score 函数，方便我们对实际结果和预测的结果做对比，给出模型的准确率。

  from sklearn import metrics
  print metrics.accuracy_score(test_labels, predicted_labels)
  

5.4 实战文本分类

中文文档数据集点击这里下载。

数据说明：

文档共有 4 种类型：女性、体育、文学、校园；

训练集放到 train 文件夹里，测试集放到 test 文件，停用词放到 stop 文件夹里。

使用朴素贝叶斯分类对训练集进行训练，并对测试集进行验证，并给出测试集的准确率。

好吧，一步步的根据前面的思路进行做：

1. 导入包

   import os
   
   import jieba
   from sklearn.feature_extraction.text import TfidfVectorizer
   from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB
   from sklearn.metrics import accuracy_score
   

2. 加载停用词

   LABAL_MAP = {'体育':0, '女性':1, '文学':2, '校园':3}
   
   """加载停用词"""
   with open('./text classification/stop/stopword.txt', 'rb') as f:
       STOP_WORDS = [line.strip() for line in f.readlines()]
   

3. 加载数据集

   """定义加载数据的函数"""
   def load_data(path):
       """
           base_path: 基础路径
           return: 分词列表，标签列表
       """
       
       documents = []
       labels = []
   
       for label_dir in os.listdir(path):   # 这是遍历那四个标签目录
           file_path = os.path.join(path, label_dir)     
           for file in os.listdir(file_path):  # 这是遍历每个标签目录下面的文本
               labels.append(LABAL_MAP[label_dir])
               filename = os.path.join(file_path, file)
               with open(filename, 'rb') as fr:    # 读取文件  用二进制的方式读取，不用考虑字符编码问题
                   content = fr.read()
                   word_list = list(jieba.cut(content))
                   words = [wl for wl in word_list if wl not in STOP_WORDS]
                   documents.append(' '.join(words))
       
       return documents, labels
   

   """加载数据"""
   train_x, train_y = load_data('./text classification/train')
   test_x, text_y = load_data('./text classification/test')
   

4. 计算词的权重

   """计算TF-IDF矩阵"""
   tfidf_vec = TfidfVectorizer(stop_words=STOP_WORDS, max_df=0.5)
   new_train_x = tfidf_vec.fit_transform(train_x)
   
   # 测试集用训练集的词典
   test_tfidf_vec = TfidfVectorizer(stop_words=STOP_WORDS, max_df=0.5, vocabulary=tfidf_vec.vocabulary_)
   new_test_x = test_tfidf_vec.fit_transform(test_x)
   

5. 建立模型并预测（这里我对比了三种贝叶斯方式）

   """建立模型"""
   bayes_model = {}
   
   bayes_model['MultinomialNB'] = MultinomialNB(alpha=0.001)
   bayes_model['BernoulliNB'] = BernoulliNB(alpha=0.001)
   bayes_model['GaussianNB'] = GaussianNB()
   
   for item in bayes_model.keys():
       clf = bayes_model[item]
       clf.fit(new_train_x.toarray(), train_y)
       pred = clf.predict(new_test_x.toarray())
       print(item, "accuracy_score: ", accuracy_score(text_y, pred))
   

最后结果如下：

MultinomialNB accuracy_score:  0.91
BernoulliNB accuracy_score:  0.9
GaussianNB accuracy_score:  0.89

6. 总结

到这终于写完了， 我的天啊，没想到这个这么多，赶紧来总结一下吧，今天我们从贝叶斯原理出发，通过生活中的例子得出了伟大的贝叶斯公式，贝叶斯原理就是基于这个求后验概率。

然后又介绍了朴素贝叶斯及朴素之处，用两个案例解释了一下朴素贝叶斯的计算流程

然后，进行文本分类的实战，实战之前，介绍了文本处理时的一些知识，比如分词，比如TF-IDF统计方法原理及实现， 然后完成实战任务。

希望通过今天的学习能够掌握朴素贝叶斯的用法和原理。

参考：

• 极客时间数据分析实战45讲(上面网格图片的出处和实践项目都是摘自于此)
• 统计学习方法之朴素贝叶斯
• 朴素贝叶斯实战
• 通俗易懂讲解贝叶斯
• 数据分析实战45讲贝叶斯笔记
• 条件概率，全概率，贝叶斯公式理解
• 朴素贝叶斯的三个常用模型：高斯、多项式、伯努利

什么，还没看够？ 哈哈，可以看看其他的系列，也同样有趣又能学习到知识

• 白话机器学习算法理论+实战之决策树 - 帮你搞定相亲选择的烦恼
• 白话机器学习算法理论+实战之关联规则 - 带你领略导演拍戏一般会喜欢哪些演员的
• 白话机器学习算法理论+实战之PageRank算法 - 帮你分析与你对象交往的人员之间的关系紧密程度
• 白话机器学习算法理论+实战之AdaBoost算法 - 带你实现三个臭皮匠顶个诸葛亮的故事
• 白话机器学习算法理论+实战之支持向量机（SVM） - 教你检测是否有乳腺癌
• 白话机器学习算法理论+实战之K近邻算法 - 教你识别手写数字
• 白话机器学习算法理论+实战之KMearns聚类算法 - 帮你进行图像分割
• 白话机器学习算法理论+实战之EM聚类 - 带你走进王者荣耀英雄的聚类
• 白话机器学习算法理论+实战之PCA降维 - 带你玩一下人脸识别的降维

关于朴素贝叶斯， 高频面试题
朴素贝叶斯与LR的区别
朴素贝叶斯是生成模型，根据已有样本进行贝叶斯估计学习出先验概率$P(Y)$和条件概率$P(X|Y)$，进而求出联合分布概率$P(X,Y)$,最后利用贝叶斯定理求解$P(Y|X)$， 而LR是判别模型，根据极大化对数似然函数直接求出条件概率$P(Y|X)$；朴素贝叶斯是基于很强的条件独立假设（在已知分类$Y$的条件下，各个特征变量取值是相互独立的），而LR则对此没有要求；朴素贝叶斯适用于数据集少的情景，而LR适用于大规模数据集。

朴素贝叶斯“朴素”在哪里？
简单来说：利用贝叶斯定理求解联合概率$P(X,Y)$时，需要计算条件概率$P(X|Y)$。在计算$P(X|Y)$时，朴素贝叶斯做了一个很强的条件独立假设（当$Y$确定时，$X$的各个分量取值之间相互独立），即
$$P(X1=x1,X2=x2,...Xj=xj|Y=yk)=P(X1=x1|Y=yk)\ast P(X2=x2|Y=yk)\ast ...\ast P(Xj=xj|Y=yk)$$

朴素贝叶斯的优缺点

• 优点：对小规模的数据表现很好，适合多分类任务，适合增量式训练。
• 缺点：对输入数据的表达形式很敏感（离散、连续，值极大极小之类的），独立性假设一般不太可能满足。

最后

以上就是平淡枫叶为你收集整理的白话机器学习算法理论+实战之朴素贝叶斯的全部内容，希望文章能够帮你解决白话机器学习算法理论+实战之朴素贝叶斯所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。