【线性代数及其应用】04 -线性变换线性变换

线性变换

1. 矩阵与向量相乘的两重含义

1.1 重新线性组合

  对于矩阵与向量的乘法AX=b而言，从矩阵角度考虑，向量X的系数作为权值，让矩阵A中的各个列向量进行叠加，最后得到了一个重新线性组合的向量b

1.2 线性变换

  从向量角度来考虑，矩阵A对向量具有变换作用，通过矩阵A能够实现向量X的放缩、旋转、镜像等变换，这是矩阵乘法的线性变换含义。

2. 线性变换的分类

• 剪切变换

  剪切变换就是通过矩阵使得图形沿着某个方向滑动，一般是所有向量都加上了其中某一个向量的倍数，也就向着这个方向进行滑动

• 旋转变换

  旋转变换就是绕着原点顺时针或者逆时针转动一定角度

• 伸缩变换

  伸缩变换是所有向量整体增大或者减少一定倍数

• 镜像变换

  沿着某条轴做镜像对称得到新向量

3. 线性变换矩阵的求解

  线性变换满足数乘和加法的封闭，也就是
$$T(cX)=c\ast T(X)$$

$$T(X+Y)=T(X)+T(Y)$$

$$T(C1\ast X+C2\ast Y)=C1\ast T(X)+C2\ast T(Y)$$
  所以，我们只要知道基向量的变换情况，就可以通过基向量的组合得到任意向量的线性变换。比如
$$v=c_1\ast v_1+c_2\ast v_2+c_3\ast v_3$$

$$T(v)=c_1\ast T(v_1)+c_2\ast T(v_2)+c_3\ast T(v_3)$$

  我们以旋转为例进行说明

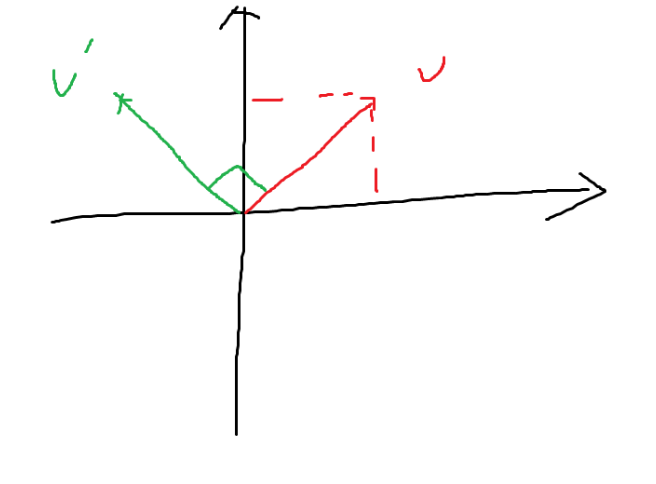
  假设向量旋转了90°，那么基向量必然也旋转了90°

  开始时候的基向量为
$$v1=\left\{\begin{array}{c}1\\ 0\end{array}\right\}$$

$$v2=\left\{\begin{array}{c}0\\ 1\end{array}\right\}$$
  而旋转之后的基向量为

$$v{1}^{\prime }=\left\{\begin{array}{c}0\\ 1\end{array}\right\}$$

$$v{2}^{\prime }=\left\{\begin{array}{c}-1\\ 0\end{array}\right\}$$

  所以变换矩阵为
$$A=\left\{\begin{array}{cc}0& -1\\ 1& 0\end{array}\right\}$$
  线性变换的操作为
$$v^{\prime }=A\ast v$$

4. 满射与单射

• 满射就是，通过现有的向量组合得到目标线性变换所需要的向量，至少有一种实现方式。相当于AX=b有1个或无穷多个解
• 单射就是，通过现有的向量组合得到目标线性变换所需要的向量，最多有一种实现方式。相当于AX=b有0或1个解

5. 线性变换与计算机图形学

5.1 旋转、伸缩、剪切变换

• 剪切变换矩阵

  水平剪切
$$\left\{\begin{array}{cc}1& m\\ 0& 1\end{array}\right\}$$

  垂直剪切
$$\left\{\begin{array}{cc}1& 0\\ m& 1\end{array}\right\}$$

• 伸缩变换
  $$\left\{\begin{array}{cc}m& 0\\ 0& 1\end{array}\right\}$$
  $$\left\{\begin{array}{cc}1& 0\\ 0& m\end{array}\right\}$$
• 旋转变换

$$\left\{\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right\}$$

• 复合变换
  $$A_1\ast A_2\ast .....\ast A_n$$

5.2 平移变换

5.2.1 齐次坐标系

  平移变换并不属于线性变换，因此，如果想要实现n维度空间的平移，必须构建n+1维度的空间，才能实现平移的线性变换，构造的n+1维度空间叫做齐次坐标系

5.2.2 二维的平移变换

  假设对v1实行平移变换
$$v1=\left\{\begin{array}{c}x\\ y\end{array}\right\}$$
  增加一个维度，让R²中的每个点(x,y)，都变成对应的(x,y,1)，放到R³中去，xy平面的上面一个单位上去。
$$w1=\left\{\begin{array}{c}x\\ y\\ 1\end{array}\right\}$$
  让(x,y)->(x+h,y+w)的变换可以写做

$$\left\{\begin{array}{ccc}1& 0& w\\ 0& 1& h\\ 0& 0& 1\end{array}\right\}\ast \left\{\begin{array}{c}x\\ y\\ 1\end{array}\right\}=\left\{\begin{array}{c}x+w\\ y+h\\ 1\end{array}\right\}$$

5.2.3 三维的平移变换

  三维平移变换也类似，构建四维齐次坐标系进行
$$\left\{\begin{array}{cccc}1& 0& 0& w\\ 0& 1& 0& h\\ 0& 0& 1& s\\ 0& 0& 0& 1\end{array}\right\}\ast \left\{\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right\}=\left\{\begin{array}{c}x+w\\ y+h\\ z+s\\ 1\end{array}\right\}$$
  一般来说(x,y,z,1)是(x,y,z)对应的齐次坐标，若最后一个数字不为1，应该通过除法使其变成1
$$(X,Y,Z,H)$$

$$x=\frac{X}{H}$$

$$y=\frac{Y}{H}$$

$$z=\frac{Z}{H}$$

5.3 透视投影

  透视投影就是，假设某个点(x,y,z),某个点望去，投影到某个平面上的时候，获得了投影点坐标。比如点(x,y,z),从(0,0,d)位置望去，投影在xy平面上的点是多少
  根据三角形相似关系，可以得到

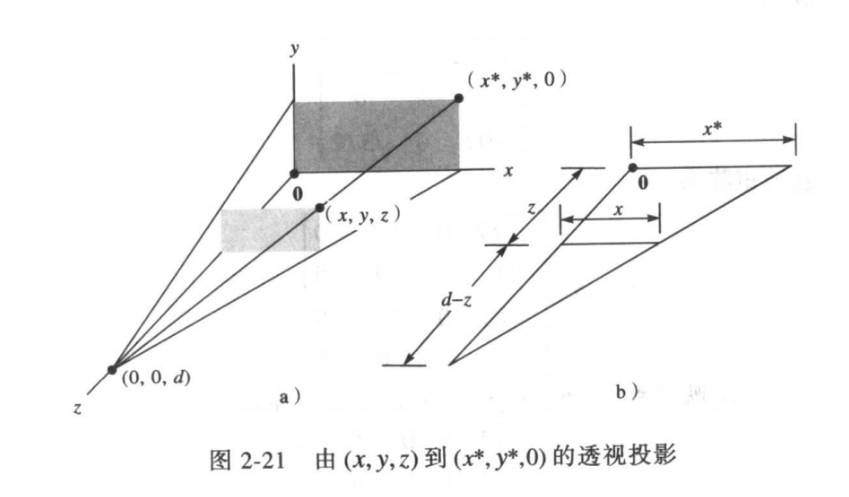
$$\frac{x}{x^{\prime }}=\frac{d-z}{d}$$
  可得x和y的投影坐标为
$$x^{\prime }=\frac{x}{1-z/d}$$

$$y^{\prime }=\frac{y}{1-z/d}$$

  所以(x,y,z,1)投影结果为(x’,y’,0,1)，让向量乘以1-z/d,变成(x,y,0,1-z/d)
$$\left\{\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 0\\ 0& 0& -\frac{1}{d}& 1\end{array}\right\}\ast \left\{\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right\}=\left\{\begin{array}{c}x\\ y\\ 0\\ 1-z/d\end{array}\right\}$$
  在齐次坐标系中，把最后一个坐标除为1，就得到了在三维空间中的透视投影点坐标了。

5.4 绕某点旋转

  假设有一个图形，想要绕着点p进行旋转一定角度，具体步骤为

• 图形平移-p到原点
• 绕原点进行旋转
• 旋转后的图形平移p到原位置

最后

以上就是羞涩铅笔为你收集整理的【线性代数及其应用】04 -线性变换线性变换的全部内容，希望文章能够帮你解决【线性代数及其应用】04 -线性变换线性变换所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。