深度剖析数据在内存中的存储（C语言）

深度剖析数据在内存中的存储（C语言）

1、对于整型来说：数据存放在内存中其实是存放的是补码
那么如何计算出一个整数的补码呢？
计算机有这样一个规定：对于一个有符号的整型来说，正数的原码、反码、补码相同。负数的原码、反码、补码不同，那么我们因如何计算一个整数的原码、反码、补码呢？
原码：直接将二进制按照正负数的形式翻译成二进制。
反码：将原码的符号位不变，其他位依次按位取反即可。
补码：反码+1得到补码。
对于整型在内存中，其实存放的是它的补码。
列如：

因为补码在内存中是以十六进制存储的，所以我们需将二进制的补码翻译成十六进制形式。
但看到这里，不知道你是否有疑惑，为什么a在内存中是倒着存的？正常人的思维都会认为a在内存中是00000009这样存储的。这又是什么原因导致的呢？
导致这个结果的原因是因为计算机在存储整型数据是存在两种存储形式，一个是大端存储形式，一个是小端存储形式。那么何为大端，小段？
大端：是指数据的地位保存在内存的高地址中，而数据的高位，保存在低地址中。
小端：是指数据的地位保存在内存的低地址中，而数据的高位，保存在内存的高地址中。

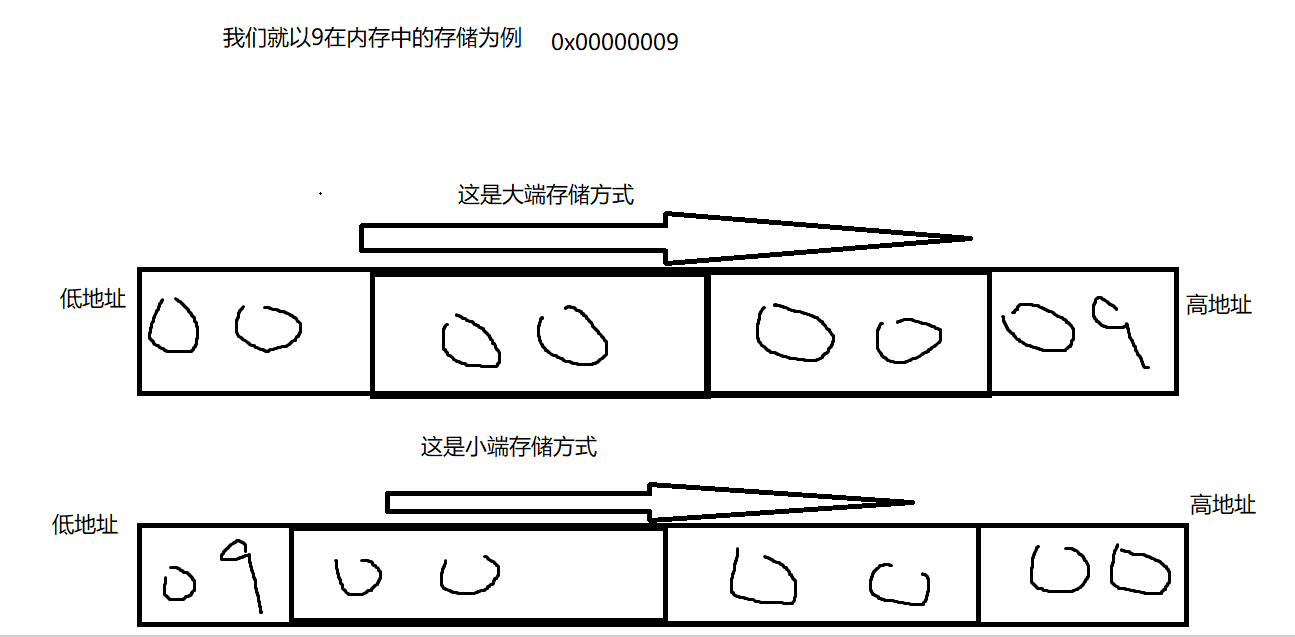
想必看到这里，读者应该对整型在内存中的存储应该不陌生了，下面我们就来介绍浮点型在内存中的存储
根据国家标准IEEE754规定，任意一个二进制浮点数V可以表示为以下形式
(-1)^S*M*2E
(-1)^S表示符号位，当s=0,V为正数；当s=1时，V为负数
M表示有效数字，大于等于1，小于2.
2^E表示指数位。

但是我们对于浮点数的小数点后面的数在内存中的存储总是不能非常精确，因此计算机为了提高精度，对于M我们有这样的规定，由于1<=M<2,因此我们将小数点前面的1省略掉，等拿出来的时候加上1即可，从此有提升了一个精度


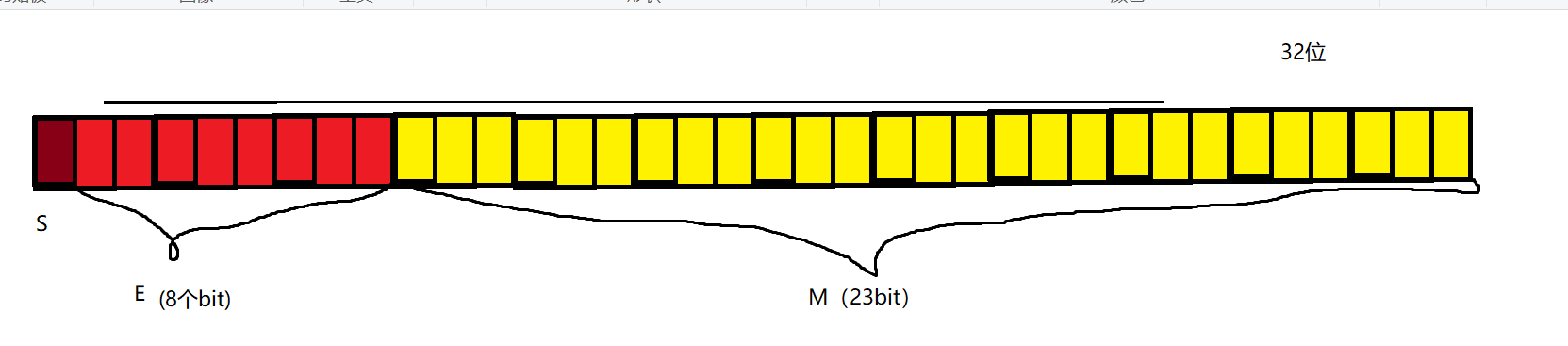
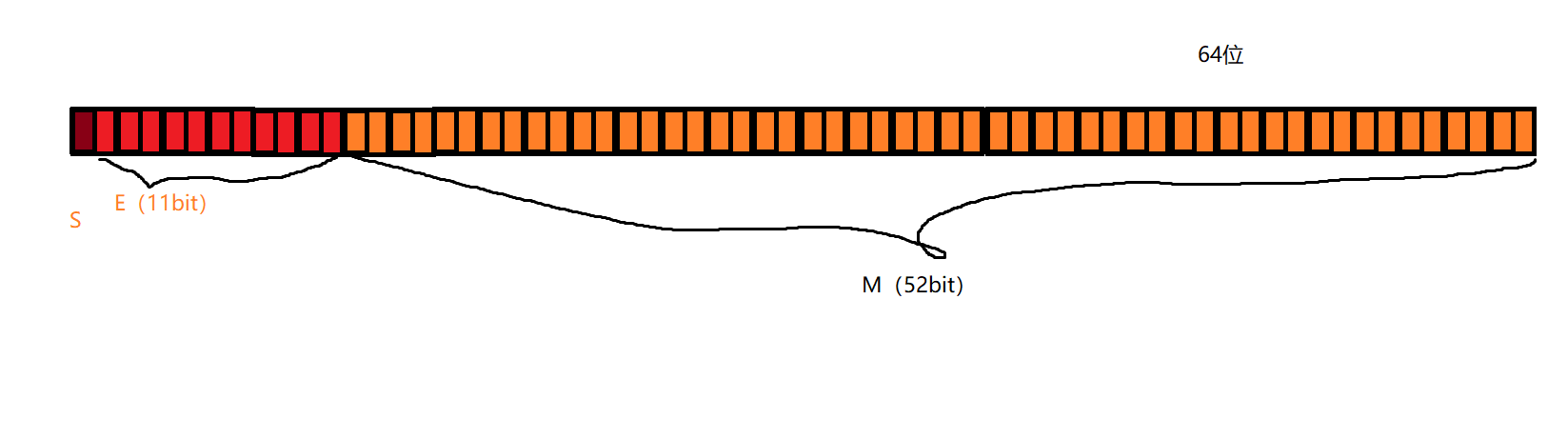
至于指数E是如何放入内存中去的
首先,E为一个无符号整数，因为在科学计数法中E可以出现负数，所以IEEE754规定，存入内存是E的真实值必须加上一个中间数，对于8位的E，这个中间数是127，对于11位的E，这个中间数是1023，比如2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001.
然而，指数E从内存中取出还可以再分成三种情况：
(1)E不全为0或者不全为1：这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将有效数字M前 加上第一位的1。比如：0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为1.0*2^(-1)，其阶码为-1+127=126，表示为01111110，而尾数1.0去掉整数部分为0，补齐0到23位
00000000000000000000000，则其二进制表示形式为:
（2）E全为0：这时，浮点数的指数E等于1-127（或者1-1023）即为真实值，有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于0的很小的数字。
（3）E全为1：这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）
下面我们就以一道题目为例



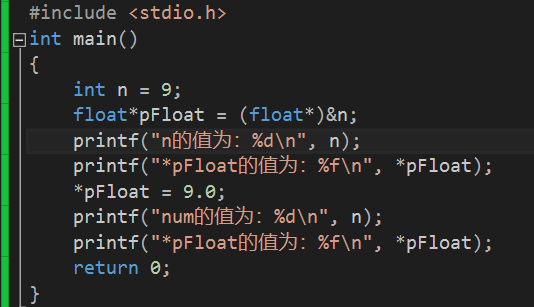
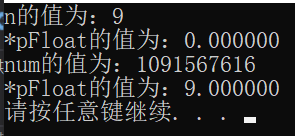
这就关于整型与浮点型在内存中存储的全部内容。

最后

以上就是直率烤鸡为你收集整理的深度剖析数据在内存中的存储（C语言）的全部内容，希望文章能够帮你解决深度剖析数据在内存中的存储（C语言）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。