Tensorflow入门——利用神经网络实现线性回归的预测

之前讲到了基于tensorflow解决线性回归的预测问题：Tensorflow——实现最简单的线性回归模型的预测(原)

其中，我们是在已知直线方程 y = w * x + b的前提下，通过机器学习来反推出w和b的值

但是如果在没有已知方程的前提下，如何来根据给定的x值预测y的值呢？那么这时候就需要用到（多层）神经网络了

====================================================

我们将之前的代码改成神经网络的实现，只需要将模型部分修改一下就可以了

W = tf.Variable(tf.zeros([1]))
B = tf.Variable(tf.zeros([1]))
OUT = X * W + B

把这部分模型改成（多层）神经网络

下面一共有三层，L1和L2是神经网络层（隐藏层），OUT为输出层L1有10个神经元，L2有10个神经元，OUT只有一个输出（就是y的预测值）

W1 = tf.Variable(tf.random_normal([1, 10]))
B1 = tf.Variable(tf.random_normal([10]))
L1 = tf.nn.relu(tf.add(tf.matmul(X, W1), B1))

W2 = tf.Variable(tf.random_normal([10, 10]))
B2 = tf.Variable(tf.random_normal([10]))
L2 = tf.nn.relu(tf.add(tf.matmul(L1, W2), B2))

WOUT = tf.Variable(tf.random_normal([10, 1]))
BOUT = tf.Variable(tf.random_normal([1]))
OUT = tf.nn.relu(tf.add(tf.matmul(L2, WOUT), BOUT))

至于W1为什么是1*10，W2为什么是10*10，WOUT为什么是10*1

在神经网络中的意义：

• 输入层1个节点连接到L1层的10个节点
• L1层的10个节点连接到L2层的10个节点
• L2层的10个节点连接到输出层的1个节点

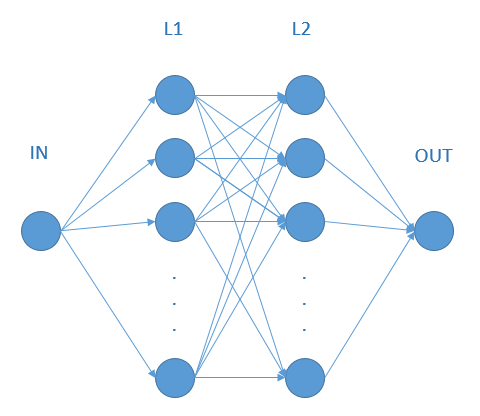
在矩阵运算中的意义：

• input的1*1和L1的1*10矩阵相乘得到一个1*10的矩阵
• 再和L2的10*10矩阵相乘，仍然是一个1*10的矩阵
• 最后和输出层的10*1矩阵相乘，得到一个1*1的矩阵，就是output

参数B（B1、B2、BOUT）为偏移量，长度和当层神经元的个数相同

====================================================

但是仅仅做这些修改是无法正常运行的，会有运行时异常，因为神经网络的运算是矩阵运算，所以我们需要将相关的地方都改成矩阵

占位改成1*1的矩阵

X = tf.placeholder(tf.float32, [1, 1])
Y = tf.placeholder(tf.float32, [1, 1])

训练和预测的部分输入值也必须是1*1矩阵

sess.run([optimizer, loss], feed_dict={X: [[x_data]], Y: [[y_data]]})

sess.run(OUT, feed_dict={X: [[x_data]]})

损失函数仍然使用之前的方差函数，为了将训练速度加快，我们将训练步长改为0.01

loss = tf.reduce_mean(tf.square(Y - OUT))
optimizer = tf.train.AdamOptimizer(0.01).minimize(loss)

训练过程如下：

因为没有使用直线方程作为模型，不存在变量w和b，所以这边就没有打印w和b的值

epoch= 0 _loss= 2499.2158
epoch= 5000 _loss= 26.200289
epoch= 10000 _loss= 18.451694
epoch= 15000 _loss= 27.851042
epoch= 20000 _loss= 0.80013156
epoch= 25000 _loss= 6.399736
epoch= 30000 _loss= 0.42621955
epoch= 35000 _loss= 6.539572
epoch= 40000 _loss= 118.756004
epoch= 45000 _loss= 9.849824

预测结果如下：

从中可以发现第3次的预测结果相差很大，其他的预测结果还是很接近的

x= 6.701938926943123 y预测= [[13.210411]] y实际= 12.461334480606848
x= 14.517219202811821 y预测= [[55.388046]] y实际= 54.116778350987005
x= 0.5071548382130286 y预测= [[-0.]] y实际= -20.556864712324558
x= 4.522887130946821 y预测= [[1.7613227]] y实际= 0.8469884079465544
x= 15.859426349977381 y预测= [[62.63169]] y实际= 61.27074244537944
x= 20.760960906047075 y预测= [[89.08439]] y实际= 87.3959216292309
x= 27.817233959488124 y预测= [[127.16579]] y实际= 125.0058570040717
x= 7.207120423200983 y预测= [[15.936781]] y实际= 15.153951855661237
x= 18.68547195335005 y预测= [[77.88335]] y实际= 76.33356551135576
x= 6.211735333477534 y预测= [[10.56487]] y实际= 9.848549327435254

====================================================

由于神经网络的不确定性，哪怕是相同的模型和相同的样本，每次的训练结果也会不一样

这里是因为选用的损失函数可能有点问题，不是每次训练都会成功

另外，如果预测结果精度不够，可以通过增加训练的方法来提高精度，就是使用更多的样本来进行训练

epoch= 0 _loss= 2526.3677
epoch= 5000 _loss= 4273.6484
epoch= 10000 _loss= 10332.345
epoch= 15000 _loss= 65.311
epoch= 20000 _loss= 9910.367
epoch= 25000 _loss= 5564.832
epoch= 30000 _loss= 10158.441
epoch= 35000 _loss= 249.78651
epoch= 40000 _loss= 4314.363
epoch= 45000 _loss= 702.9666

x= 12.38727016058595 y预测= [[-0.]] y实际= 42.764149955923116
x= 10.922809365164358 y预测= [[-0.]] y实际= 34.95857391632603
x= 9.296139279977996 y预测= [[-0.]] y实际= 26.28842236228272
x= 4.085033713695978 y预测= [[-0.]] y实际= -1.4867703060004374
x= 5.896742509909711 y预测= [[-0.]] y实际= 8.169637577818758
x= 12.12864019253157 y预测= [[-0.]] y实际= 41.38565222619326
x= 26.964092732084474 y预测= [[-0.]] y实际= 120.45861426201024
x= 0.8534877898439863 y预测= [[-0.]] y实际= -18.710910080131555
x= 4.472453183527925 y预测= [[-0.]] y实际= 0.5781754682038382
x= 26.249269554849263 y预测= [[-0.]] y实际= 116.64860672734657

====================================================

完整代码如下，在python3.6.8、tensorflow1.13环境下成功运行

https://github.com/yukiti2007/sample/blob/master/python/tensorflow/wx_b_nn.py

import random

import matplotlib.pyplot as plt
import tensorflow as tf


def create_data(for_train=False):
    w = 5.33
    b = -23.26
    x = random.random() * 30
    y = w * x + b

    if for_train:
        noise = (random.random() - 0.5) * 10
        y += noise

    return x, y


def draw():
    x_data, y_data = [], []
    for _ in range(100):
        x, y = create_data(True)
        x_data.append(x)
        y_data.append(y)
    plt.figure()
    plt.scatter(x_data, y_data)
    plt.show()


def run():
    LOSS = []
    STEP = []
    X = tf.placeholder(tf.float32, [1, 1])
    Y = tf.placeholder(tf.float32, [1, 1])

    W1 = tf.Variable(tf.random_normal([1, 10]))
    B1 = tf.Variable(tf.random_normal([10]))
    L1 = tf.nn.relu(tf.add(tf.matmul(X, W1), B1))

    W2 = tf.Variable(tf.random_normal([10, 10]))
    B2 = tf.Variable(tf.random_normal([10]))
    L2 = tf.nn.relu(tf.add(tf.matmul(L1, W2), B2))

    WOUT = tf.Variable(tf.random_normal([10, 1]))
    BOUT = tf.Variable(tf.random_normal([1]))
    OUT = tf.nn.relu(tf.add(tf.matmul(L2, WOUT), BOUT))

    loss = tf.reduce_mean(tf.square(Y - OUT))
    optimizer = tf.train.AdamOptimizer(0.01).minimize(loss)

    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        for epoch in range(50000):
            x_data, y_data = create_data(True)
            _, _loss = sess.run([optimizer, loss], feed_dict={X: [[x_data]], Y: [[y_data]]})
            if 0 == epoch % 500:
                LOSS.append(_loss)
                STEP.append(epoch)
            if 0 == epoch % 5000:
                print("epoch=", epoch, "_loss=", _loss)

        print("")

        for step in range(10):
            x_data, y_data = create_data(False)
            prediction_value = sess.run(OUT, feed_dict={X: [[x_data]]})
            print("x=", x_data, "y预测=", prediction_value, "y实际=", y_data)

    plt.figure()
    plt.scatter(STEP, LOSS)
    plt.show()


if __name__ == "__main__":
    # draw()
    run()