【TensorFlow 2】实现线性回归

62 阅读 0 评论 41 点赞

我是靠谱客的博主落后红酒，最近开发中收集的这篇文章主要介绍【TensorFlow 2】实现线性回归，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

低阶API

数据生成

import matplotlib.pyplot as plt
import tensorflow as tf
%matplotlib inline

TRUE_W = 3.0
TRUE_b = 2.0
NUM_SAMPLES = 100

# 初始化随机数据
X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()
y = X * TRUE_W + TRUE_b + noise  # 添加噪声

plt.scatter(X, y)

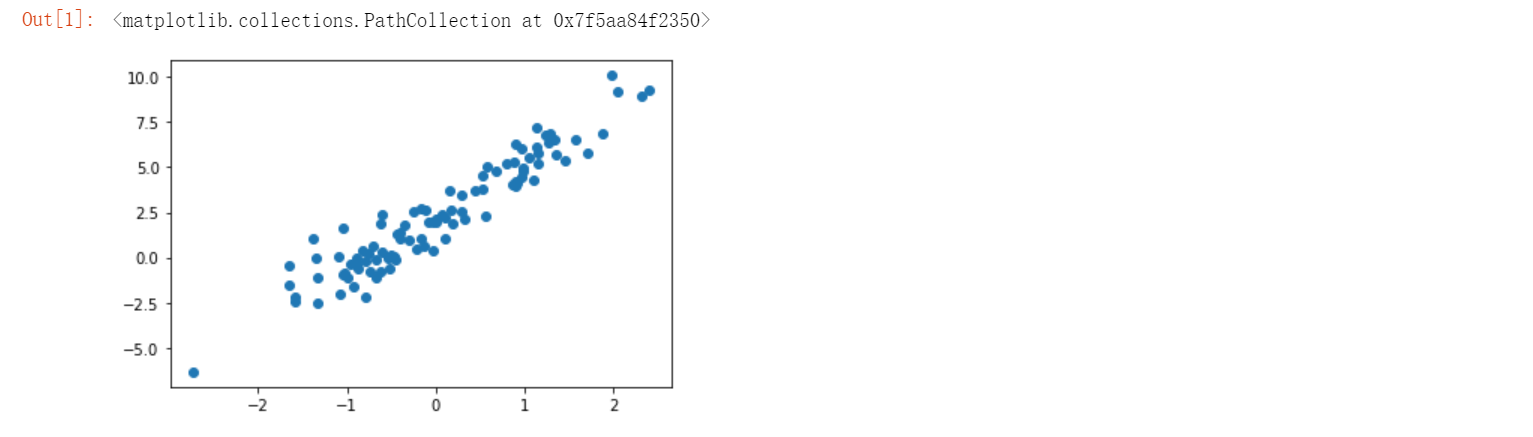
在这里插入图片描述

模型构建
这里我们构建自定义模型类,并使用 TensorFlow提供的tf.Variable随机初始化参数????和截距项????。

class Model(object):
    def __init__(self):
        self.W = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))

    def __call__(self, x):
        return self.W * x + self.b  # w*x + b

模型显示

model = Model()  # 实例化模型

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

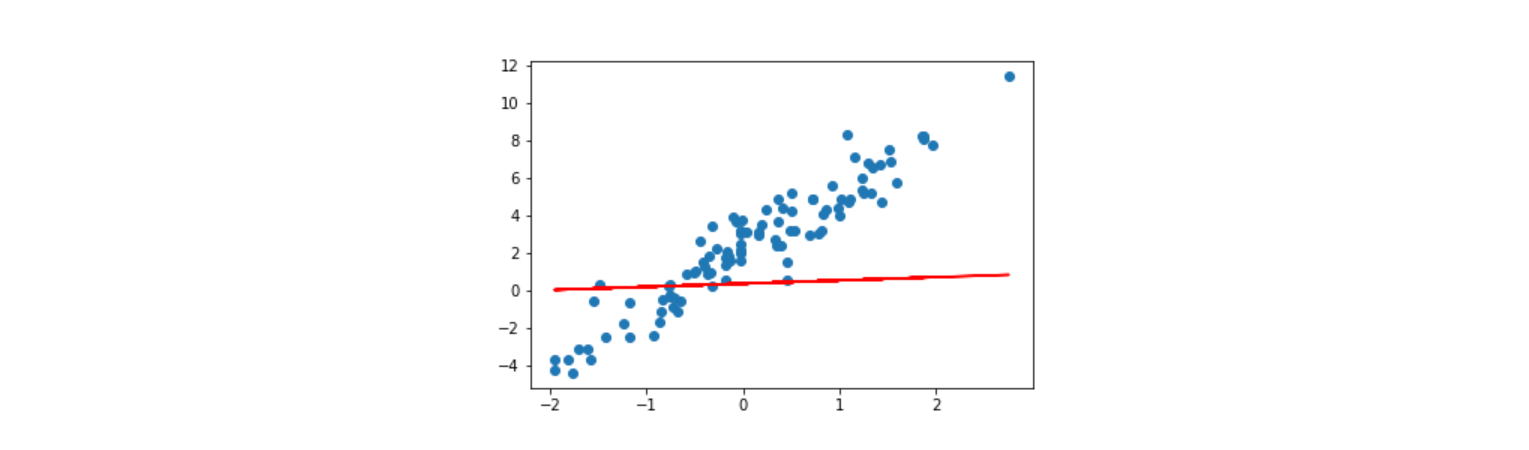
在这里插入图片描述

def loss_fn(model, x, y):
    y_ = model(x)
    return tf.reduce_mean(tf.square(y_ - y))

EPOCHS = 10  # 全部数据迭代 10 次
LEARNING_RATE = 0.1  # 学习率

for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X, y)  # 计算损失
    dW, db = tape.gradient(loss, [model.W, model.b])  # 计算梯度
    model.W.assign_sub(LEARNING_RATE * dW)  # 更新梯度
    model.b.assign_sub(LEARNING_RATE * db)
    # 输出计算过程
    print(f'Epoch [{epoch}/{EPOCHS}], loss [{loss}], W/b [{model.W.numpy()}/{model.b.numpy()}]')

'''
Epoch [0/10], loss [13.112443923950195], W/b [[0.62060654]/[0.7564423]]
Epoch [1/10], loss [8.532510757446289], W/b [[1.0952367]/[1.0635427]]
Epoch [2/10], loss [5.67167854309082], W/b [[1.470548]/[1.3059648]]
Epoch [3/10], loss [3.8846704959869385], W/b [[1.7673266]/[1.497326]]
Epoch [4/10], loss [2.7684197425842285], W/b [[2.0020072]/[1.6483777]]
Epoch [5/10], loss [2.0711536407470703], W/b [[2.1875854]/[1.7676079]]
Epoch [6/10], loss [1.6356059312820435], W/b [[2.334336]/[1.8617182]]
Epoch [7/10], loss [1.363539695739746], W/b [[2.4503841]/[1.935999]]
Epoch [8/10], loss [1.1935921907424927], W/b [[2.5421543]/[1.994627]]
Epoch [9/10], loss [1.0874332189559937], W/b [[2.614726]/[2.0408995]]
'''

上面的代码中，我们初始化 tf.GradientTape() 以追踪梯度然后使用 tape.gradient 方法就可以计算梯度了。值得注意的是，tape.gradient() 第二个参数支持以列表形式传入多个参数同时计算梯度。紧接着，使用 .assign_sub 即可完成公式中的减法操作用以更新梯度。

最终，我们绘制参数学习完成之后，模型的拟合结果。

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

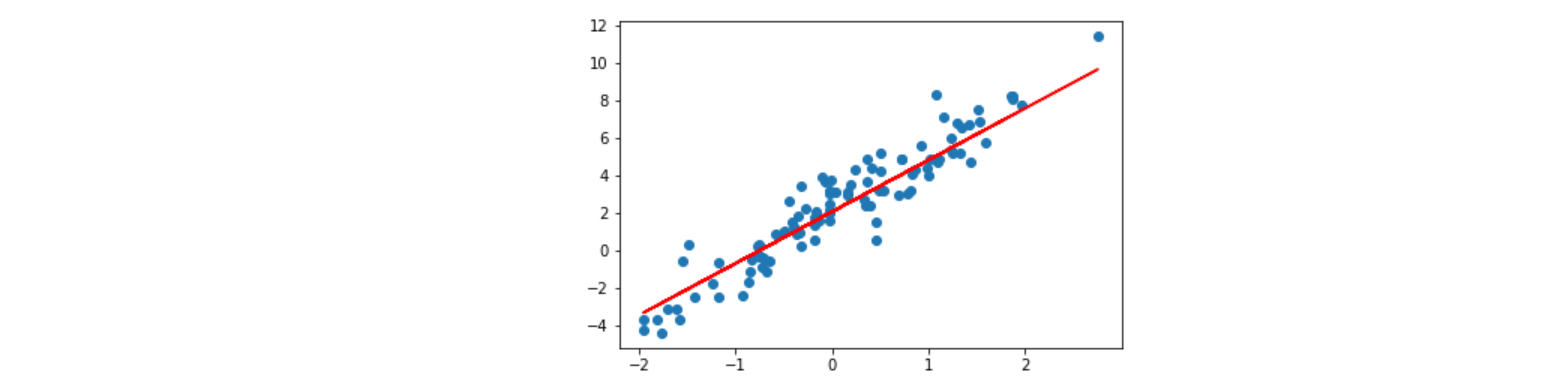
在这里插入图片描述
由于是随机初始化参数，如果迭代后拟合效果仍然不好，一般是迭代次数太少的原因。你可以重复执行上面的迭代单元格多次，增加参数更新迭代次数，即可改善拟合效果。此提示对后面的内容同样有效。

高阶 API 实现

TensorFlow 2 中提供了大量的高阶 API 帮助我们快速构建所需模型，接下来，我们使用一些新的 API 来完成线性回归模型的构建。这里还是沿用上面提供的示例数据。

tf.keras 模块下提供的 tf.keras.layers.Dense 全连接层（线性层）实际上就是一个线性计算过程。所以，模型的定义部分我们就可以直接实例化一个全连接层即可。

model = tf.keras.layers.Dense(units=1)  # 实例化线性层
model
plt.scatter(X, y)
plt.plot(X, model(X), c='r')

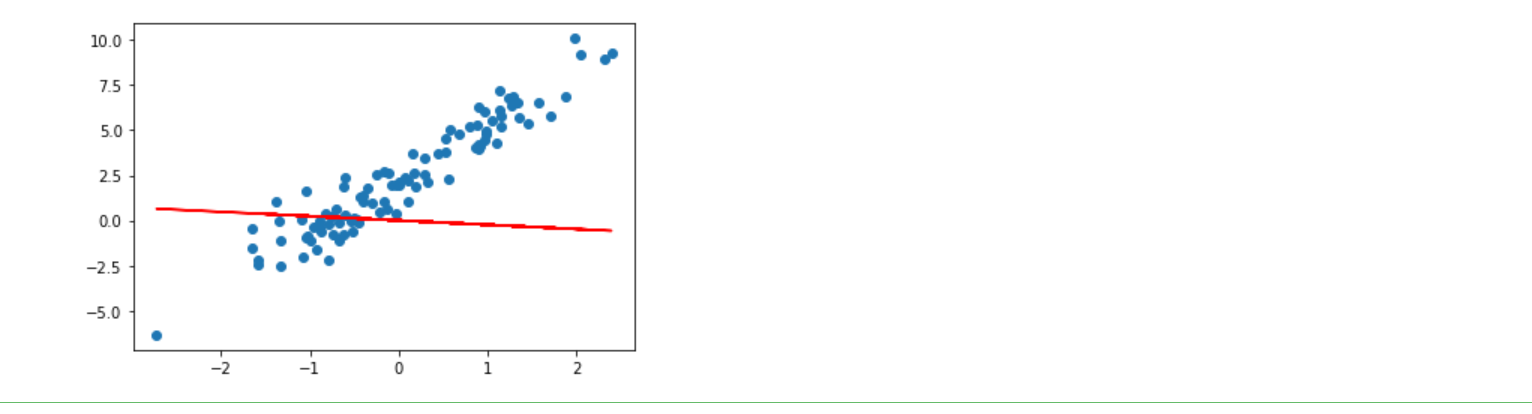
在这里插入图片描述
你可以使用 model.variables 打印出模型初始化的随机参数。

model.variables
'''
[<tf.Variable 'dense/kernel:0' shape=(1, 1) dtype=float32, numpy=array([[-0.23846269]], dtype=float32)>,
 <tf.Variable 'dense/bias:0' shape=(1,) dtype=float32, numpy=array([0.], dtype=float32)>]
'''

接下来就可以直接构建模型迭代过程了。

这里同样使用 tf.GradientTape() 来追踪梯度，我们简化损失计算和更新的过程。首先，损失函数无需再自行构造，我们可以直接使用 TensorFlow 提供的平方损失函数 tf.keras.losses.mean_squared_error 计算，然后使用 tf.reduce_sum 求得全部样本的平均损失。

EPOCHS = 10
LEARNING_RATE = 0.002
for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        y_ = model(X)
        loss = tf.reduce_sum(tf.keras.losses.mean_squared_error(y, y_))  # 计算损失

    grads = tape.gradient(loss, model.variables)  # 计算梯度
    optimizer = tf.keras.optimizers.SGD(LEARNING_RATE)  # 随机梯度下降
    optimizer.apply_gradients(zip(grads, model.variables))  # 更新梯度
    print(f'Epoch [{epoch}/{EPOCHS}], loss [{loss}]')
'''
Epoch [0/10], loss [1630.552490234375]
Epoch [1/10], loss [610.0955810546875]
Epoch [2/10], loss [266.05828857421875]
Epoch [3/10], loss [150.06939697265625]
Epoch [4/10], loss [110.96483612060547]
Epoch [5/10], loss [97.78109741210938]
Epoch [6/10], loss [93.33631896972656]
Epoch [7/10], loss [91.83782196044922]
Epoch [8/10], loss [91.33259582519531]
Epoch [9/10], loss [91.16226959228516]
'''

其次，使用 model.variables 即可读取可参数的列表，无需像上面那样手动传入参数。这里不再按公式手动更新梯度，而是使用现有的随机梯度下降函数 tf.keras.optimizers.SGD，然后使用 apply_gradients 即可更新梯度。

TensorFlow 中没有提供上方手动实现的梯度下降算法，只提供了随机梯度下降算法。随机梯度下降可以看成梯度下降的升级版本，具体区别大家可以自行搜索了解。

最终，同样将迭代完成的参数绘制拟合直线到原图中。

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

Keras 方式实现

配合 TensorFlow 提供的高阶 API，我们省去了定义线性函数，定义损失函数，以及定义优化算法等 3 个步骤。至此，你应该可以初步感受到 TensorFlow 的易用性和存在的必要性了。不过，上面的高阶 API 实现过程实际上还不够精简，我们可以完全使用 TensorFlow Keras API 来实现线性回归。
Keras 本来是一个用 Python 编写的独立高阶神经网络 API，它能够以 TensorFlow, CNTK，或者 Theano 作为后端运行。目前，TensorFlow 已经吸纳 Keras，并组成了 tf.keras 模块。官方介绍，tf.keras 和单独安装的 Keras 略有不同，但考虑到未来的发展趋势，实验以学习 tf.keras 为主。
我们这里使用 Keras 提供的 Sequential 顺序模型结构。和上面的例子相似，向其中添加一个线性层。不同的地方在于，Keras 顺序模型第一层为线性层时，规定需指定输入维度，这里为 input_dim=1。

model = tf.keras.Sequential()  # 新建顺序模型
model.add(tf.keras.layers.Dense(units=1, input_dim=1))  # 添加线性层
model.summary()  # 查看模型结构
'''
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 1)                 2         
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________
'''

接下来，直接使用 .compile 编译模型，指定损失函数为 MSE 平方损失函数，优化器选择 SGD 随机梯度下降。然后，就可以使用 .fit 传入数据开始迭代了。

model.compile(optimizer='sgd', loss='mse')  # 定义损失函数和优化方法
model.fit(X, y, epochs=10, batch_size=32)  # 训练模型
'''
Train on 100 samples
Epoch 1/10
100/100 [==============================] - 0s 4ms/sample - loss: 11.0354
Epoch 2/10
100/100 [==============================] - 0s 100us/sample - loss: 9.4507
Epoch 3/10
100/100 [==============================] - 0s 886us/sample - loss: 8.0920
Epoch 4/10
100/100 [==============================] - 0s 876us/sample - loss: 7.1554
Epoch 5/10
100/100 [==============================] - 0s 130us/sample - loss: 6.2682
Epoch 6/10
100/100 [==============================] - 0s 99us/sample - loss: 5.5206
Epoch 7/10
100/100 [==============================] - 0s 83us/sample - loss: 4.9169
Epoch 8/10
100/100 [==============================] - 0s 95us/sample - loss: 4.2957
Epoch 9/10
100/100 [==============================] - 0s 837us/sample - loss: 3.7687
Epoch 10/10
100/100 [==============================] - 0s 83us/sample - loss: 3.3058
<tensorflow.python.keras.callbacks.History at 0x7f5aa809e690>
'''

batch_size 是采用小批次训练的参数，主要用于解决一次性传入数据过多无法训练的问题。当然，由于示例数据本身较少，这里意义不大，但还是按照常规使用方法进行设置。

接下来，我们可以绘制最终的训练结果了。

plt.scatter(X, y)
plt.plot(X, model(X), c='r')

总结：完全使用 Keras 高阶 API 实际上只需要 4 行核心代码即可完成，相比于最开始的低阶 API 简化了很多。

model = tf.keras.Sequential()  # 新建顺序模型
model.add(tf.keras.layers.Dense(units=1, input_dim=1))  # 添加线性层
model.compile(optimizer='sgd', loss='mse')  # 定义损失函数和优化方法
model.fit(X, y, epochs=10, batch_size=32)  # 训练模型