线性回归tensorflow实现

线性回归tensorflow实现

xiaoyao 《动手学深度学习》 tensorflow2.1.0

import tensorflow as tf
print(tf.__version__)

# from Ipython import display
from matplotlib import pyplot as plt
import random
%matplotlib inline

import warnings
warnings.filterwarnings('ignore')

2.1.0

3.2.1 生成数据集

利用tensor和GradientTape实现一个线性回归的训练

设训练集样本数为1000， 特征数为2. 给定生成的批量样本特征$\mathbf{X}\in {\mathbb{R}}^{1000\times 2}$,使用线性回归模型真实权重为:$\mathbf{w}=[2,-3.4]$和偏差$b=4.2$，以及一个噪声项$ϵ$来生成标签：
$$\mathcal{Y}=\mathbf{X}\mathbf{w}+b+ϵ\text{\hspace{1em}(式1)}$$
其中噪声项$ϵ$服从均值为0，标准差为0.01的正态分布。噪声代表了数据集中无意义的干扰。

num_inputs = 2
num_examples = 1000

true_w = [2, -3.4]
true_b = 4.2

features = tf.random.normal((num_examples, num_inputs),stddev = 1)
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += tf.random.normal(labels.shape,stddev=0.01)

features[0], labels[0]

(<tf.Tensor: shape=(2,), dtype=float32, numpy=array([-1.1710224,  1.3963023], dtype=float32)>,
 <tf.Tensor: shape=(), dtype=float32, numpy=-2.8871787>)

这里，features的每一行是长度为2的向量，而labels的每一行是长度为1的向量（标量）

print(features[0], labels[0])

tf.Tensor([-1.1710224  1.3963023], shape=(2,), dtype=float32) tf.Tensor(-2.8871787, shape=(), dtype=float32)

"""
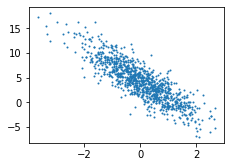
生成第二个特征features[:,1]和标签labels的散点图，这里可以更加直观的反映出
两者之间的线性关系
"""
def set_figsize(figsize=(3.5, 2.5)):
    plt.rcParams['figure.figsize'] = figsize

set_figsize()
plt.scatter(features[:, 1], labels, 1) # 0设置为透明，1设置为不透明

<matplotlib.collections.PathCollection at 0x246120031c8>

3.2.2 读取数据

在每次训练模型的时候，需要遍历数据集同时需要不断读取小批量数据样本。定义一个
函数，每次返回batch_size（批量大小）个随机样本的特征和标签。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        j = indices[i: min(i+batch_size, num_examples)]
        yield tf.gather(features, axis=0, indices=j), tf.gather(labels, axis=0, indices=j)

batch_size = 10

for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

tf.Tensor(
[[-1.6544346  -0.21689671]
 [-1.9006996  -0.60220146]
 [ 0.47630018  0.16197595]
 [ 0.6305033   0.06080767]
 [-0.38096488 -0.72073525]
 [-1.8225852   0.7859634 ]
 [ 2.5961044   2.010577  ]
 [ 0.23788874 -0.70898366]
 [ 1.5793388  -0.97015315]
 [-2.655049   -0.67389566]], shape=(10, 2), dtype=float32) tf.Tensor(
[ 1.6189524  2.4591262  4.5916023  5.2634425  5.903998  -2.1094294
  2.5460227  7.093977  10.664606   1.1736389], shape=(10,), dtype=float32)

3.2.3 初始化模型参数

将权重初始化为均值为零，标准差为0.01的正态分布随机数，偏差初始化为0

w = tf.Variable(tf.random.normal((num_inputs, 1), stddev=0.01))
b = tf.Variable(tf.zeros((1,)))

3.2.4 定义模型define model

# 利用矢量计算表达式实现，使用tf.matmul函数做矩阵乘法
def linreg(X, w, b):
    return tf.matmul(X, w) + b

3.2.5 定义损失函数define loss

# 这里需要将真实值y变形reshape成y_hat的形状。此函数返回的结果将和y_hat的形状
# 一致
def squared_loss(y_hat, y):
    return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 /2  
    # tf.reshape(tensor, shape, name=None) 函数说明

3.2.6 定义优化算法define optimization

"""
实现小批量梯度下降。通过不断迭代模型参数来优化损失函数，这里自动求梯度模块
计算得来的梯度是一个批量样本的梯度和，将其除以批量大小来得到平均值。
"""
def sgd(params, lr, batch_size, grads):
    """Mini-batch stochastic gradient descent."""
    for i, param in enumerate(params):
        param.assign_sub(lr * grads[i] / batch_size)

3.2.7 训练模型training

在每次迭代中，根据当前读取的小批量数据样本（特征x和标签y）,通过调用反向函数t.gradients计算小批量随机梯度，同时调用优化算法sgd迭代模型参数。由于之前设置的批量大小为batch_size为10，每个小批量的损失l的形状为（10， 1）。

由于变量l不是一个标量，所以这里调用reduce_sum()将其求和得到一个标量，再运行t.gradients得到该变量关于模型参数的梯度。每次更新完参数之后将参数的梯度清零。

在一个迭代周期（epoch）中，我们将完整遍历一遍data_iter函数，并对训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设3和0.03。在实践中，大多超参数都需要通过反复试错来不断调节。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        with tf.GradientTape() as t:
            t.watch([w,b])
            l = loss(net(X, w, b), y)
        grads = t.gradient(l, [w, b])
        sgd([w, b], lr, batch_size, grads)
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, tf.reduce_mean(train_l)))

epoch 1, loss 0.033065
epoch 2, loss 0.000111
epoch 3, loss 0.000050

# 训练完成之后，可以将学习到的参数和用来生成训练集的真实参数进行比较
true_w, w

([2, -3.4],
 <tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
 array([[ 2.000201 ],
        [-3.4001694]], dtype=float32)>)

true_b, b

(4.2,
 <tf.Variable 'Variable:0' shape=(1,) dtype=float32, numpy=array([4.199146], dtype=float32)>)

最后

以上就是美丽抽屉为你收集整理的线性回归tensorflow实现的全部内容，希望文章能够帮你解决线性回归tensorflow实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。