数据统计基础概念
- 误差(error)
- 偏差(Bias)
- 残差(residual)
- 方差(Variance)
误差(error)
观察值与真实值之间的差。我们任何一次测量都是有误差的,比如用一把米尺测量桌子的宽度,但是因为尺子的精度问题,导致并不能测出真实的宽度,再改用游标卡尺等等只能尽可能的缩小误差,但是无法避免误差。
经典测验理论(CTT)的基本假设是:X=T+E。观察值等于真实值加上误差,误差由于是随机分布且均值为0,所以可以用多次测量的观测值作为真实值。
偏差(Bias)
用误差衡量测量结果的准确度,用偏差衡量测量结果的精密度;误差是以真实值为标准,偏差是以多次测量结果的平均值为标准。
误差与偏差的含义不同,必须加以区别。但是由于在一般情况下,真实值是不知道的(测量的目的就是为了测得真实值),因此处理实际问题时常常在尽量减小系统误差的前提下,把多次平行测量值当作真实值,把偏差当作误差。
残差(residual)
观察值与模型估计值之间的差。以回归分析为例,回归方程y=b0+b1x,当知道b0和b1时这就是一个真实的回归模型。比如y=2+3x。取一个数值(1,2),则模型估计值为y=2+3×1=5。残差为2-5=-3。因此,只要有一个确定的取值以及模型,则模型肯定有一个估计值,也就有一个残差了。对残差进行分析是回归分析的一个重要部分。
方差(Variance)
预测值之间的离散程度,也就是离其期望值的距离。方差越大,数据的分布越分散。1
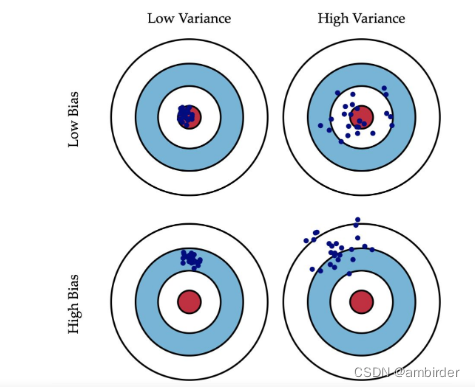
通俗易懂方差(Variance)和偏差(Bias) ↩︎
最后
以上就是冷酷毛衣最近收集整理的关于数据统计基础知识误差(error)偏差(Bias)残差(residual)方差(Variance)的全部内容,更多相关数据统计基础知识误差(error)偏差(Bias)残差(residual)方差(Variance)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复