机器学习第九周（四）--推荐系统预测电影评分基于内容的推荐协同过滤协同过滤的优化低秩矩阵分解均值归一化

预测电影评分

推荐系统的引入主要有俩个原因：

1、推荐系统是机器学习中一个很重要的应用，一些大的商业公司会利用推荐系统来提高商业效益，这是很重要的。
2、能够自动学习新特征。当我们采用一种算法来自动学习到新特征时，比手动设计特征效率要搞得多，推荐系统能提供这样的效果。

以一个对电影评分的例子说明：

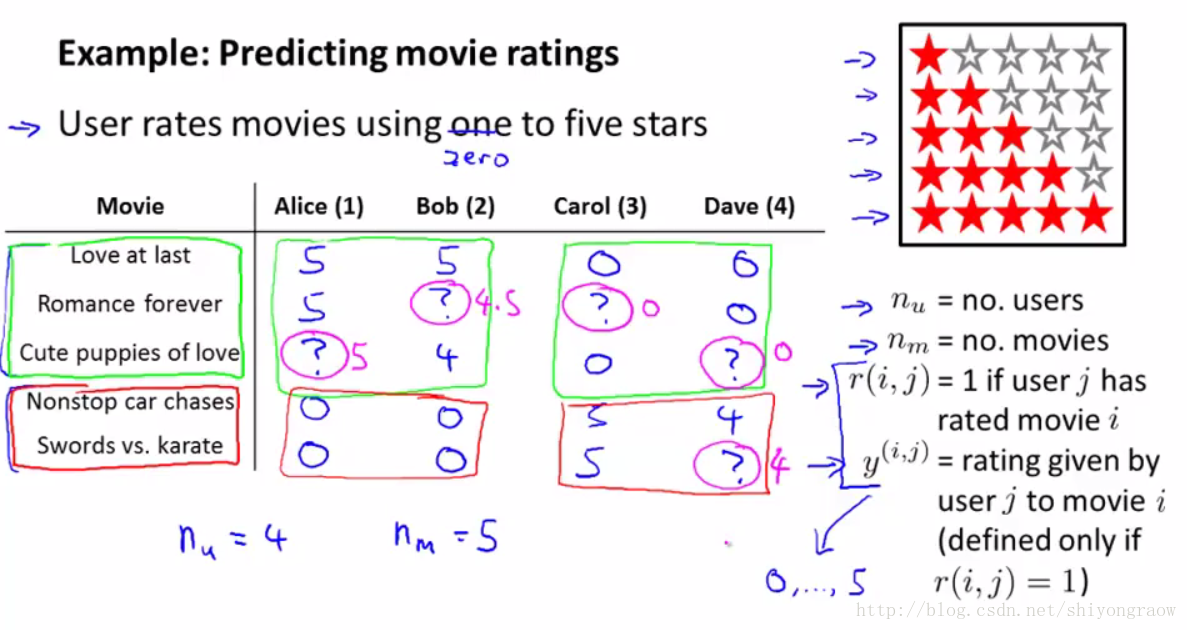
$n_u$表示评分人数，这里是四人。
$n_m$表示电影数量，这里是五部电影。
$r(i,j)$表示用户$j$对电影$i$的评分。如果评过分，则$r(i,j)=1$，否则为0.
$y^{(i,j)}$表示用户$j$对电影$i$评分分值，当然，只有在$r(i,j)=1$时，$y^{(i,j)}$才有值。

推荐系统要做的就是根据给定的$r(i,j)$和$y^{(i,j)}$，去对未评分的电影作出预测（如图中的“？”处）。

基于内容的推荐

构造特征向量

为了预测用户$j$对电影$i$的评分，我们给定一个参数向量$theta$（后面会阐述这个向量具体怎么来的），并有特征向量$x^{(i)}$，这里只给出$x_1$和$x_2$俩个特征，同理，我们可以加入$x_0=1$。
这样，我们预测用户$j$对电影$i$的评分通过公式$(theta^{(j)} )^TX^{(i)}$得到。如预测第一个用户对第三部电影的评分。预测结果是4.95。

参数向量$theta$的计算

$m^{(j)}$ 表示用户$j$评定过的电影数量。

根据上图公式，最小化$theta^{(j)}$就得到我们上面预测需要的参数向量（$m^{(j)}$ 是常数，不影响最后的最小化结果，所以去掉）。这只是我们其中一位用户的参数向量，当需要所有用户的参数向量时，即是对所有用户求和。结果如下。

1、$i:r(i,j)=1$ 表示评过分的人数。
2、正则项这里同样是从1开始的。

梯度下降

如何最小化theta呢？这里还是采用梯度下降。

综上，我们已知不同电影的特征，根据这些特征来进行预测，这常称作“基于内容的推荐”算法。但是，对于一些电影我们很难去得到这些特征，下面将阐述这种问题的做法。

协同过滤

特征向量

上面我们说过，有些时候特征难以选择，如果算法能自动选择特征那就相当好了，其中之一就有协同过滤。

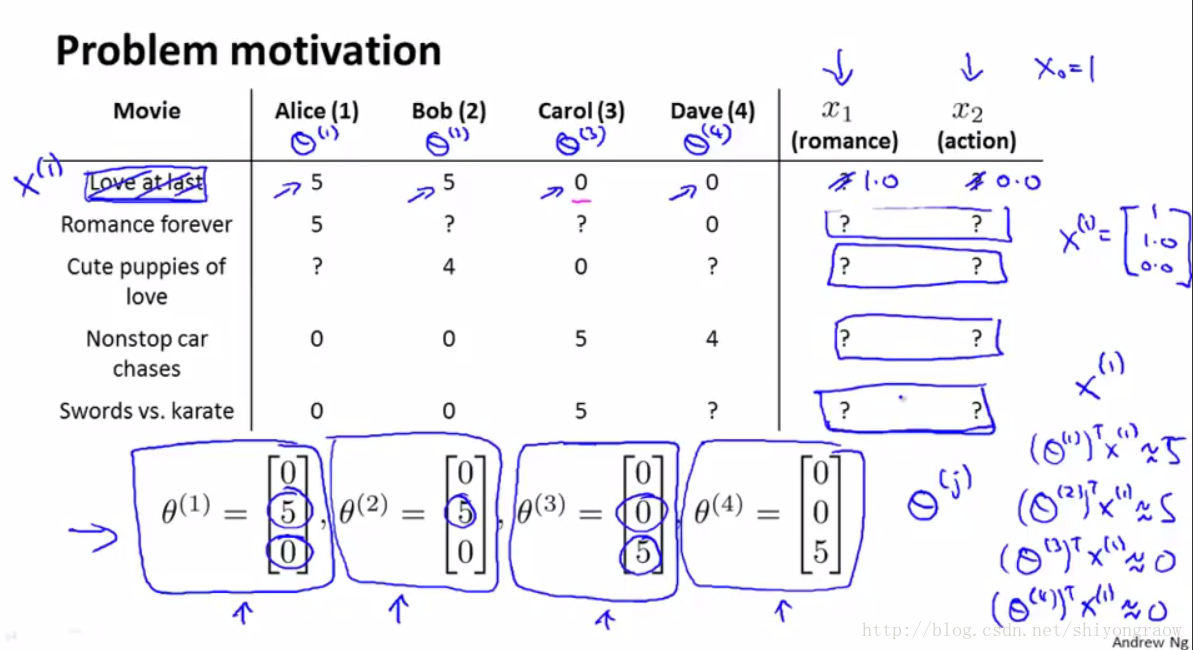
在这里，我们只知道有$x_1$和$x_2$俩个特征，但具体数值多少我们并不知道，我们也无法从电影名字去推断这个特征。
以用户1为例，我们只知道他的$theta^{(1)}=[0,5,0]^T$，即他非常喜欢爱情电影，但不喜欢动作电影。用户2、3、4同样也给出参数向量$theta^{(i)}$。
即根据参数向量$theta$和每个用户对每部电影的具体评分，我们可以推出每部电影的具体特征向量。

具体的，我们有如下，而且可以计算所有电影的特征向量：

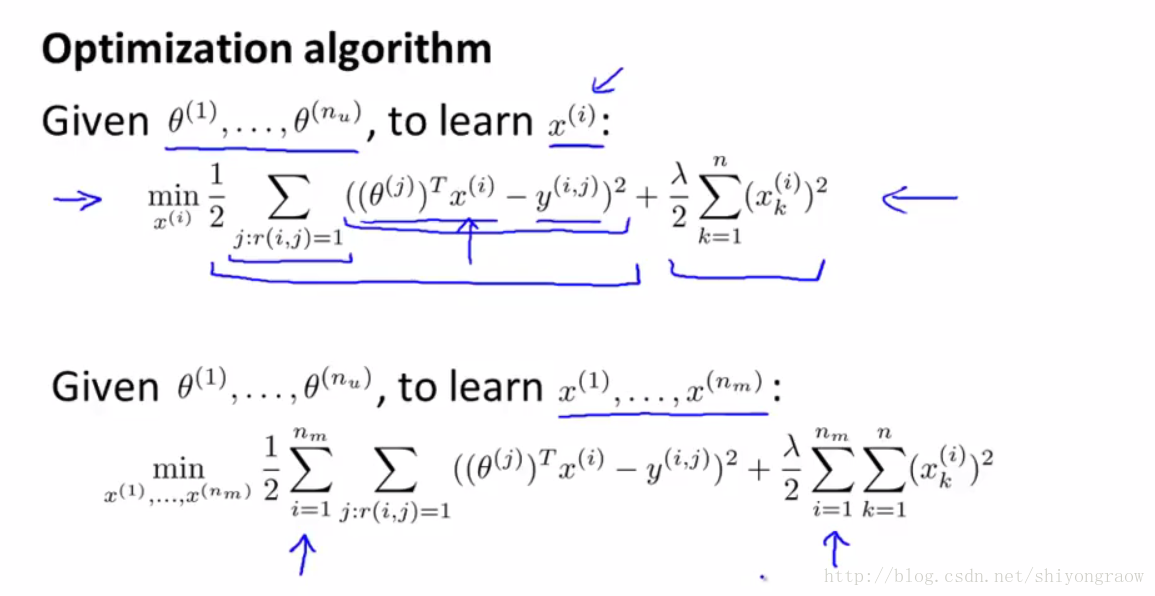
矛盾？？？

前面我们讲过根据特征向量$x$可以得出最优的$theta$向量，这一节又提出根据$theta$向量来求最优特征向量$x$，这貌似是一个鸡生蛋和蛋生鸡的问题，作者这里给出方法是先随机一个$theta$，然后根据$theta$最优化$x$，再根据$x$最优化$theta$，不断迭代，直到收敛。

综上就是简单的协同过滤算法，当你针对一大批用户数据执行这个算法时，这些用户实际上在高效地进行了协同合作来得到每个人对电影的评分值。只要用户对某几部电影进行评分，每个用户就都在帮助算法更好的学习出特征。这样以来，通过自己对几部电影评分之后，我就能帮助系统更好的学习到特征。这些特征可以被系统运用，为其他人做出更准确的电影预测。

协同过滤的优化

协同过滤的优化

如上面所说，我们需要不断地在$x$和$theta$之间折腾，很繁琐，我们把俩个公式结合一下。

1、1、2俩个式子中红框部分其实是一样的，综合起来得到第三个式子的红框中。$(i,j):r(i,j)=1$其实就是对满足$r(i,j)=1$的所有$(i,j)$求和。
2、这里不包括$x_0=1$，即$x$有原定的所有$n$个特征，不会加入新特征。相应地$theta$也就不包括$theta_0$。

协同过滤过程

协同过滤解决问题的一般步骤如下：

1、因为排除$x_0$项，所以这里结果也就没有$k=0$项。
2、初始化的过程是必须要的，作用类似于神经中的对称破坏。

低秩矩阵分解

协同过滤的向量化实现

对上面的协同过滤进行向量化实现

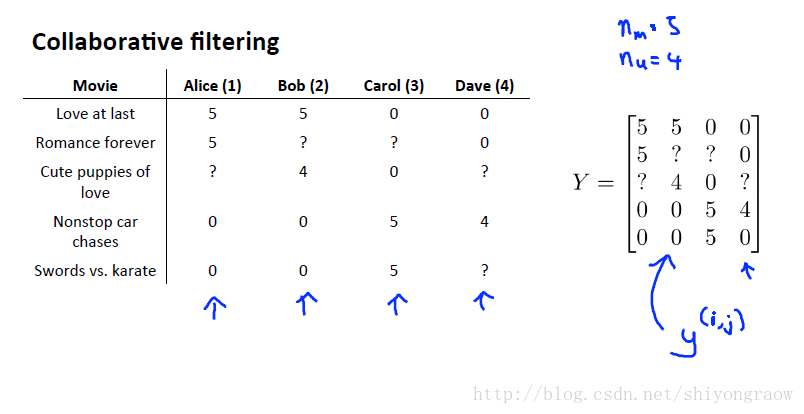
$Y$是评分矩阵。当我们向量化特征向量$X$和$theta$时，最后得出的预测评分矩阵如下。

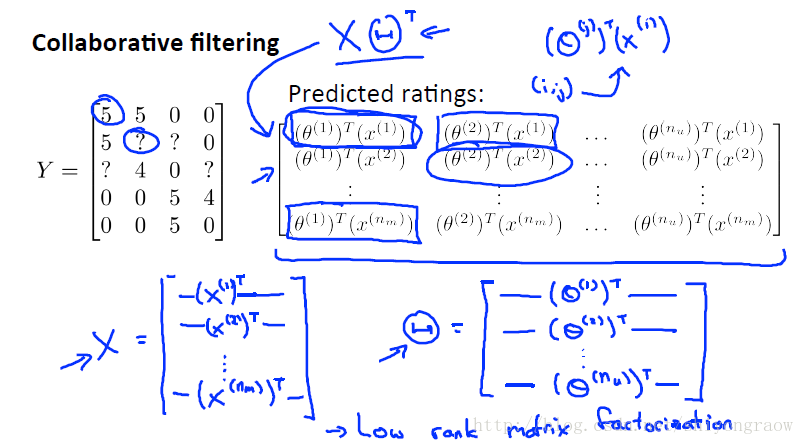
这个预测矩阵可以看做是电影的特征矩阵$X$和用户的参数矩阵$Theta^T$的乘积。
协同过滤算法在代数上也叫低秩矩阵分解。

找相关电影

如何做到针对用户喜欢的某一部电影，然后推荐给他另一部类似的电影呢？

对于每一部电影，都可以找到它的特征向量。
假设我们想找到和电影$i$最类似的一部电影，有一种方式就是求出所有电影的特征向量，然后和电影$i$的特征向量求欧氏距离，距离最小的那个就是最类似的。
同样地，如果想找到5部最相似的电影，你只要求出欧氏距离最小的5部电影即可。

均值归一化

均值归一化的引入

以一个例子引入

我们新增加一个用户，目的用协同过滤算法算法推荐用户电影。
因为用户没有给任何电影评分，因此代价函数前半部分没有满足$r(i,j)=1$的条件，可以忽略，考虑后半部分，最小化这一项的结果是$theta^{(5)} =[0,0,0]^T$。很明显，这样对电影评分的预测都是0，也就意味着不会有电影推荐给他，这样结果明显不好。

均值归一化

还是以上面的为例子，对$Y$矩阵做均值归一化

把归一化后的矩阵称作$mu$，将$Y-mu$作为新的$Y$矩阵，再用这个矩阵去学习参数$theta^{(j)}$和$x ^{(i)}$。

因为归一化过程中减去了均值，所以预测结果要加上均值矩阵$mu$。

用以上方法就能预测出用户5对每个电影的评分。

最后

以上就是美好豌豆为你收集整理的机器学习第九周（四）--推荐系统预测电影评分基于内容的推荐协同过滤协同过滤的优化低秩矩阵分解均值归一化的全部内容，希望文章能够帮你解决机器学习第九周（四）--推荐系统预测电影评分基于内容的推荐协同过滤协同过滤的优化低秩矩阵分解均值归一化所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。