Matlab 加权最小二乘获取转换矩阵一、简介

50 阅读 0 评论 33 点赞

我是靠谱客的博主老实砖头，最近开发中收集的这篇文章主要介绍Matlab 加权最小二乘获取转换矩阵一、简介，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

文章目录

一、简介
二、实现代码
三、实现效果
参考资料

一、简介

通过对两个坐标系中的一些匹配点来寻找两个坐标系之间的关系是一项经典的摄影测量任务，该方式在立体摄影测量和机器人技术中都有应用。

假设我们得到了在两个不同的笛卡尔坐标系中测量的一些点坐标，如下图所示。从这些测量中恢复两个系统之间的转换的摄影测量问题称为绝对定向问题，而绝对方向的问题常用的处理方式主要分为四种：经验型、图论（图形）、数值型以及最后的迭代方式。这里采用的是数值型的求解方式。

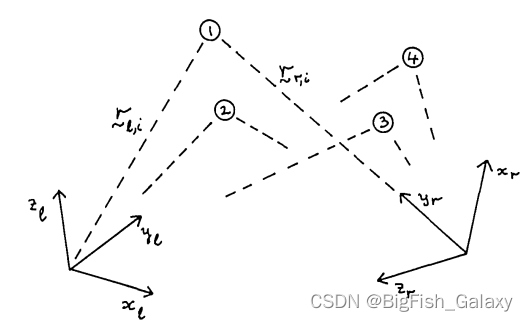
一般而言，两个笛卡尔坐标系之间的变换可以被认为是刚体运动的结果，因此可以分解为旋转和平移两个动作。其中，有时候可能会缺少尺度的参与，因为大多数情况下两个坐标系是相同尺度（1个自由度），平移显然有三个自由度，旋转也具有三个自由度（不同轴的旋转角度）。那么两个坐标系中已知的三个点可以提供了9个约束条件(每个点三个坐标)，足以让我们确定7个未知数。但是在实践中，测量往往是不够精确的，因此仅仅使用三个点往往是不能满足要求，需要使用三个以上的点来寻求更高的精度