【二叉树】先序、中序、后序遍历规则和已知两种遍历求另外一种遍历。包教包会！【】一、二叉树先序遍历二、二叉树中序遍历三、二叉树后序遍历四、已知两种遍历求另外一种遍历（也是求原二叉树）

一、二叉树先序遍历

1、先序遍历的访问过程（根左右）

(1)先访问根节点
(2)先序遍历根节点的左子树
(3)先序遍历根节点的右子树

2、流程图及原理解释

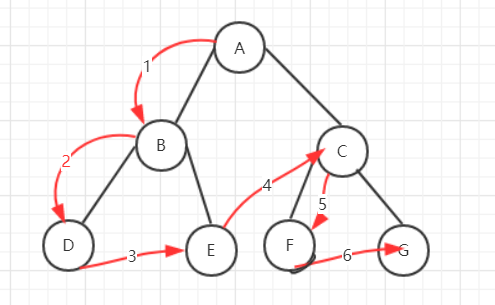
先序遍历流程图解释：
由于先序遍历先访问的是根节点，所以先访问的是根节点A，再访问左节点B，由于左节点B仍然是一个根节点，所以继续访问的是根节点B的左节点D，由于D没有左右结点，所以再访问B的右节点E。E访问完之后，A的左子树算是全部访问完毕，再访问A的右子树，道理与前述相同，不再重复。

3、前序遍历递归代码

/** 先序遍历*/
void Pre_Order(BinTNode *T1)
{
    if(T1 != NULL)
    {
        printf("%c  ",T1->data);
        Pre_Order(T1->Lchild);
        Pre_Order(T1->Rchild);
    }
}

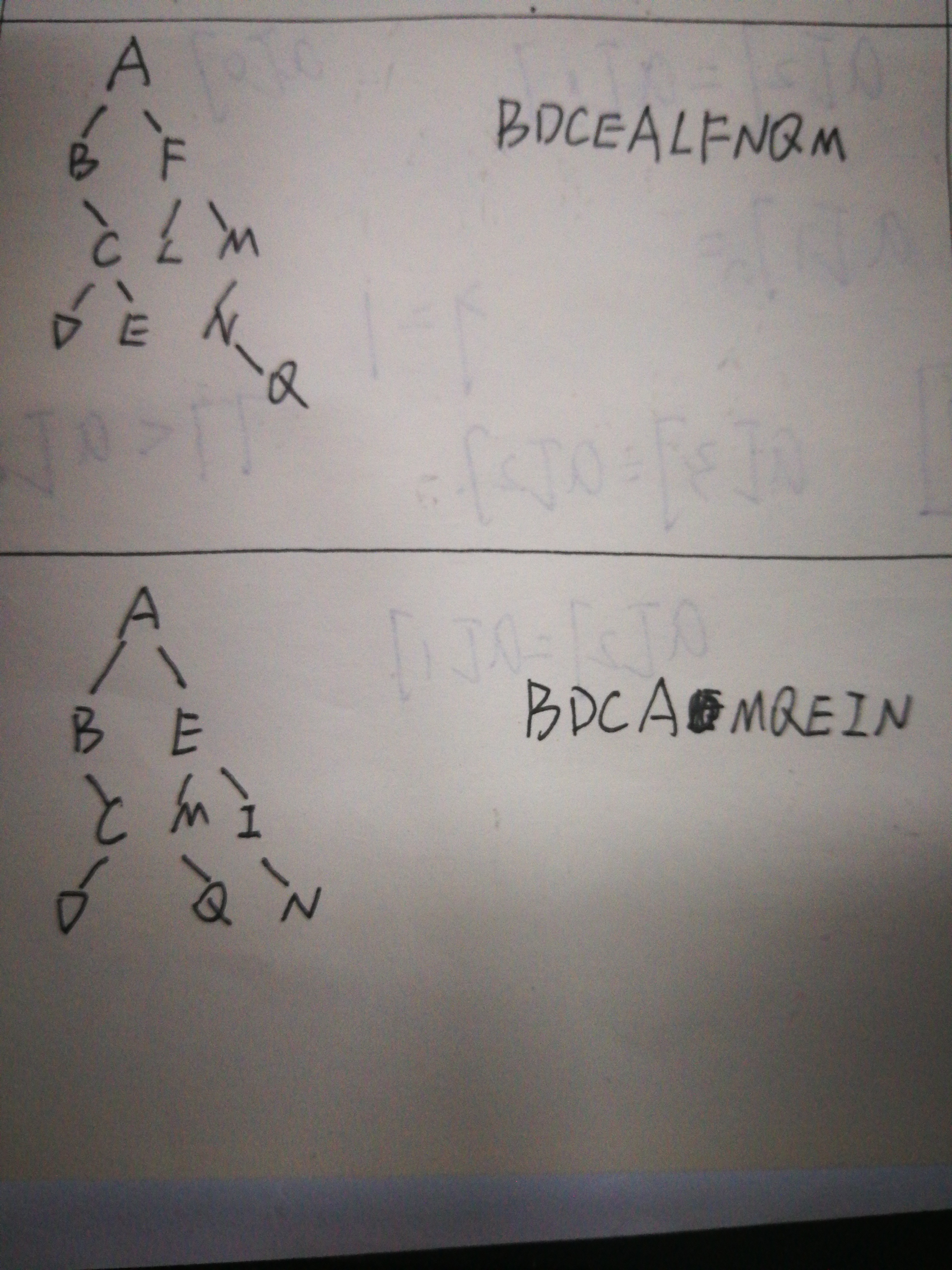
4、前序遍历练习题（由于图太难画改用手绘^_^嘻嘻）

附带答案大家自己领会（其实是因为我懒）

二、二叉树中序遍历

1、中序遍历的访问过程（左根右）

(1)中序遍历根节点的左子树
(2)再访问根节点
(3)中序遍历根节点的右子树

2、流程图及原理解释

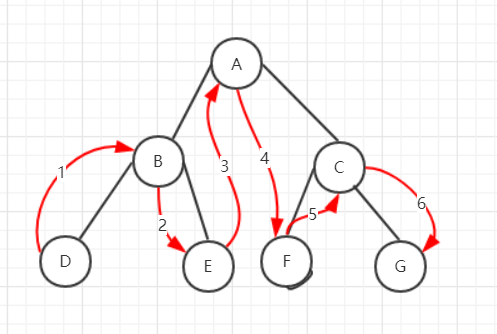
中序遍历流程图解释：
由于中序遍历先访问的是左节点，所以从最左边的开始遍历，即从D开始遍历。然后再访问D的根节点E.此时根节点A的左子树已经访问完毕，然后再访问左子树的根节点也就是A，然后再按照左根右的顺序继续访问右子树。这里不再重复。

3、中序遍历递归代码

/** 中序遍历*/
void Mid_Order(BinTNode *T1)
{
    if(T1 != NULL)
    {
        Mid_Order(T1->Lchild);
        printf("%c  ",T1->data);
        Mid_Order(T1->Rchild);
    }
}

4、中序遍历练习题（由于图太难画再次改用手绘^_^嘻嘻）

附带答案大家自己领会（其实是因为我懒）

三、二叉树后序遍历

1、后序遍历的访问过程（左右根）

(1)后序遍历根节点的左子树
(2)后序遍历根节点的右子树
(3)最后访问根节点

2、流程图及原理解释

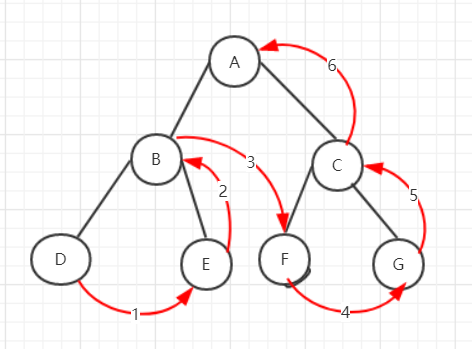
后序遍历流程图解释：
由于后序遍历根节点是最后访问所以先访问D，然后访问B的右子树也就是E，左右子树都访问完之后再访问二者的根节点B，此时不是立即访问根节点A，而是访问A的右子树，直到左右子树都访问完毕后，再访问根结点A。

3、后序遍历递归代码

/** 后序遍历*/
void Beh_Order(BinTNode *T1)
{
    if(T1 != NULL)
    {
        Beh_Order(T1->Lchild);
        Beh_Order(T1->Rchild);
        printf("%c  ",T1->data);
    }
}

4、后序遍历练习题（由于图太难画还是改用手绘^_^嘻嘻）

附带答案大家自己领会（其实是因为我懒）

四、已知两种遍历求另外一种遍历（也是求原二叉树）

1、已知先序和中序求原二叉树并写出后序

先序：ABCDEFGH
中序：BDCEAFHG
解题步骤：（中序确定左右子树、先序确定根节点）
①首先确定根节点 先序中最先出现的是根节点 所以确定A是根节点
②根据中序确定根节点A的左右子树 BDCE是A的左子树 FHG是A的右子树
③然后与A相连的左子树的根节点是什么呢？刚才说到越靠前的越是根节点，所以A的左子树的根节点是在先序中最先出现的B，然后再根据中序可以知道DCE是B的右子树，那么该右子树的根结点有是什么，再次回到先序中确定C是一个根节点。以此类推、、、、、

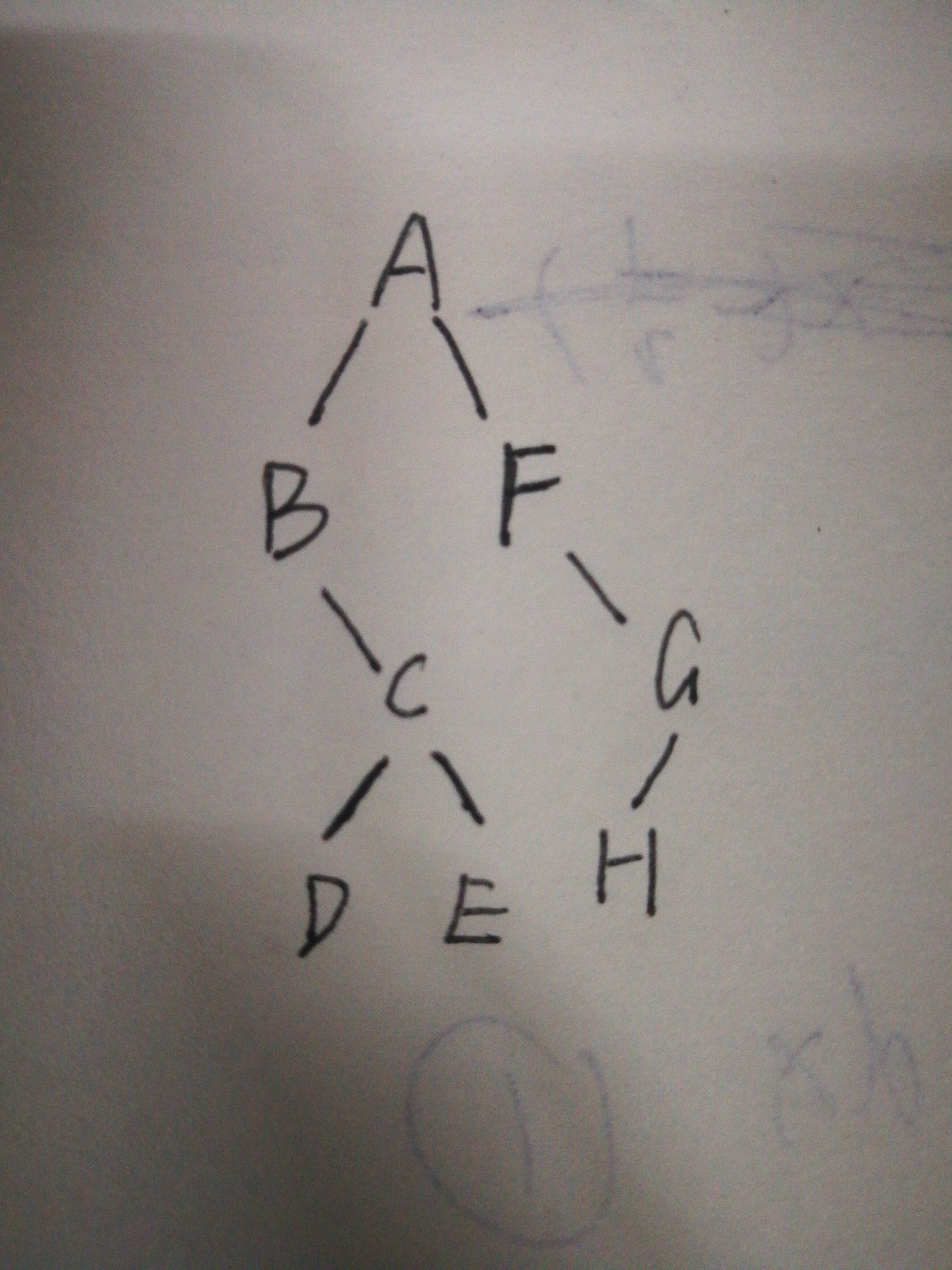
所以答案是：后序 DECBHGFA

2、已知中序和后序求原二叉树并写出前序

中序：BDCEAFHG
后序：DECBHGFA
解题步骤：（中序确定左右子树、后序确定根节点）
①首先确定根节点 后序中最晚出现的是根节点 所以确定A是根节点
②根据中序确定根节点A的左右子树 BDCE是A的左子树 FHG是A的右子树
③然后与A相连的左子树的根节点是什么呢？刚才说到越靠后的越是根节点，所以A的左子树的根节点是在后序中最晚出现的B，然后再根据中序可以知道DCE是B的右子树，那么该右子树的根结点有是什么，再次回到后序中确定C是一个根节点。以此类推、、、、、

所以答案是：先序 ABCDEFGH

小伙伴们如果还有问题可以加 企鹅1577655659 继续讨论哦！
溜了溜了~~

最后

以上就是微笑小懒虫为你收集整理的【二叉树】先序、中序、后序遍历规则和已知两种遍历求另外一种遍历。包教包会！【】一、二叉树先序遍历二、二叉树中序遍历三、二叉树后序遍历四、已知两种遍历求另外一种遍历（也是求原二叉树）的全部内容，希望文章能够帮你解决【二叉树】先序、中序、后序遍历规则和已知两种遍历求另外一种遍历。包教包会！【】一、二叉树先序遍历二、二叉树中序遍历三、二叉树后序遍历四、已知两种遍历求另外一种遍历（也是求原二叉树）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。