前言
循环神经网络(Recurrent Neural Network,RNN)与卷积神经网络一样,都在深度学习中占有非常重要的地位。虽然先前笔记提到的全连接网络和卷积神经网络已经有很强的表示能力了,但由于网络结构的限制,它们只能处理定长的输入数据,并且由于有向无环的特点,它们只通过当前输入数据预测输出,而不考虑输入数据的前后顺序、也不考虑前后数据是否有关联。而文本、语音和视频等序列式数据,往往都是不定长的、并且前后数据相关性极大,一旦改变顺序,往往会失去原先的信息。所以需要一种考虑输入数据顺序,并且能够记忆以往数据信息的网络——循环神经网络。这篇笔记将学习最简单的循环神经网络RNN的原理和Pytorch的RNN层。
本笔记主要参考深度之眼Pytorch课程、torch官方文档、孙玉林等著的PyTorch深度学习入门与实战和慕课网深度学习之神经网络(CNN/RNN/GAN)算法原理+实战课程。所用数据来源于网络,文本是根据笔者对诸多课程的粗浅理解而写,如果有朋友发现错误,还望不吝指出。另外,发现有人在其他平台照搬笔者笔记,不仅不注明出处,有甚者更将其作为收费文章,因此笔者将在文中任意位置插入识别标志,若影响阅读,还望见谅。
线性层见:深度之眼Pytorch打卡(十三):Pytorch全连接神经网络部件——线性层、非线性激活层与Dropout层
RNN与其他网络对比
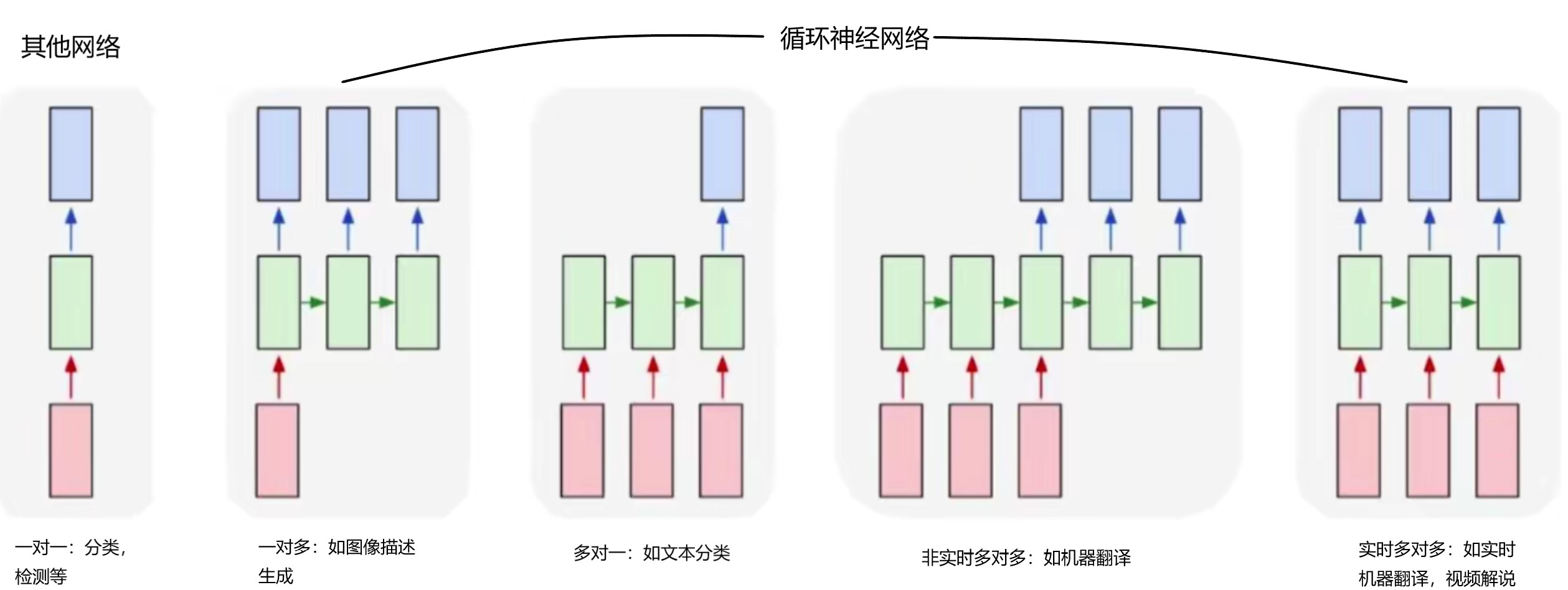
全连接神经网络和卷积神经网络适合的分类、检测等任务,其输入只有一个,或是一幅图像,或是一组特征,其输出也只有一个,或是一个预测值,或是一个类别向量。由于网络结构的限制(矩阵乘法要求维度对应),他们的输入必须被 resize 到指定大小,只要网络结构被确定,其输出尺寸也将被确定,结构示意图如图1所示,改自图源。
循环神经网络与上述两者并无本质差别,模型单元的输入输出也是定长的。使得循环神经网络具有输入输出不定长,并且对以往数据有“记忆” 的原因是:它是有环的。通过循环调用模型单元,来实现不定长输入序列的处理,每循环一次,模型单元就处理一个定长的序列元素,如字符串中的 一个字符,循环次数由输入数据序列中元素的个数决定。每调用一次模型单元,都会产生两个输出——当前预测值和状态值,当前状态值在加权后参与下一个状态值的产生,即当前输入元素会对下一个输入元素的状态值有影响,进而会对其输出预测值有影响,RNN用状态值来实现所谓 “记忆”。模型单元循环了多少次,就会产生多少个输出预测值,最后根据任务要求选用其中若干个组成序列,作为模型的输出,就实现了输出序列不定长。结构示意图如图1所示,改自图源,根据不同的任务,循环神经网络可以灵活的调整其输入输出尺寸。
RNN原理及简单实例应用
-
RNN原理
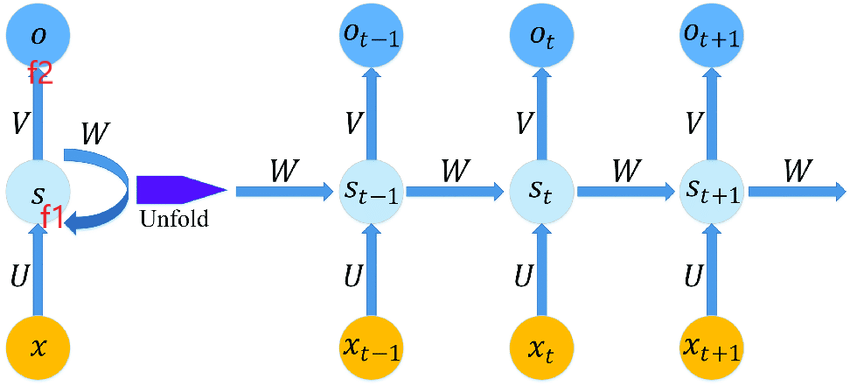
RNN模型单元,一般是由三个线性层和两个非线性激活层构成,如图2所示,图左右是循环收拢与展开的关系,改自图源。 输出 O 之前有一个非线性激活层f2,状态值 S 之前有一个非线性激活层f1。输入到f1之间包含一个线性层,权值矩阵为U,上一个状态值到f1之间包含一个线性层,权值矩阵为W。当前状态值 S 到非线性激活层之间包含一个线性层,权值矩阵为V 。使用时,根据输入中包含数据单元的个数,来决定模型单元被调用的次数,每次产生的状态值都会被加权后往后传。模型单元表达式如式(1)和式(2)所示。
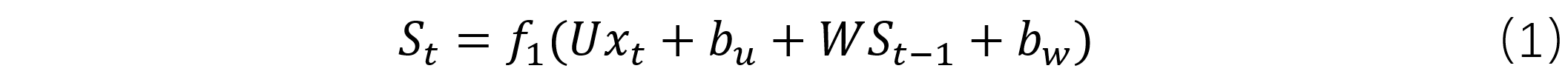
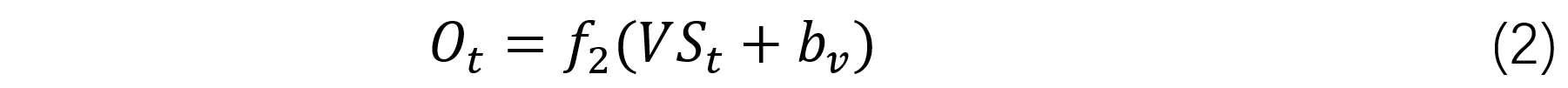
-
RNN简单实例应用
用一个在输入法中很常见的,下一个输入字符预测超级简化模型训练来做进一步学习。现在假设所有样本中只包含4种(实际需要统计)不同的字符,h、e、l、o,并且模型只预测这4个字符(实际常常128),即分4类,流程图如图3,改自图源。
用一个长度为4的向量,就可以正交的表示4个字符,设o=[1 0 0 0], h=[0 1 0 0]、e=[0 0 1 0],l=[0 0 0 1],4就是模型单元的输入尺寸,也就是线性层1的输入尺寸,单个字符就是模型单元的输入。实际应用中,式(1)和(2)中的f1常用tanh,是多元分类,f2用softmax。从图中可以看出,模型单元的输入尺寸为(4,1),线性层1的权值矩阵U的shape为(3,4),线性层2的权值矩阵W的shape为(3,3)。4分类,故输出尺寸为4,易得线性层3的权值矩阵V的shape为(4,3),由上述尺寸和激活函数就可以定义出模型单元的基本结构。循环调用模型单元去处理输入序列中的字符,每处理一个字符都能得到一个关于下一个字符的预测和能“记忆”含有当前及以往信息的状态值”。最小化预测值与标签之间的距离,就可以建立输入了的字符,与下一个被希望出现字符之间的映射关系,其本质是向量之间的映射关系。
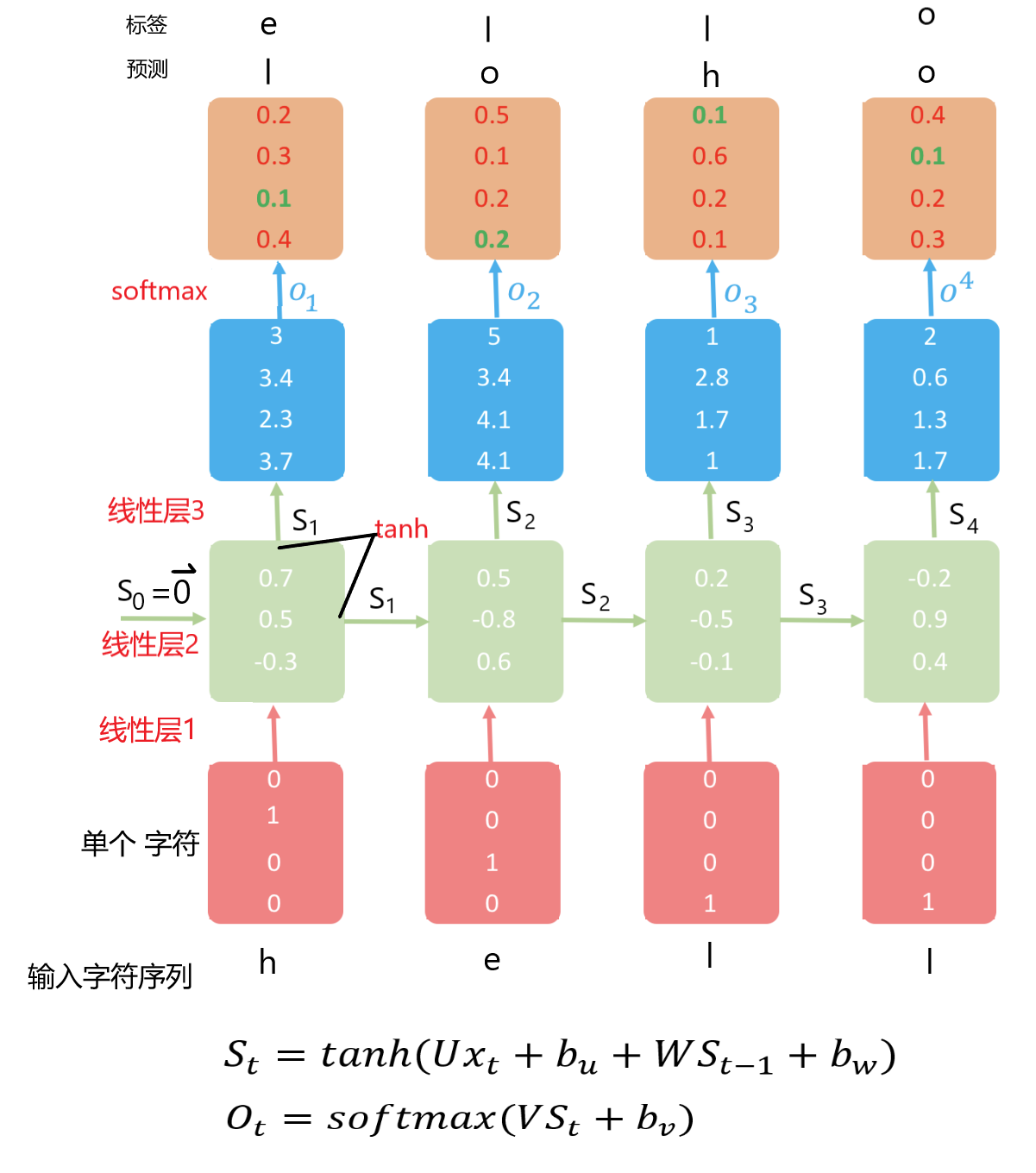
每一个预测输出与标签之间的损失之和就是总的损失,梯度下降时使用该损失。值得注意的是,模型单元被循环调用的过程中U,V,W是一直不变的,所以反向传播梯度下降求导时,是被复合过很多次的函数对U,V,W求偏导数,用类似图4所示的链式求导法则结构,图源。
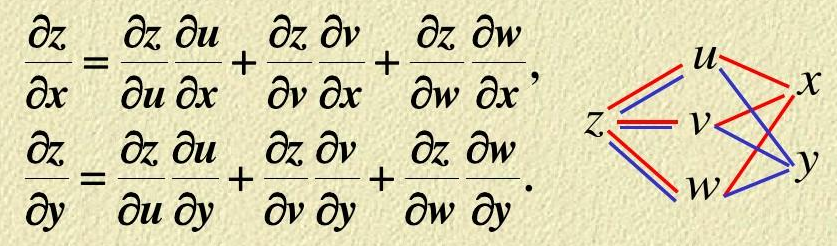
上述过程可以用以下代码实现,关键在于构建三个线性层,和状态值在循环过程中的传递。对于中国这个简单的任务,不需要迭代多少次就可以完全预测正确。
import torch
import torch.nn as nn
# 数据序列
in_seq = ['h', 'e', 'l', 'l', 'o']
# 字符one-hot编码
char2vec = {
'o': [1, 0, 0, 0],
'h': [0, 1, 0, 0],
'e': [0, 0, 1, 0],
'l': [0, 0, 0, 1]
}
# 字符索引
char2idx = [key for key in char2vec.keys()]
# 输入序列与标签one-hot编码,输入字符的后一个字符为标签
input_data = [char2vec[seq] for seq in in_seq[:len(in_seq) - 1]]
input_data = torch.tensor(input_data, dtype=torch.float)
target = [char2vec[seq] for seq in in_seq[1:len(in_seq)]]
target = torch.tensor(target, dtype=torch.float)
print('Input:n', input_data)
print('Target:n', input_data)
# 初始状态
S = torch.randn(3, dtype=torch.float)
loss = 0
# RNN
U_Linear = nn.Linear(4, 3, bias=True)
V_Linear = nn.Linear(3, 4, bias=True)
W_Linear = nn.Linear(3, 3, bias=True)
tanh = nn.Tanh()
softMax = nn.Softmax(dim=0)
# 损失函数
Loss_function = nn.MSELoss()
# 三个线性层各一个优化器
optimizer = torch.optim.SGD(U_Linear.parameters(), lr=0.5)
optimizer1 = torch.optim.SGD(V_Linear.parameters(), lr=0.5)
optimizer2 = torch.optim.SGD(V_Linear.parameters(), lr=0.5)
# 迭代100次
for n in range(30):
for i in range(len(input_data)): # 循环读取输入序列中元素
# RNN模型单元前向传播
U_out = U_Linear(input_data[i])
W_out = W_Linear(S)
S = tanh(U_out + W_out)
V_out = V_Linear(S)
outputs = softMax(V_out)
# 计算总的损失
loss = loss + Loss_function(outputs, target[i])
predicts = list(torch.round(outputs.data).numpy())
if n % 10 == 0:
idx = predicts.index(max(predicts))
print('Outputs', outputs.detach().numpy(), 'Predict:', char2idx[idx])
if n % 10 == 0:
print('inters:', n, 'Loss:', loss.detach().numpy())
# 清除上一次的梯度
optimizer.zero_grad()
optimizer1.zero_grad()
optimizer2.zero_grad()
# 误差反向传播加优化模型,由于三个线性层单独进行的优化,所以保留了计算图
loss.backward(retain_graph=True)
optimizer.step()
optimizer1.step()
optimizer2.step()
loss = 0
# (CSDN意疏原创笔记:https://blog.csdn.net/sinat_35907936/article/details/107833112)
输出:
Input:
tensor([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.]])
Target:
tensor([[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.]])
Outputs [0.290094 0.16060394 0.36847702 0.18082501] Predict: o
Outputs [0.2719248 0.19114026 0.36937279 0.16756214] Predict: o
Outputs [0.27425763 0.16854036 0.3864712 0.17073087] Predict: o
Outputs [0.26531443 0.17352623 0.39586946 0.16528983] Predict: o
inters: 0 Loss: 0.793978
Outputs [0.194226 0.08887551 0.4478625 0.269036 ] Predict: o
Outputs [0.19685005 0.09957253 0.14356932 0.5600081 ] Predict: l
Outputs [0.21975377 0.09972848 0.2541498 0.4263679 ] Predict: o
Outputs [0.2219655 0.1078726 0.22906095 0.44110093] Predict: o
inters: 10 Loss: 0.50040627
Outputs [0.13650393 0.04120047 0.74463063 0.07766501] Predict: e
Outputs [0.12212814 0.05029681 0.0703768 0.7571983 ] Predict: l
Outputs [0.20788915 0.05729144 0.06590841 0.668911 ] Predict: l
Outputs [0.35238904 0.08350334 0.19499636 0.36911124] Predict: o
inters: 20 Loss: 0.23350757
# (CSDN意疏原创笔记:https://blog.csdn.net/sinat_35907936/article/details/107833112)
RNN层
CLASStorch.nn.RNN(*args, **kwargs)
- 参数
input_size – The number of expected features in the input x
hidden_size – The number of features in the hidden state h
num_layers – Number of recurrent layers. E.g., setting would mean stacking two RNNs together to form a stacked RNN, with the second RNN taking in outputs of the first RNN and computing the final results. Default: 1num_layers=2
nonlinearity – The non-linearity to use. Can be either or . Default: ‘tanh’‘relu’‘tanh’
bias – If , then the layer does not use bias weights b_ih and b_hh. Default: FalseTrue
batch_first – If , then the input and output tensors are provided as (batch, seq, feature) instead of (seq, batch, feature). Note that this does not apply to hidden or cell states. See the Inputs/Outputs sections below for details. Default: TrueFalse
dropout – If non-zero, introduces a Dropout layer on the outputs of each RNN layer except the last layer, with dropout probability equal to . Default: 0dropout
bidirectional – If , becomes a bidirectional RNN. Default: TrueFalse
- pytorch RNN层应用实例
import torch.nn as nn
import torch
# 数据序列
in_seq = [['h', 'e', 'l', 'l', 'o'],
['l', 'o', 'o', 'h', 'e']]
# 字符one-hot编码
char2vec = {
'o': [1, 0, 0, 0],
'h': [0, 1, 0, 0],
'e': [0, 0, 1, 0],
'l': [0, 0, 0, 1]
}
# 字符索引
char2idx = [key for key in char2vec.keys()]
batch_size = 2
seq_len = 5
in_size = 4
hi_size = 3
num_layers = 1
out_size = 4
in_ = []
target = []
# 输入序列与标签one-hot编码,输入字符的后一个字符为标签
for bs in range(batch_size):
tmp = [char2vec[seq] for seq in in_seq[bs][:seq_len - 1]]
in_.append(tmp)
tmp = [char2vec[seq] for seq in in_seq[bs][1:seq_len]]
target.append(tmp)
in_ = torch.Tensor(in_)
target = torch.tensor(target, dtype=torch.float)
print('Input:n', in_)
print('Target:n', target)
# 模型
rnn = nn.RNN(in_size, hi_size, num_layers, batch_first=True)
# rnn层的输出只是隐藏状态,如要实现预测,还需要至少加一个线性层
fc = nn.Linear(hi_size, out_size, bias=True)
softmax = nn.Softmax(dim=2)
# 损失函数
loss_fun = nn.MSELoss()
# 优化器
optimizer = torch.optim.SGD(rnn.parameters(), lr=10)
optimizer1 = torch.optim.SGD(fc.parameters(), lr=10)
# 训练
iters = 30
h0 = torch.randn(num_layers, batch_size, hi_size)
for iter_ in range(iters):
out_put, hn = rnn(in_, h0)
out_put = softmax(fc(out_put))
pred = []
# one-hot编码转字符
for bs in range(batch_size):
pred.append([char2idx[int(torch.argmax(out))] for out in out_put[bs]])
loss = loss_fun(out_put, target)
if iter_ % 10 == 0:
print('Iters: ', iter_)
print('Loss: ', loss)
print('Predict: ', pred)
optimizer.zero_grad()
optimizer1.zero_grad()
loss.backward(retain_graph=True)
optimizer.step()
optimizer1.step()
# (CSDN意疏原创笔记:https://blog.csdn.net/sinat_35907936/article/details/107833112)
输出:
Input:
tensor([[[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.]],
[[0., 0., 0., 1.],
[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.]]])
Target:
tensor([[[0., 0., 1., 0.],
[0., 0., 0., 1.],
[0., 0., 0., 1.],
[1., 0., 0., 0.]],
[[1., 0., 0., 0.],
[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.]]])
Iters: 0
Loss: tensor(0.1805, grad_fn=<MseLossBackward>)
Predict: [['o', 'l', 'o', 'l'], ['l', 'l', 'l', 'l']]
Iters: 10
Loss: tensor(0.0993, grad_fn=<MseLossBackward>)
Predict: [['e', 'l', 'o', 'o'], ['o', 'o', 'o', 'e']]
Iters: 20
Loss: tensor(0.0258, grad_fn=<MseLossBackward>)
Predict: [['e', 'l', 'l', 'o'], ['o', 'o', 'h', 'e']]
# (CSDN意疏原创笔记:https://blog.csdn.net/sinat_35907936/article/details/107833112)
手撕RNN
如果想完全手撕RNN代码,可以去看李沐老师的动手学深度学习第二版,8.5节,循环神经网络从零开始实现。
最后
以上就是落寞小懒虫最近收集整理的关于深度之眼Pytorch打卡(十七):循环神经网络部件——RNN详细原理与pytorch的RNN层应用实例的全部内容,更多相关深度之眼Pytorch打卡(十七):循环神经网络部件——RNN详细原理与pytorch内容请搜索靠谱客的其他文章。








发表评论 取消回复