使用循环神经网络(RNN)实现简易的二进制加法器

利用python实现简易的循环神经网络，并在一个小demo（8比特二进制加法器）上进行了验证，激活函数为logistic函数，利用反向传播算法进行训练。具体的算法原理以及公式推导可参考相关的文献：《深度学习》、Recurrent nets and LSTM等。

相关的源码以及数据集可在链接中进行下载。

rnn.py

# -*- coding: utf-8 -*-

"""
简易的RNN模型实现
"""
import numpy as np


class rnn():

    def __init__(self):
        self.eb = 200           # 误差容限
        self.eta = 0.0001       # 学习率
        self.maxiter = 2000     # 最大迭代次数
        self.errlist = []       # 误差列表
        self.acclist = []       # 测试精度
        self.data = None        # 数据集
        self.label = None       # 标记集
        self.nSampNum = 0       # 样本集行数
        self.nSampDim = 0       # 样本维度
        self.nHidden = 16       # 隐含层神经元
        self.nOut = 1           # 输出层
        self.iterator = 0       # 最优时迭代次数
        self.hide_wb = None     # 隐含层模型参数
        self.tseq_wb = None     # 时序模型参数
        self.out_wb = None      # 输出层模型参数
        self.time = 0

    def fit(self, X, y, Xx, Yy):
        self.nSampNum, self.nSampDim = np.shape(X[0])
        self.time = len(y)
        self.data = np.copy(X)
        self.label = np.copy(y)
        self.hide_wb = 2 * np.random.random((self.nSampDim, self.nHidden)) - 1
        self.out_wb = 2 * np.random.random((self.nHidden, self.nOut)) - 1
        self.tseq_wb = 2 * np.random.random((self.nHidden, self.nHidden)) - 1

        for iter in range(self.maxiter):
            value_out = np.zeros((self.time, self.nSampNum, self.nOut))             # 存储各个时间节点输出层的输出值
            value_hide = np.zeros((self.time+1, self.nSampNum, self.nHidden))       # 存储各个时间节点隐含层的输出值,最后一个时间点作为初始值
            value_loss = np.zeros((self.time, self.nSampNum))                       # 存储各个时间点的误差矩阵

            # 正向传播
            for _t in range(self.time):
                t = self.time - _t - 1       # 从后面的时间节点往前传
                hide_output = self.sigmoid(self.data[t].dot(self.hide_wb) + value_hide[t+1, :, :].dot(self.tseq_wb))
                value_hide[t, :, :] = hide_output
                out_output = self.sigmoid(hide_output.dot(self.out_wb))
                value_out[t, :, :] = out_output

                loss = self.label[t] - out_output.T
                value_loss[t, :] = np.sum(loss, axis=0)
            if self.eb > self.errorfunc(value_loss) or iter == self.maxiter-1:
                self.iterator = iter
                break
            self.errlist.append(self.errorfunc(value_loss))

            pre = self.predict(Xx)
            self.acclist.append(np.sum(pre == Yy) / np.size(pre))
            print('******** iter:', '%4i' % iter, '******** accuracy:', '%.5f' % self.acclist[iter],
                  '******** loss:', '%5f' % self.errlist[iter])
            # 反向传播
            for t in range(self.time):
                # 输出层梯度
                delta_out = np.multiply(value_loss[t, :], self.dlogit(value_out[t, :, :]).T)
                # 隐藏层梯度
                delta_hide = np.multiply(self.out_wb.dot(delta_out), self.dlogit(value_hide[t, :, :]).T)
                # 时序权重梯度
                delta_tseq = np.dot(delta_hide, value_hide[t+1, :, :])

                # 更新梯度权重值
                self.out_wb += self.eta * delta_out.dot(value_hide[t, :, :]).T
                self.hide_wb += self.eta * delta_hide.dot(self.data[t, :, :]).T
                self.tseq_wb += self.eta * delta_tseq.T

    def predict(self, X):
        assert len(X) == self.time
        n, d = np.shape(X[0])
        value_out = np.zeros((self.time, n, self.nOut))  # 存储各个时间节点输出层的输出值
        value_hide = np.zeros((self.time + 1, n, self.nHidden))  # 存储各个时间节点隐含层的输出值,最后一个时间点作为初始值
        for _t in range(self.time):
            t = self.time - _t - 1  # 从后面的时间节点往前传
            hide_output = self.sigmoid(X[t].dot(self.hide_wb) + value_hide[t + 1, :, :].dot(self.tseq_wb))
            value_hide[t, :, :] = hide_output
            out_output = self.sigmoid(hide_output.dot(self.out_wb))
            value_out[t, :, :] = out_output
        pre = 1*(np.sum(np.signbit(-value_out+0.5), axis=2) > self.nOut/2)
        return pre      # 一列为一个样本，一行为预测的序列

    # sigmoid 函数
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    # sigmoid 导函数
    def dlogit(self, output):
        return output * (1 - output)

    # 矩阵各元素平方之和
    def errorfunc(self, inX):
        return np.sum(np.power(inX, 2)) * 0.5

    def TrendLine(self, plt, color='r', type='loss'):
        X = np.linspace(0, self.iterator, self.iterator)
        if type == 'loss':
            Y = np.log2(self.errlist)
        else:
            Y = np.array(self.acclist)
            color = 'g'
        plt.xlabel("iteration")
        plt.ylabel(type)
        plt.plot(X, Y, color)

rnn_test.py

# -*- coding: utf-8 -*-

"""
利用simple-RNN实现简易的二进制加法器
具体功能为：输入两个数的二进制编码，输出两个数之和的二进制表示
"""

from rnn import rnn
import numpy as np
import matplotlib.pyplot as plt


if __name__ == '__main__':
    data = np.load("dataset.npz")
    X = data['data']
    y = data['label']
    sip_rnn = rnn()


    testset = np.load('testset.npz')
    sip_rnn.fit(X, y, testset['data'], testset['label'])

    pre = sip_rnn.predict(testset['data'])
    print('accuracy:', np.sum(pre == testset['label'])/np.size(pre))

    fig = plt.figure()
    ax1 = fig.add_subplot(211)
    sip_rnn.TrendLine(plt, type='accuray')
    ax2 = fig.add_subplot(212)
    sip_rnn.TrendLine(plt)
    plt.savefig('rnn_info.png')
    plt.show()

datasetgen.py

# -*- coding: utf-8 -*-

"""
生成训练样本
"""
import numpy as np


def binary_dict(dim=8):
    """
    :param dim: 二进制的位数
    :return: 十进制数对应二进制数的字典
    """
    up_bound = pow(2, dim)
    int2bindic = {}
    binary = np.unpackbits(np.array([range(up_bound)], dtype=np.uint8).T, axis=1)
    for i in range(up_bound):
        int2bindic[i] = binary[i]
    return int2bindic


def train_set_gen(n=10000, dim=8, name='dataset'):
    """
    :param n: 训练样本个数
    :param dim: 二进制位数
    :return:
    """
    up_bound = pow(2, dim)
    data, label = [], []
    x1 = np.random.randint(up_bound / 2, size=(n, 1), dtype=np.uint8)  # 十进制
    x2 = np.random.randint(up_bound / 2, size=(n, 1), dtype=np.uint8)
    X1 = np.unpackbits(x1, axis=1)                                     # 二进制
    X2 = np.unpackbits(x2, axis=1)
    Y = np.unpackbits(x1+x2, axis=1)

    for i in range(dim):
        data.append(np.stack((X1[:, i], X2[:, i]), axis=1))
        label.append(Y[:, i])
    np.savez(name+".npz", data=data, label=label)

train_set_gen()
train_set_gen(n=100, name='testset')

实验效果图

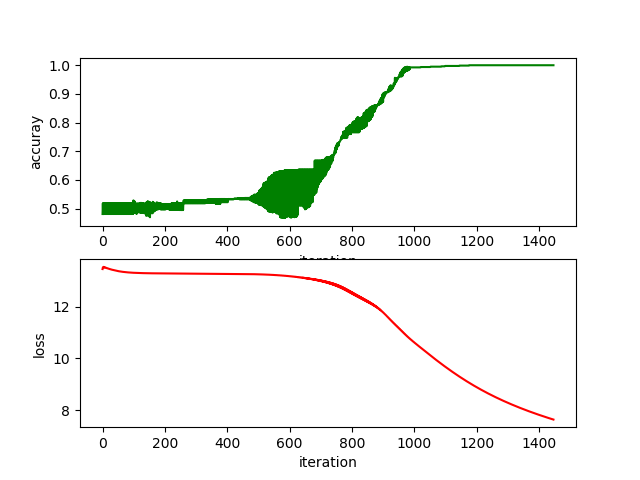
最后

以上就是淡定中心为你收集整理的使用循环神经网络(RNN)实现简易的二进制加法器的全部内容，希望文章能够帮你解决使用循环神经网络(RNN)实现简易的二进制加法器所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。