青蛙跳台阶和汉诺塔非递归实现及汉诺塔详解，附源码一、青蛙跳台阶问题二、汉诺塔问题

53 阅读 0 评论 35 点赞

我是靠谱客的博主风中月亮，最近开发中收集的这篇文章主要介绍青蛙跳台阶和汉诺塔非递归实现及汉诺塔详解，附源码一、青蛙跳台阶问题二、汉诺塔问题，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、青蛙跳台阶问题

题目说明：一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶,例如:
跳上第一级台阶只有一种跳法:直接跳 1 级即可.
跳上两级台阶,有两种跳法: 每次跳 1 级,跳两次; 或者一次跳 2 级.
问要跳上第 n 级台阶有多少种跳法?

1、跳上3级台阶，假如青蛙在第一步时跳1级，那么还剩下2级台阶，2级台阶有2种跳法；假如青蛙在第一步时跳2级，那么还剩下1级台阶，只有一种跳法。跳上3级台阶共有3种跳法。
2、跳上n级台阶，假如青蛙在第一步时跳1级，那么还剩下n-1级台阶，跳法即为F（n-1）；假如青蛙在第一步时跳2级，那么还剩下n-2级台阶，跳法即为F（n-2）；跳上n级台阶跳法F（n) =F（n-1）+F（n-2）。

以下是递归及非递归实现：

//递归实现
int frog_Jump(int n)  
{
	if (n < 3)
		return n;
	return frog_Jump(n - 1) + frog_Jump(n - 2);
}

//非递归实现

int frog_Jump(int n) 
{
	if (n < 3)
		return n;
	int i;
	int a, b, c;
	a = 1;
	b = 2;
	for (i = 3; i <= n; ++i)
	{
		c = a + b;
		a = b;
		b = c;
	}
	return c;
}

二、汉诺塔问题

三柱汉诺塔

汉诺塔问题是一个经典的数学难题，由 3 个柱子和多个半径不等的圆盘构成，如下图所示：
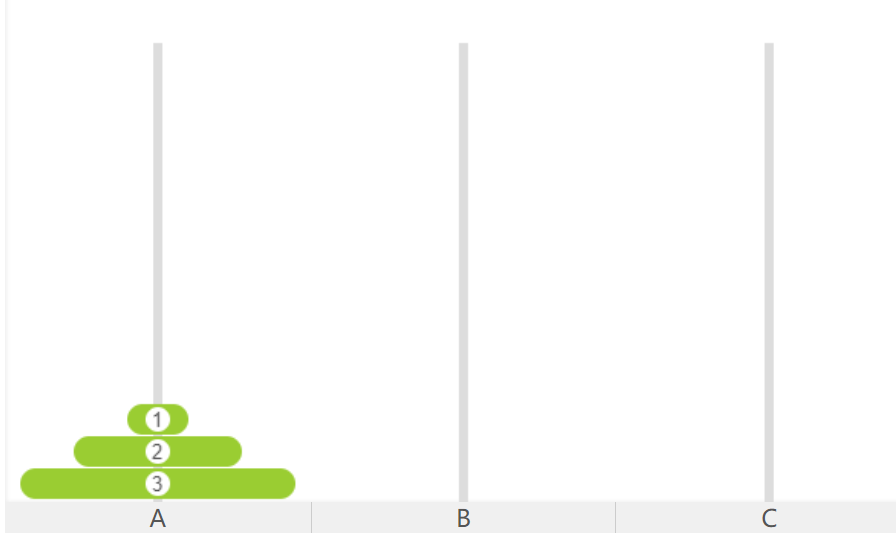
在这里插入图片描述

题目说明：将A柱子中的所有圆盘移动到C柱子，移动过程需遵守以下规则：
1、每次只能移动一个圆盘，而且只能移动某个柱子上最顶部的圆盘；
2、移动过程中，必须保证每个柱子上的大圆盘都位于小圆盘的下面。
如何才能用最少的步数完成该问题？

①当A柱上只有一个圆盘时，显然只需要1步，将圆盘直接移过去。
②当A柱上有2个圆盘时，首先要将小的圆盘先移动到B柱子，再把大的圆盘移动到C柱子，最后把小的圆盘从B柱子移动到C柱子。需要三步。
③当A柱上有3个圆盘时，先把1号圆盘移动到C，再把2号移动到B，然后把1号移动到B，再把3号移动到C，此时的状态如下图：
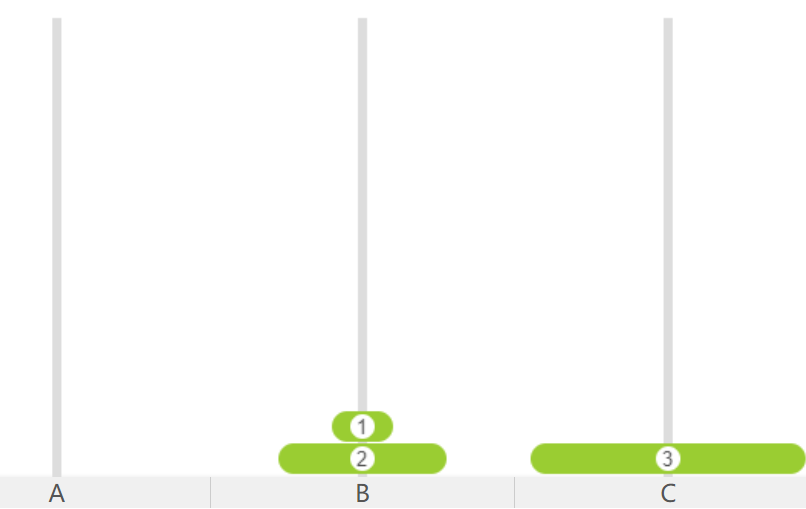
在这里插入图片描述
此时问题就变为把2个圆盘从B移动到C上。与②问题具有相同性质。把1、2两个圆盘看作一个整体，问题就变成3步：首先把(1,2)移动到B柱子，然后把3移动到C柱子，最后把(1,2)移动到C柱子。

设移动盘子数为n，为了将这n个盘子从A杆移动到C杆，可以做以下三步：
(1)以C盘为中介，从A杆将1至n-1号盘移至B杆；
(2)将A杆中剩下的第n号盘移至C杆；
(3)以A杆为中介；从B杆将1至n-1号盘移至C杆。

//递归实现。char a，b,c分别代表A柱、B柱 C柱子
void hanoi(int n, char a, char b, char c) 
{

	if (1 == n)
	{
		printf("从%c--->%cn",a,c);
		return;
	}
	hanoi(n - 1, a, c, b);
	printf("从%c--->%cn", a, c);
	hanoi(n - 1, b, a, c);
}

三柱汉诺塔时间复杂度

这里就直接把手稿放上来了，时间复杂度为O(2^n-1)：在这里插入图片描述
这是一个指数级别的时间复杂度，如果圆盘足够多的话计算量会非常大可能造成栈溢出。

四柱汉诺塔

设有A、B、C、D四根柱子,要把A柱子上的圆盘移动到D柱子上，条件和三根柱子的汉诺塔一样。
大家可以自己在纸上画一画，四柱汉诺塔也可以归纳为以下几个步骤：

1、把n-2个盘子从A移动到B柱子上；
2、把第n-1个柱子从A移动到C上；
3、把第n个柱子从A移动到D上；
4、把第n-1个柱子从C移动到D上；
5、把n-2个盘子从B移动到D柱子上

//递归实现。char a，b,c分别代表A柱、B柱 C柱子
void four_hanoi(int n, char a, char b, char c, char d)
{
	if (1 == n)
	{
		printf("从%c------>%cn", a, d);
		return;
	}
	if (n <= 0)
		return;
	four_hanoi(n - 2, a, c, d, b);
	printf("从%c------>%cn",a, c);
	printf("从%c------>%cn",a,d);
	printf("从%c------>%cn", c, d);
	four_hanoi(n - 2, b, a,c, d); 
}

四柱汉诺塔时间复杂度。

手推时间复杂度如下图，但是这里的结果好像有点不对，把n带入的得不到整数。不过还是可以知道随着柱子越多，时间复杂度趋近于O(n)。
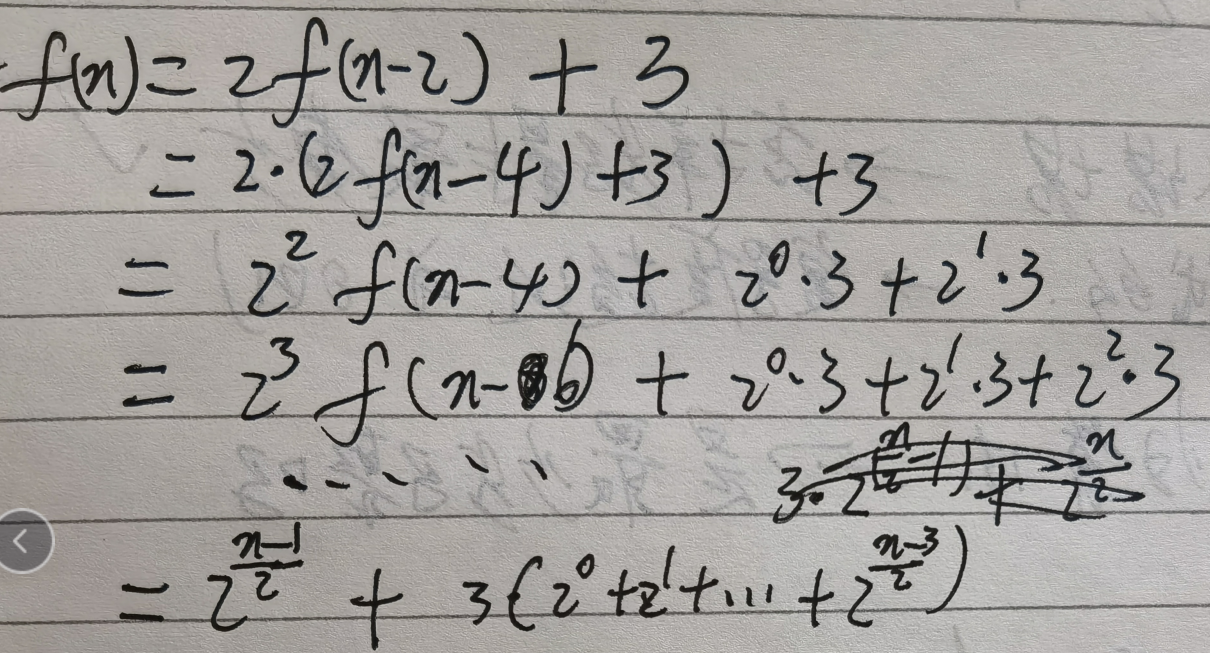
在这里插入图片描述

非递归三柱汉诺塔

总共2个步骤：
1、当盘子数量n为奇数时，最小的盘子按照A—>C---->B的顺序循环移动，例如这一次最小的盘子是从C移动到B的，那么下一次再进行步骤1时，最小的盘子从B移动到A。当盘子数量n为偶数时，最小的盘子按照A—>B---->C的顺序循环移动。
2、没有最小盘子上的两个柱子进行移动。例如A、B上没有最小的盘子，若B柱子上的盘子较小则从B—>A，若A柱子上的盘子较小则从A——>B。
移动时按照上述1、2步骤循环执行，直到游戏结束。
可以用数组实现、也可以用链表实现。
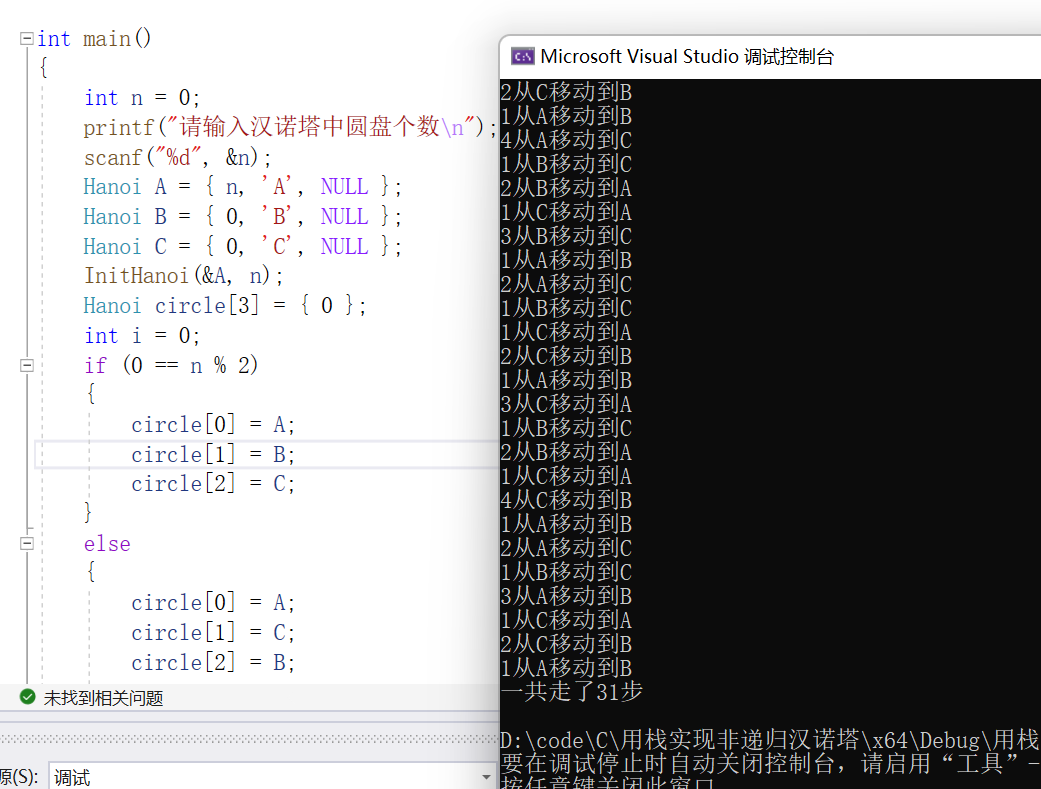
在这里插入图片描述

在我的仓库中用链表实现了非递归汉诺塔：https://gitee.com/wszlight/code/tree/master/%E6%A0%88%E5%AE%9E%E7%8E%B0%E7%9A%84%E9%9D%9E%E9%80%92%E5%BD%92%E6%B1%89%E8%AF%BA%E5%A1%94