青蛙跳台阶及其变种问题原版进阶版变态版非递归方法

54 阅读 0 评论 36 点赞

我是靠谱客的博主孤独画笔，最近开发中收集的这篇文章主要介绍青蛙跳台阶及其变种问题原版进阶版变态版非递归方法，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

青蛙跳台阶是一个非常基础且经典的递归问题，如果你对递归问题还不够熟悉的话，不妨接着看下去，本相信你会有所收获的。

原版

进阶版

变态版

小细节

非递归方法

原版

首先看一下原始问题：

青蛙每次可以跳1-2个台阶
问：该青蛙跳到第n个台阶有多少种跳法？

根据递归的思想大事化小来看，我们虽然不清楚第一步怎么走，但是最后一步的走法却很容易确定，青蛙先想办法跳到第n-1或者第n-2个台阶上，接着再跳一次就能到第n个台阶。即：

f(x) = f(x-1) + f(x - 2)

而如何跳到第n-1个台阶和如何跳到第n-2个台阶又可以套用前面的方法，当然最后肯定会回到怎样跳到第1个台阶和如何跳到第2个台阶，而这两个恰巧我们知道，就可以定义jump(1) == 1,jump(2) == 2。那么这一段写成代码的形式即为：

int jump1(int n)
{
	if (n == 1 || n == 2)
		return n;
	else
		return jump1(n - 1) + jump1(n - 2);
}

进阶版

青蛙每次可以跳1-n个台阶（n > 2）
问：该青蛙跳到第n个台阶有多少种跳法？

这时我们看到青蛙每次跳的次数不确定了，这种情况下如果直接照搬上面的方法显然是行不通的，那我们可不可以先找到相邻两项的关系，然后根据这种关系建立函数呢？

首先看跳到第n个台阶的方法：

其实方法同上面的类似，只不过我们需要写到第n项：

f(n) = f(n-1)+f(n-2)+f(n-3)+…+f(1)

那么跳到第n-1个台阶的函数就为：

f(n-1) =f(n-2)+f(n-3)+f(n-4)…+f(1)

可以发现这两个函数中有大量相同的项，相减后可以得到：

f(n) = 2 * f(n - 1)

那么用函数来表示就是：（这里第二项也包含在第二个式子中了因此不需要单独声明，这里不会出现n<=0的情况因此直接写成n<=1没问题）

int jump2(int n)
{
	if (n <= 1)
		return 1;
	else
		return 2 * jump2(n - 1);
}

变态版

青蛙每次最多可以跳1 - m个台阶
//问：该青蛙跳到第n个台阶有多少种跳法？（m与n的大小不确定）

如果没有前面的问题作铺垫，这道题或许会难倒不少初学者，不过此时不用担心，我们按照前面的思路来入手，首先寻找跳到第n阶和跳到第n-1阶之间的关系：

跳到第n阶：f(n) = f(n - 1) + f(n - 2) + f(n - 3) + …+f(n - m)

当然这时我们会发现一个问题：n比m大的话这个式子没问题，但n比m小的情况似乎有点问题，貌似f(x)的参数会出现负数，其实这个担心是多余的，n比m小实际上同n与m一样大没有区别，比如说青蛙一次最多可以跳10个台阶，而总台阶只有5个，那么所有可能的情况不是就和一次最多跳5个台阶，总共跳5个台阶一样吗？因此只需要分情况讨论就可以解决这个问题了。

第一种情况n<=m，此时函数就同jump2()函数一摸一样了。

第二种情况n>m，同样思路：

f(n) = f(n - 1) + f(n - 2) + f(n - 3) + …+f(n - m)

f(n-1) = f(n - 2)+f(n - 3)+ …+f(n - 1 - (m - 1))+f(n - 1 - m)(注意f(n - 1)中n-1要看成一个整体)

两式相减就得到了f(n)=2 * f(n-1)-f(n-1-m)

两种情况都讨论完了，汇总一下就可以得到我们所需的函数：

int jump3(int m, int n)
{
	//m代表青蛙一次最多可以跳的台阶数
	//n代表青蛙要跳到的台阶数
	if (n <= 1)
		return 1;
	else
		if (m >= n)
			return 2 * jump3(m, n - 1);
		else
			return 2 * jump3(m, n - 1) - jump3(m, n - 1 - m);
}

当然不要忘了我们的第一项是不满足后面递归的条件的，因此单独写出来。

小细节

当然可能有同学认为m = 1, n = 2时最后那个jump3(m, n - 1 - m)就变成了jump3(1, 0)了，而jump3(1, 0)按道理说应该是=0的，显然与我们的n<=1时返回1冲突，那么这又是怎么回事呢？

我们从本质上来看：

比如说青蛙一次跳一个台阶，要跳到第二个台阶就是f(2)=f(1)+f(0)共两种跳法，而f(1)=1,很容易得出f(0)=1。（f(0)的情况其实应该是不存在的，这里是为了满足题意而定义的f(0)=1）

所以说这种边缘情况其实需要单独验证的。

非递归方法

当然这种问题使用递归处理的话会造成大量的重复计算，因此并不推荐使用。这里介绍一下第三题的非递归方法。

对于n<=m的情况：f(n) = 2 * f(n - 1) = 4 * f(n - 2) =…= 2^（n - 1）* f(1).

不过C语言上并没有直接计算某个数的几次方的函数，那么我们就把他写成循环的形式：

int ret = 1;//用来记录结果并返回
int i = 0;
for (i = 1; i < n; i++)//n为总共跳的台阶数
    ret *= 2;
return ret;

而对于n>m的情况：像上面直接递推到第一项的方法是行不通的，我们换个思路：

如果是原版青蛙跳台阶问题我们可以这样做：

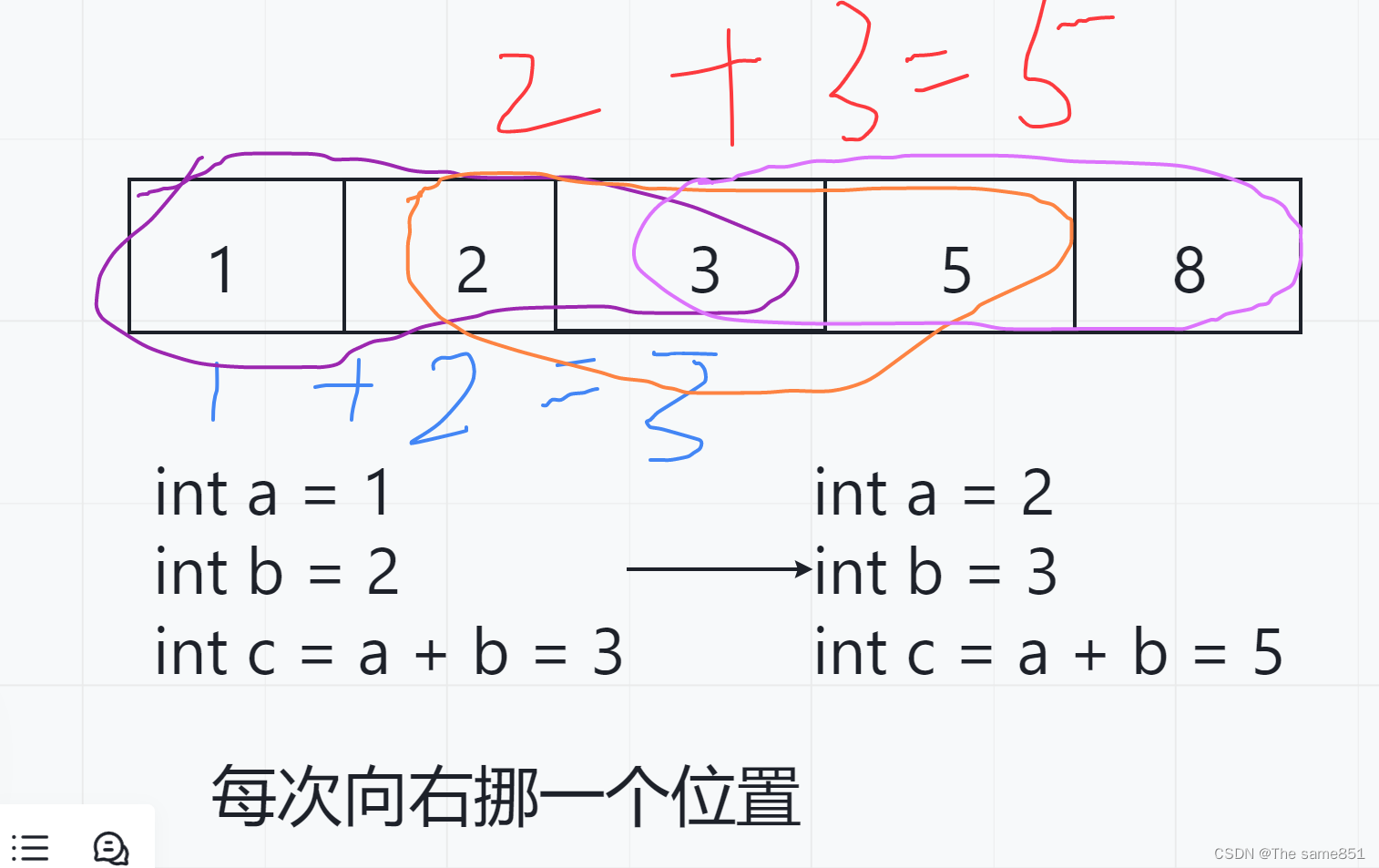
用代码来表示即为：

int jump5(int n)
{
	if (n <= 2)
		return n;
	else
	{
		int ret = 0;
		int n1 = 1;
		int n2 = 2;
		int i = 0;
		for (i = 3; i <= n; i++)
		{
			ret = n1 + n2;
			n1 = n2;
			n2 = ret;
		}
		return ret;
	}
}

既然每次跳1-2个台阶可以这样做，那么每次跳1-m个台阶也可以仿照这来写：

首先跳到m个台阶之前都可以套用f(n)=2 * f(n-1)（这里的n即为跳到的台阶数，因此m是大于这里的n的），接着使用循环把这m项加起来得到第m+1项，同时把这m+1项都存到数组中去，而在后续再将每个元素下标+1即得到新的元素（这里原理同原版非递归问题），这里m<n的情况就大致解决了。

那么再结合之前讨论的m>=n的情况，合在一起即为所求函数：

int jump4(int m, int n)
{
	int i = 0;
	int ret = 1;
	if (n <= 1)
		return 1;
	else
		if (m >= n)
		{
			for (i = 1; i < n; i++)
				ret *= 2;
			return ret;
		}
		else
		{
			int arr[20] = { 0 };//这里数组的大小只要比m打就可以
			int i = 0;
			int j = 0;
			int tmp = 1;//第一项的值为1
			int ret = 0;
			for (i = 0; i < m; i++)
			{
				arr[i] = tmp;
				tmp *= 2;//得到第一项到第m项的值并存在数组中
			}
			for (i = m; i < n; i++)
			{
				ret = 0;
				for (j = 0; j < m; j++)
				{
					ret += arr[j];
				}
				arr[j] = ret;
				//出循环得到的ret即为第m+1项的值
				for (j = 0; j < m; j++)
				{
					arr[j] = arr[j + 1];//将每个元素向后移动一位
				}
			}
			return arr[j];
		}
}

这种方法的话思路确实挺难想到，不过既然它是青蛙跳台阶的变态问题，那就和原版会有一定的相同之处，在思考时多想想关联，在很多时候也会有所启发。当然，有的时候递归确实很容易想到，虽然效率可能较低，但若是实在没有办法，使用递归也无妨。