卡特兰数+卢卡斯定理+组合数

65 阅读 0 评论 43 点赞

我是靠谱客的博主矮小大碗，最近开发中收集的这篇文章主要介绍卡特兰数+卢卡斯定理+组合数，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

既然写到这里了就先来写一下卡特兰数吧；

卡特兰数有四个公式，但我们要分析每个公式的用处。

公式一

递归公式

h(0) = h(1) = 1

h(n) = h(0) * h(n-1) + h(1) * h(n-2) + … + h(n-1) * h(0) (n>=2)

如果我们用这个公式显然我们要使用递归算法，那么数据一大就在时空上很麻烦

公式二

递推公式

h(n) = h(n-1) * (4 * n - 2) / ( n + 1 )

这个公式应用递推，但是对于大数据有点鸡肋

我们注意到大数据的时候h(n)会很大，这时候题目一般会让你对某素数取模（~~当然你可以打高精度~~ ）

但你在取模过程中难保一个h(n)%mod=0

那么根据公式下面所有的数都会等于0，于是你就愉快的WA了

##公式三

组合数公式1

h(n) = C( 2n , n ) / ( n + 1 ) ( n=0,1,2,… )

卡特兰数可以与组合数联系起来，得到上面的公式

而组合数就是一个杨辉三角，可以递推得到但我们发现对于大数据你要取模，而对于除法你是没办法用膜的性质的（~~当然你可以应用逆元~~
），所以造成了麻烦

##公式四

组合数公式2

h(n)= c(2n,n) - c(2n,n-1) (n=0,1,2,…)

与组合数公式1不同这个是两个组合数的减法

手推了三和四等价关系

在这里插入图片描述

组合数大佬博客

一些有关的题目

1120 机器人走方格 V3（卡特兰数+卢卡斯定理）

题意：就是给你一个N*N的方格，从左上到右下画一条线。一个机器人从左上走到右下，只能向右或向下走。并要求只能在这条线的上面或下面走，不能穿越这条线，有多少种不同的走法？由于方法数量可能很大，只需要输出Mod 10007的结果。

题解：这题实际上是一个卡特兰数，以我最近看了几篇卡特兰数的讲解，对于这个就是栈的一个模型，我们向右为入栈，向上为出栈，本质就是n个数出栈次序的问题，这个题很有意思的是，与大多数博客讲课类型不同，很多博客讲的是从边跑，而这个题是在一个小矩形跑，当然如果数据小我们也可以dp
这个题作为板子很好，代码很精简而是好看，这个上传一个大佬的知乎，关于卢卡斯定理；
卢卡斯定理推导

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define fio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define mse(a,b) memset(a,b,sizeof a)
#define pb push_back
using namespace std;
const int mod=1e9+7;
const int maxx=1e6+10;
using namespace std;
const long double PI = 3.14159265358979323846;
//inline int read(){ int x=0,f=1; char ch=getchar(); while (!isdigit(ch)) { if (ch=='-') f=-1; ch=getchar(); } while (isdigit(ch)) { x=x*10+ch-48;  ch=getchar();  } return x*f;}
//     ll cc = ((1ll << 62) - 1 + (1ll << 62));
ll ans[maxx];
ll qpow(ll a,ll b,ll p)
{
    ll sum=1;
    while(b)
    {
        if(b&1)
        sum=sum*a%p;
        a=a*a%p;
        b>>=1;
    }
    return sum;
}
ll C(ll a,ll b,ll p)
{
    return a < b ? 0 : (ans[a]*qpow(ans[b]*ans[a-b]%p,p-2,p)%p)%p;
}
ll lucas(ll n,ll m,ll p)
{
    return m==0?1%p:lucas(n/p,m/p,p)*C(n%p,m%p,p)%p;
}
signed main()
{
   // cout<<qpow(2,10,1010101)<<endl;
    ll n;
    ans[0]=1;
    for(int i=1; i<=10007; i++)
        ans[i]=ans[i-1]*i%10007;
    cin>>n;
    n--;
    ll pp=lucas(2*n,n,10007)%10007;
    ll cc=pp*qpow(n+1,10005,10007);
    //ll cc=lucas(n<<1,n-1,10007);
    cout<<2*cc%10007<<endl;
    return 0;
}

有一个无限大的矩形，初始时你在左上角（即第一行第一列），每次你都可以选择一个右下方格子，并瞬移过去（如从下图中的红色格子能直接瞬移到蓝色格子），求到第n行第m列的格子有几种方案，答案对1000000007取模。
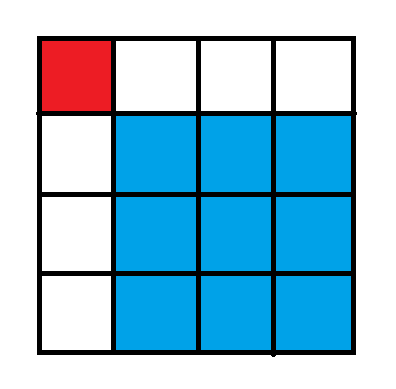
在这里插入图片描述
送你过去
题解:
根据图片我们可以很清晰的看到要想选择之后的方块并且最后可以到底右下角,那么必然只有选择2–n-1行,2–m-1列的方块,那么就可以很明显的看到每一行和每一列都只可以选择共同的一个,然后继续往右下选择,那么就枚举每行每列选几个就可以推出一个公式:
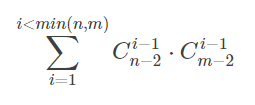
在这里插入图片描述

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include<bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define fio ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
#define mse(a,b) memset(a,b,sizeof a)
#define pb push_back
using namespace std;
const int mod=1e9+7;
const int maxx=1e6+10;
using namespace std;
const long double PI = 3.14159265358979323846;
//inline int read(){ int x=0,f=1; char ch=getchar(); while (!isdigit(ch)) { if (ch=='-') f=-1; ch=getchar(); } while (isdigit(ch)) { x=x*10+ch-48;  ch=getchar();  } return x*f;}
//     ll cc = ((1ll << 62) - 1 + (1ll << 62));
ll fa[maxx];
ll qpow(ll a,ll b){
   ll sum=1;
   while(b){
    if(b&1) sum=sum*a%mod;
    a=a*a%mod;
    b>>=1;
   }
   return sum;
}
signed main()
{
    fa[0]=1;
   for(int i=1;i<=100000;i++) fa[i]=fa[i-1]*i%mod;
   ll n,m;
   cin>>n>>m;
   ll sum=0;
   for(int i=0;i<=min(n-2,m-2);i++)
   {
       sum+=fa[n-2]*qpow(fa[i]*fa[n-2-i]%mod,mod-2)%mod*fa[m-2]%mod*qpow(fa[i]*fa[m-2-i]%mod,mod-2)%mod;
       sum%=mod;

   }
   cout<<sum<<endl;
    return 0;
}