求组合数有很多种题型，我们需要根据输入的数据的范围来选哪种方式，具体的方式有如下几种：
主要是询问次数和数据大小的不同，对应了不同的解法
此外，另有高精度组合数和卡特兰数两种特例
星号表示本题的思想。

1. 题目

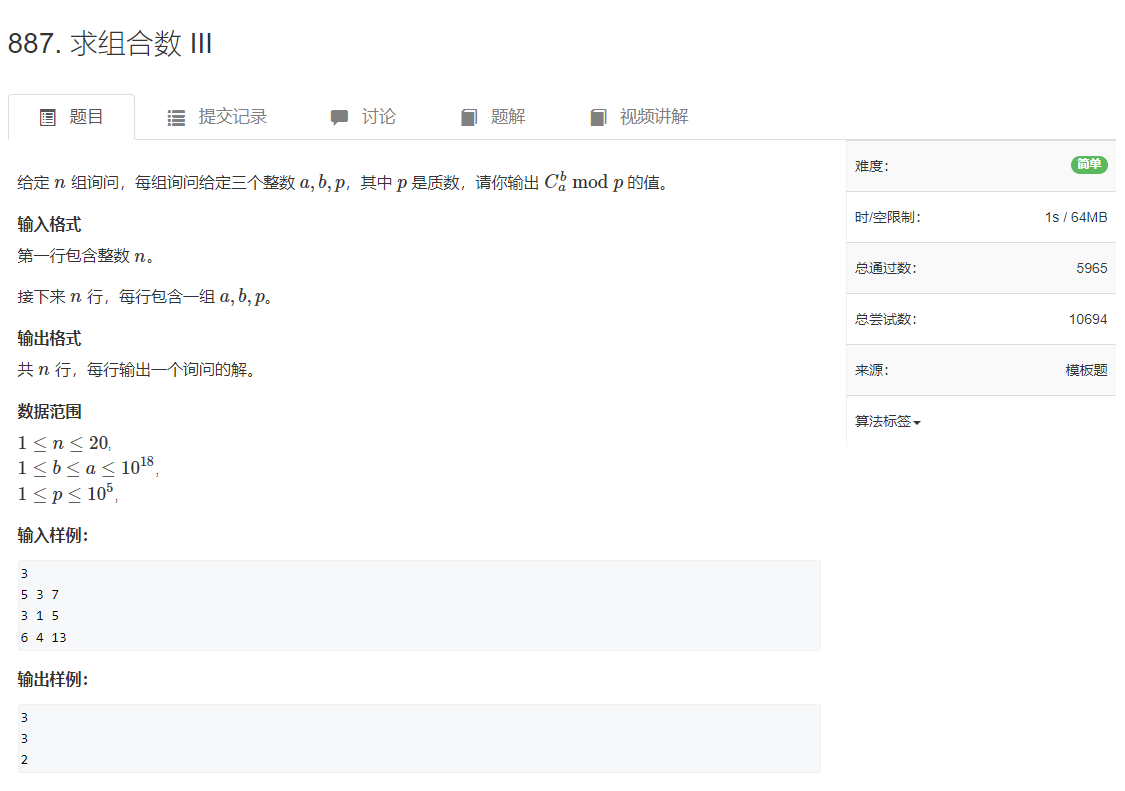
2. 读题（需要重点注意的东西）

思路：

首先，要知道组合数是什么？公式是什么？
一般地，从a个不同的元素中，任取b（b≤a）个元素为一组，叫作从aa个不同元素中取出b个元素的一个组合，这个组合一共有多少组？
普通公式如下：

由于本题的数据超级超级大（1e18），因此使用卢卡斯定理解决：

卢卡斯定理

3. 解法

---------------------------------------------------解法---------------------------------------------------

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

// 快速幂求a的k次方模p
int qmi(int a, int k, int p)
{
    int res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}

//由定义计算组合数
int C(int a, int b, int p)
{
    if (b > a) return 0; // 如果b > a，组合数为0

    int res = 1;
    // 由定义计算组合数
    for (int i = 1, j = a; i <= b; i ++, j -- )
    {
    	// 乘j
        res = (LL)res * j % p;
        // 除i，注意：除i等同于乘i的逆元
        res = (LL)res * qmi(i, p - 2, p) % p;
    }
    return res;
}

// 卢卡斯定理
int lucas(LL a, LL b, int p)
{
	// 如果a和b都小于p，从定义来计算组合数C
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}


int main()
{
    int n;
    cin >> n;

    while (n -- )
    {
        LL a, b;
        int p;
        cin >> a >> b >> p;
        // 卢卡斯定理求组合数
        cout << lucas(a, b, p) << endl;
    }

    return 0;
}

1、C函数的作用是什么？
C函数是从如下定义计算组合数

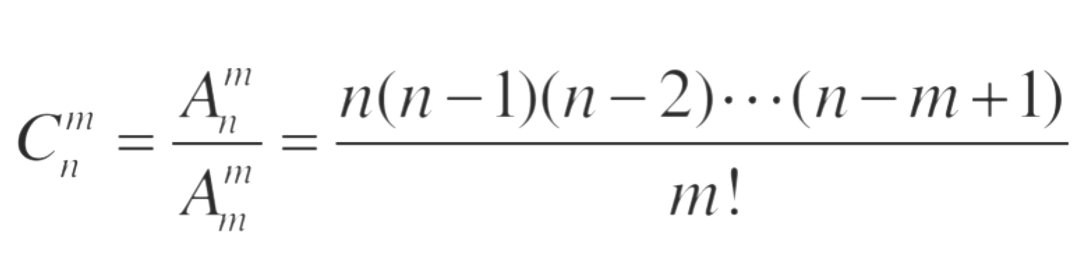
2、为什么实现卢卡斯定理的代码是这样的？

// 卢卡斯定理
int lucas(LL a, LL b, int p)
{
	// 如果a和b都小于p，从定义来计算组合数C
    if (a < p && b < p) return C(a, b, p);
    return (LL)C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;
}

此处只给出公式：

4. 可能有帮助的前置习题

• [AcWing]876. 快速幂求逆元（C++实现）快速幂求逆元模板题
• [AcWing] 886. 求组合数 II（C++实现）求组合数第二种题型模板题

5. 所用到的数据结构与算法思想

• 组合数
• 快速幂
• 卢卡斯定理

6. 总结

求组合数第三种题型（卢卡斯定理）的模板题，理解思路并背下代码。

最后

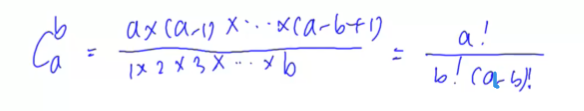
以上就是顺心小丸子为你收集整理的[AcWing] 887. 求组合数 III（C++实现）求组合数第三种题型（卢卡斯定理）模板题1. 题目2. 读题（需要重点注意的东西）3. 解法4. 可能有帮助的前置习题5. 所用到的数据结构与算法思想6. 总结的全部内容，希望文章能够帮你解决[AcWing] 887. 求组合数 III（C++实现）求组合数第三种题型（卢卡斯定理）模板题1. 题目2. 读题（需要重点注意的东西）3. 解法4. 可能有帮助的前置习题5. 所用到的数据结构与算法思想6. 总结所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。