1. 题目

2. 转述
原题目要求可以简化为:
对于二维对流方程:
∂u/∂t+∂u/∂x+∂u/∂y=0
u(x,y,0)={█(1,when-4≤x≤4,-4≤y≤4@0,other)┤
取计算范围为 -16≤x≤16,-16≤y≤16,Δx=Δy=1,Δt/Δx=Δt/Δy=0.5,1,2,t>0,使用 A,B,C格式与蛙跳格式计算90个时间步长,制作 u-x-y 图随时间的动画,依此分析四种格式对于二维对流方程的稳定性。

3. 分析
之前分析一维对流方程的代码
https://blog.csdn.net/PriceCheap/article/details/124172427
基本可以照抄的
只不过现在看还是有可以修改的地方
3.1 MeshGrid
之前求 X F 向量是封到一个函数里
旧代码 1
% 多个 dxdt 情况对比
for i = 1:1:size(dxdt,2)
Delta_t = Delta_x/dxdt(i);
[F,X,T] = PreDifferenceProcess(x_border,x_initialBorder,Delta_x,Delta_t,@InitialCondition);
旧代码 2
function [F,X,T] = PreDifferenceProcess(x_border,x_initialBorder,Delta_x,Delta_t,InitialCondition)
% 求差分格式之前需要的前处理
% t 的最大步数
% 由 x_initialBorder 与 x_border 之间的空隙决定
n_border = (x_border - x_initialBorder)/Delta_x + 1;
% x 的向量
X = -x_border : Delta_x : x_border;
% t 的向量
T = 0 : Delta_t : n_border * Delta_t;
% 流场物理量矩阵初始化
F = zeros(size(X,2),size(T,2));
% 初始条件
for i = 1:1:size(F,1)
F(i,1) = InitialCondition(X(i));
end
end
现在想想是没有必要的,直接 MeshGrid 就好了
这样直接用 X Y 矩阵也挺好
新代码
% 求 T 向量
t = differenceBorder(5):dt:differenceBorder(6);
% 多个 dxdt 情况对比
for i = 1:1:max(size(dtdx))
% 求步长
dx = dt/dtdx(i);
dy = dt/dtdy(i);
% 求 X 和 Y 向量
x = differenceBorder(1):dx:differenceBorder(2);
y = differenceBorder(3):dy:differenceBorder(4);
% 求 X 和 Y 矩阵
% X 矩阵每一行都是 X 向量
% Y 矩阵每一列都是 Y 向量
% 和 XOY 坐标系的直觉相配
[X,Y] = meshgrid(x,y);
3.2 ParasValidater
闲得无聊写了一个验证输入的函数……万一有人真的想用我的函数呢x
类似这样
% 验证 alpha, beta 是否合法
if alpha == 0
error("alpha 需为非零!");
end
if beta == 0
error("beta 需为非零!");
end
% 验证 differenceBorder 是否合法
if min(size(differenceBorder)) ~= 1 || length(size(differenceBorder)) ~= 2
error("differenceBorder 需为一维向量!");
end
if max(size(differenceBorder)) ~= 6
error("differenceBorder 需有六个元素!");
end
if differenceBorder(1) > differenceBorder(2)
error("differenceBorder 中 X 的下界需要小于 X 的上界!");
end
if differenceBorder(3) > differenceBorder(4)
error("differenceBorder 中 Y 的下界需要小于 Y 的上界!");
end
if differenceBorder(5) > differenceBorder(6)
error("differenceBorder 中 T 的下界需要小于 T 的上界!");
end
3.3 TryGetElement
差分格式要取的点可能超出边界
我之前的做法是生硬地分情况讨论
旧代码
if i<2
tmp2 = 0;
else
tmp2 = F(i-1,n);
end
if i>size(F,1)-1
tmp1 = 0;
else
tmp1 = F(i+1,n);
end
现在我统一使用一个函数来判断是否需要取 0
新代码 2
for x = 1:1:size(Zeta,1)
for y = 1:1:size(Zeta,2)
% 基点
base = TryGetElement(Zeta,x,y);
% 基点 x 正方向一步
right = TryGetElement(Zeta,x+1,y);
% 基点 x 负方向一步
left = TryGetElement(Zeta,x-1,y);
% 基点 y 正方向一步
up = TryGetElement(Zeta,x,y+1);
% 基点 y 负方向一步
down = TryGetElement(Zeta,x,y-1);
新代码 2
function [element] = TryGetElement(Array,row,col)
% 超出边界的可以取 0 而不损失精度
if row < 1 || row > size(Array,1)
element = 0;
return;
end
if col < 1 || col > size(Array,2)
element = 0;
return;
end
element = Array(row,col);
end
3.4 Zeta(x,y)
之前我是把待求函数的值和时间放在一起了,所以就显得很……乱吧
这下我把这两个分离开了,所以我可以写 Zeta(x,y) 而不是 Zeta(x,y,n+1)
旧代码 A 格式
function [F] = DifferenceFormat_A(F,a,Delta_x,Delta_t)
% A 格式
% (F(i,n+1)-F(i,n))/Delta_t + a*(F(i+1,n)-F(i-1,n))/(2*Delta_x) = 0
% => F(i,n+1) = F(i,n) -a/2*Delta_t/Delta_x*(F(i+1,n)-F(i-1,n))
for n = 1:1:size(F,2)-1
for i = 1:1:size(F,1)
% 超出边界的可以取 0 而不损失精度
if i<2
tmp2 = 0;
else
tmp2 = F(i-1,n);
end
if i>size(F,1)-1
tmp1 = 0;
else
tmp1 = F(i+1,n);
end
F(i,n+1) = F(i,n) - a/2*Delta_t/Delta_x*(tmp1-tmp2);
end
end
end
新代码 A 格式
function [Zeta_New] = DifferenceFormat_A_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 A 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
Zeta_New = zeros(size(Zeta));
for x = 1:1:size(Zeta,1)
for y = 1:1:size(Zeta,2)
% 基点
base = TryGetElement(Zeta,x,y);
% 基点 x 正方向一步
right = TryGetElement(Zeta,x+1,y);
% 基点 x 负方向一步
left = TryGetElement(Zeta,x-1,y);
% 基点 y 正方向一步
up = TryGetElement(Zeta,x,y+1);
% 基点 y 负方向一步
down = TryGetElement(Zeta,x,y-1);
Zeta_New(x,y) = base - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
end
end
3.5 dtdx dtdy
之前我在总的差分函数里面是传入一个 dtdx 的向量,然后我函数里面对这个向量 for
但是现在我有了打印 png 的需求,就感觉,什么地方都要用到 dtdx 的计数器 i 来区分情况就很烦
所以感觉把这个总的函数做成只处理 dtdx dtdy 为常数的就好了,这才是简洁的
在外面多次调用这个函数
旧代码 ODCE_DifferenceProcess
% 多个 dxdt 情况对比
for i = 1:1:size(dxdt,2)
Delta_t = Delta_x/dxdt(i);
[F] = DifferenceFormat(F,a,Delta_x,Delta_t);
新代码 ConvectionEqDifferenceMethod_2D
Zeta = DifferenceFormatFun(Zeta,alpha,beta,dtdx,dtdy);
旧代码 外部调用函数
ODCE_DifferenceProcess(@DifferenceFormat_A,'A',@InitialCondition,a,x_border,x_initialBorder,Delta_x,dxdt);
新代码 外部调用函数
for i = 1:1:max(size(dtdx))
ConvectionEqDifferenceMethod_2D(@DifferenceFormat_A_2D,'A', ...
alpha,beta,differenceBorder, ...
@InitializationFun,initializationBorder, ...
dt,dtdx(i),dtdy(i))
end
3.6 moive
创建动画的话,我本来还想使用 print 输出多个 png,然后再用 ps 拼成一个 gif 的
之后发现了 movie 可以直接播放动画,那就不用 gif 这么麻烦了
直接在每一次画图的时候先 drawnow 然后 getframe 最后播放就好了
旧代码 ODCE_DifferenceProcess
% 多个 dxdt 情况, 多个缩放情况对比
for i = 1:1:size(dxdt,2)
figure();
for j = 1:1:size(scale,2)
subplot(size(scale,2),1,j);
mesh(T_scaled,X_scaled,F_scaled,'FaceColor','flat');
新代码 ConvectionEqDifferenceMethod_2D
% 迭代时间步
for i = 1:1:max(size(t))
% ---画图---
% 平面着色
mesh(X,Y,Zeta,'FaceColor','flat');
% 捕获影片帧
drawnow;
Moive(i) = getframe;
3.7 InRange
题目中给的初始化函数可以简化为一个是否在范围内的函数
Matlab 没有提供这个函数我有点奇怪
或许是我查询的关键字错了才没有查到
function [IsInRange] = InRange(element,lower,upper)
% 在范围内返回 1
% 不在范围内返回 0
if element > lower && element < upper
IsInRange = 1;
return;
end
IsInRange = 0;
end
3.8 No Searching Loop
我在别的地方看到一个原则就是
推荐使用矩阵矢量化运算,而不是多重循环遍历矩阵
因为矩阵是 Matalb 的一个结构体,对矢量运算有优化
但是多重循环遍历矩阵每个元素那就一定是 o(nm) 的时间
我定义了一个 InRange 来判断一个函数是否是在一个给定的范围内
如果直接用的话,那么如果输入一个矩阵,这个矩阵会和一个数比较,比较不了
测试代码 1
InitializationFun = @(X,Y) InRange(X,initializationBorder(1),initializationBorder(2)).*InRange(Y,initializationBorder(3),initializationBorder(4));
我本来想用 bsxfun 来实现不用循环,因为它的功能是对两个矩阵的每一组对应元素都执行给定函数嘛
结果我发现即使如此,bsxfun 传给输入函数的变量依然是矩阵而不是元素
测试代码 2
InInitializationRange = @(x,y) InRange(x,initializationBorder(1),initializationBorder(2)).*InRange(y,initializationBorder(3),initializationBorder(4));
InitializationFun = @(X,Y) bsxfun(InInitializationRange,X,Y);
因此我的 InRange 必须要改成能够处理一个矩阵的形式
也就是说我要默认我的输入就是矩阵
所以我之后写成了
新代码 InRange
function [X_Ans] = InRange(X,lower,upper)
% 在范围内返回 1
% 不在范围内返回 0
% 坐标系平移,使得区间原点为坐标系原点
mid = lower + (upper - lower)/2;
X_Ans = X - mid;
% 取每一个点到原点的长度
halfLength = upper - mid;
X_Ans = abs(X_Ans);
% 取每一个点到原点的长度与区间半长之间的关系
% 点在区间内,则值为 -1
% 点在边界,则值为 0
% 点在区间外,则值为 1
X_Ans = sign(X_Ans - halfLength);
% 每一个点减 1,使得点在区间内和点在边界这两种情况 -2 -1 都为负数,和点在区间外的情况 0 分离开
X_Ans = X_Ans - 1;
% 取每一个点在区间内外的关系
% 点在区间内或者在区间边界,则值为 -1
% 点在区间外,则值为 0
X_Ans = sign(X_Ans);
% 取每一个点在区间内外的关系
% 点在区间内或者在区间边界,则值为 1
% 点在区间外,则值为 0
X_Ans = abs(X_Ans);
end
3.9 MatrixTranslation
我原来的差分格式也是按照循环写的
也可以根据这个不使用循环的思路修改
旧代码 差分格式
function [element] = TryGetElement(Array,row,col)
% 超出边界的可以取 0 而不损失精度
if row < 1 || row > size(Array,1)
element = 0;
return;
end
if col < 1 || col > size(Array,2)
element = 0;
return;
end
element = Array(row,col);
end
function [Zeta_New] = DifferenceFormat_A_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 A 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
Zeta_New = zeros(size(Zeta));
for x = 1:1:size(Zeta,1)
for y = 1:1:size(Zeta,2)
% 基点
base = Zeta(x,y);
% 基点 x 正方向一步
right = TryGetElement(Zeta,x+1,y);
% 基点 x 负方向一步
left = TryGetElement(Zeta,x-1,y);
% 基点 y 正方向一步
up = TryGetElement(Zeta,x,y+1);
% 基点 y 负方向一步
down = TryGetElement(Zeta,x,y-1);
Zeta_New(x,y) = base - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
end
end
function [Zeta_New] = DifferenceFormat_B_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 B 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))
Zeta_New = zeros(size(Zeta));
for x = 1:1:size(Zeta,1)
for y = 1:1:size(Zeta,2)
% 基点
base = Zeta(x,y);
% 基点 x 正方向一步
right = TryGetElement(Zeta,x+1,y);
% 基点 y 正方向一步
up = TryGetElement(Zeta,x,y+1);
Zeta_New(x,y) = base - alpha/2*dtdx*(right-base) - beta/2*dtdy*(up-base);
end
end
end
function [Zeta_New] = DifferenceFormat_C_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 C 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi,n)-Zeta(xi,yi-1,n))
Zeta_New = zeros(size(Zeta));
for x = 1:1:size(Zeta,1)
for y = 1:1:size(Zeta,2)
% 基点
base = Zeta(x,y);
% 基点 x 负方向一步
left = TryGetElement(Zeta,x-1,y);
% 基点 y 负方向一步
down = TryGetElement(Zeta,x,y-1);
Zeta_New(x,y) = base - alpha/2*dtdx*(base-left) - beta/2*dtdy*(base-down);
end
end
end
function [Zeta_New] = DifferenceFormat_LeapFrog_2D(Zeta,Zeta_Old,alpha,beta,dtdx,dtdy)
% 二维对流方程 蛙跳 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n-1))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n-1) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
Zeta_New = zeros(size(Zeta));
for x = 1:1:size(Zeta,1)
for y = 1:1:size(Zeta,2)
% 基点
base_old = Zeta_Old(x,y);
% 基点 x 正方向一步
right = TryGetElement(Zeta,x+1,y);
% 基点 x 负方向一步
left = TryGetElement(Zeta,x-1,y);
% 基点 y 正方向一步
up = TryGetElement(Zeta,x,y+1);
% 基点 y 负方向一步
down = TryGetElement(Zeta,x,y-1);
Zeta_New(x,y) = base_old - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
end
end
以前在循环体里面就是对矩阵中的每一个元素都做几次偏移
我现在新建一个 MatrixTranslation 函数来做这件事情,我使得整个矩阵都向某个方向偏移,然后直接用矩阵算出来物理量矩阵下一时间步的值
新代码 MatrixTranslation
function [Zeta_New] = MatrixTranslation(Zeta,xstep,ystep)
% 将矩阵在 x 方向上平移 xstep 个单位,在 y 方向上平移 ystep 个单位
% 这个平移不是仿射变换,只是元素相对位置的平移
% 空余的位置用 0 补充
% 移动距离超出矩阵长度的会得到全零
if abs(xstep) >= size(Zeta,1) || abs(ystep) >= size(Zeta,2)
Zeta_New = zeros(size(Zeta));
return;
end
Zeta_New = Zeta;
if xstep > 0
Zeta_New = Zeta_New(:,1:size(Zeta,2)-xstep);
Zeta_New = [zeros(size(Zeta,1),xstep) Zeta_New];
end
if xstep < 0
Zeta_New = Zeta_New(:,1-xstep:size(Zeta,2));
Zeta_New = [Zeta_New zeros(size(Zeta,1),-xstep)];
end
if ystep > 0
Zeta_New = Zeta_New(1:size(Zeta,1)-ystep,:);
Zeta_New = [Zeta_New;zeros(ystep,size(Zeta,2))];
end
if ystep < 0
Zeta_New = Zeta_New(1-ystep:size(Zeta,1),:);
Zeta_New = [zeros(-ystep,size(Zeta,2));Zeta_New];
end
end
由此得到的新的差分格式
function [Zeta_New] = DifferenceFormat_A_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 A 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
right = MatrixTranslation(Zeta,1,0);
left = MatrixTranslation(Zeta,-1,0);
up = MatrixTranslation(Zeta,1,0);
down = MatrixTranslation(Zeta,-1,0);
Zeta_New = Zeta - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
好吧,感觉并没有提速多少
可能是因为传递矩阵的时候还要拷贝矩阵的问题?
结果对比来看
使用 MatrixTranslation 的 DifferenceFormat_A_2D
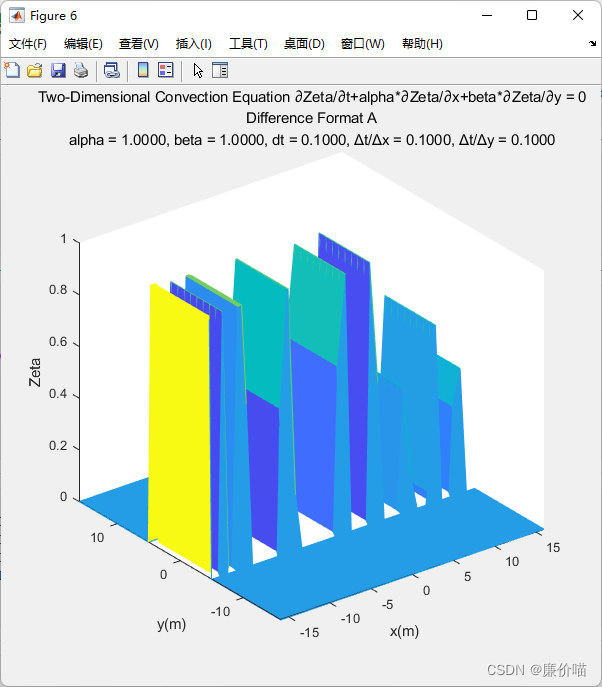
使用 TryGetElement 的 DifferenceFormat_A_2D
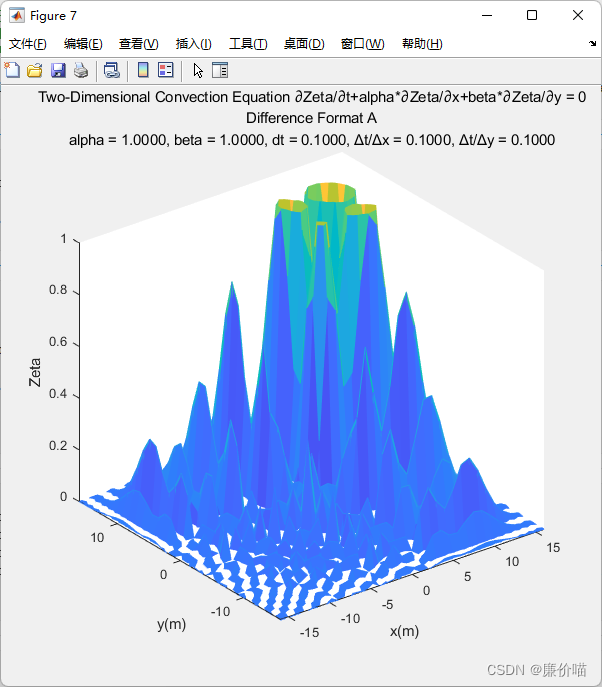
使用 MatrixTranslation 的 DifferenceFormat_A_2D 完全错了
太怪了
测试一下应该是我的 MatrixTranslation 写错了
测试代码
A=[1 2 3;4 5 6;7 8 9];
disp(A);
disp(MatrixTranslation(A,1,0));
disp(MatrixTranslation(A,-1,0));
disp(MatrixTranslation(A,0,1));
disp(MatrixTranslation(A,0,-1));
运行结果
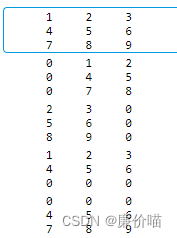
好吧确实错了……
正确代码 MatrixTranslation
function [Zeta_New] = MatrixTranslation(Zeta,xstep,ystep)
% 将矩阵在 x 方向上平移 xstep 个单位,在 y 方向上平移 ystep 个单位
% 这个平移不是仿射变换,只是元素相对位置的平移
% 空余的位置用 0 补充
% 移动距离超出矩阵长度的会得到全零
if abs(xstep) >= size(Zeta,1) || abs(ystep) >= size(Zeta,2)
Zeta_New = zeros(size(Zeta));
return;
end
Zeta_New = Zeta;
if xstep > 0
Zeta_New = Zeta_New(:,1:size(Zeta,2)-xstep);
Zeta_New = [zeros(size(Zeta,1),xstep) Zeta_New];
end
if xstep < 0
Zeta_New = Zeta_New(:,1-xstep:size(Zeta,2));
Zeta_New = [Zeta_New zeros(size(Zeta,1),-xstep)];
end
if ystep > 0
Zeta_New = Zeta_New(1+ystep:size(Zeta,1),:);
Zeta_New = [Zeta_New;zeros(ystep,size(Zeta,2))];
end
if ystep < 0
Zeta_New = Zeta_New(1:size(Zeta,1)+ystep,:);
Zeta_New = [zeros(-ystep,size(Zeta,2));Zeta_New];
end
end
运行结果
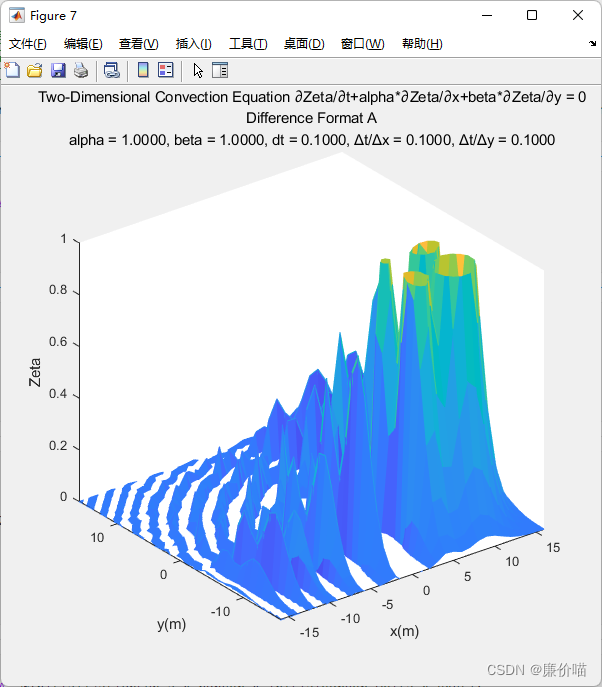
正常了正常了
再加一点细节
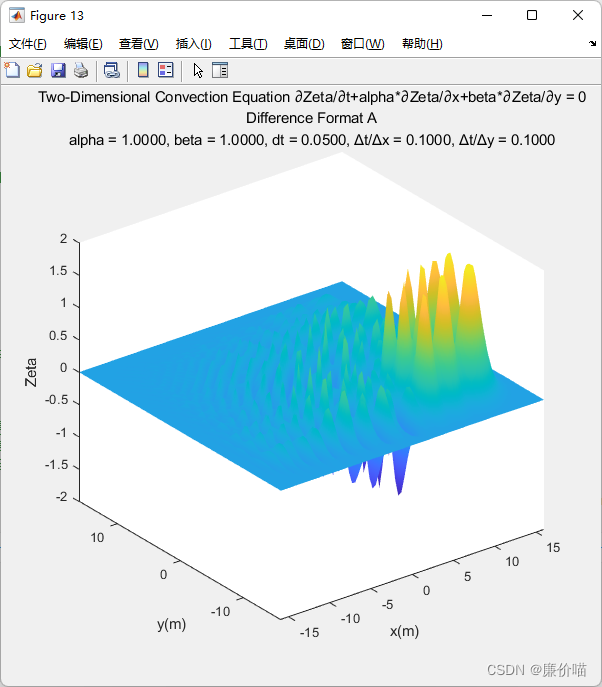
综上,新的更简洁的差分函数为
function [Zeta_New] = DifferenceFormat_A_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 A 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
right = MatrixTranslation(Zeta,-1,0);
left = MatrixTranslation(Zeta,1,0);
up = MatrixTranslation(Zeta,0,-1);
down = MatrixTranslation(Zeta,0,1);
Zeta_New = Zeta - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
function [Zeta_New] = DifferenceFormat_B_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 B 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))
right = MatrixTranslation(Zeta,-1,0);
up = MatrixTranslation(Zeta,0,-1);
Zeta_New = Zeta - alpha/2*dtdx*(right-Zeta) - beta/2*dtdy*(up-Zeta);
end
function [Zeta_New] = DifferenceFormat_C_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 C 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi,n)-Zeta(xi,yi-1,n))
left = MatrixTranslation(Zeta,1,0);
down = MatrixTranslation(Zeta,0,1);
Zeta_New = Zeta - alpha/2*dtdx*(Zeta-left) - beta/2*dtdy*(Zeta-down);
end
function [Zeta_New] = DifferenceFormat_LeapFrog_2D(Zeta,Zeta_Old,alpha,beta,dtdx,dtdy)
% 二维对流方程 蛙跳 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n-1))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n-1) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
right = MatrixTranslation(Zeta,-1,0);
left = MatrixTranslation(Zeta,1,0);
up = MatrixTranslation(Zeta,0,-1);
down = MatrixTranslation(Zeta,0,1);
Zeta_New = Zeta_Old - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
3.10 LeapFrog
如果是蛙跳模式,就需要处理多个时间步的物理量矩阵
如果处在第 1 个时间步,也就是初始状态时
那么蛙跳格式中的 (Zeta(xi,yi,n+1)-Zeta(xi,yi,n-1))/dt 中的
Zeta(xi,yi,n-1) 不能赋 0 这会和初值产生梯度很大的冲突导致强烈的震荡
也不能令 Zeta_Old = Zeta;
也就是不能令蛙跳格式在第 1 个时间步取到的第 0 个时间步的物理量矩阵就是第 1 个时间步的矩阵
这样的话蛙跳格式就会退化成 A 格式
因此蛙跳格式只适合在已知上一时间步的物理量矩阵时使用
也就是要在第 2 个时间步或者更后的时间上使用
% 如果是蛙跳模式,就需要处理多个时间步的物理量矩阵
if FormatName == "LeapFrog"
% 如果处在第 1 个时间步,也就是初始状态时
% 那么蛙跳格式中的 (Zeta(xi,yi,n+1)-Zeta(xi,yi,n-1))/dt 中的
% Zeta(xi,yi,n-1) 不能赋 0 这会和初值产生梯度很大的冲突导致强烈的震荡
% 也不能令 Zeta_Old = Zeta;
% 也就是不能令蛙跳格式在第 1 个时间步取到的第 0 个时间步的物理量矩阵就是第 1 个时间步的矩阵
% 这样的话蛙跳格式就会退化成 A 格式
% 因此蛙跳格式只适合在已知上一时间步的物理量矩阵时使用
% 也就是要在第 2 个时间步或者更后的时间上使用
if i == 1
Zeta_New = DifferenceFormat_A_2D(Zeta,alpha,beta,dt/dx,dt/dy);
else
Zeta_New = DifferenceFormatFun(Zeta,Zeta_Old,alpha,beta,dt/dx,dt/dy);
end
Zeta_Old = Zeta;
Zeta = Zeta_New;
实验得到第 1 个时间步使用 A 格式或者 C 格式得到的结果是相似的
3.11 报告正文





4. 结果
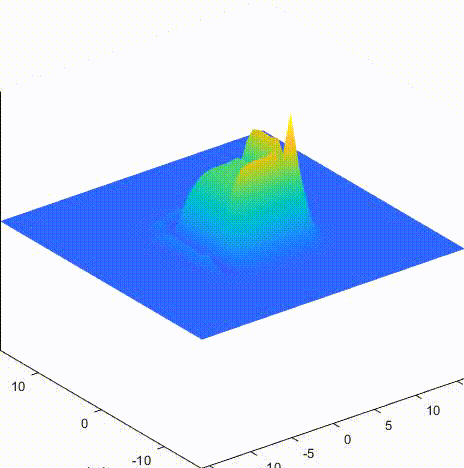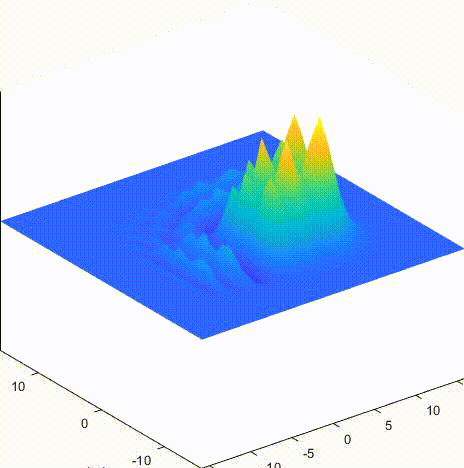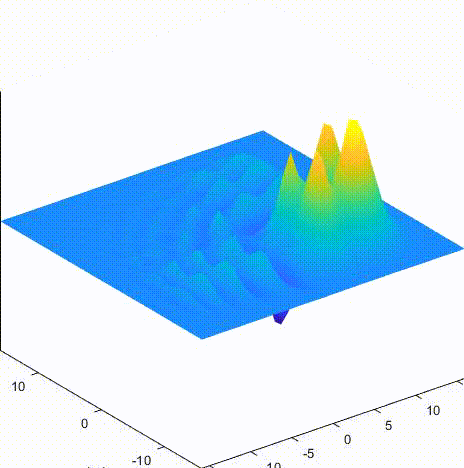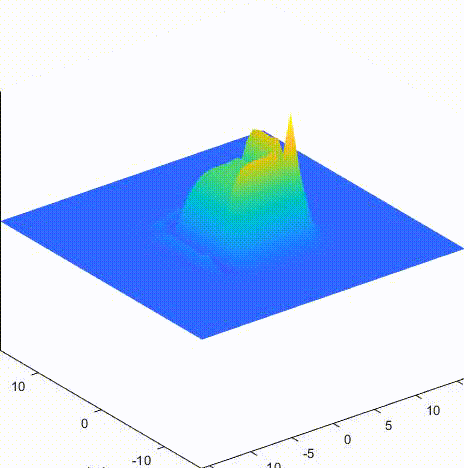
A 格式 dtdx = 0.5

B 格式 dtdx = 0.5
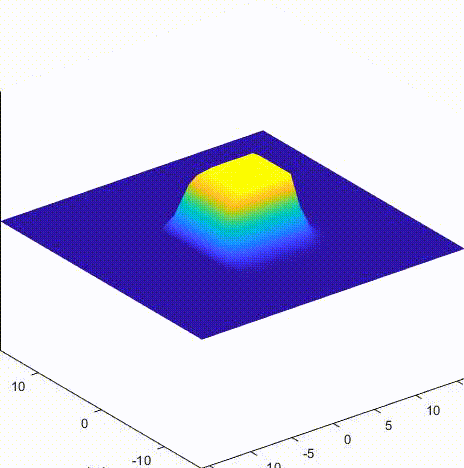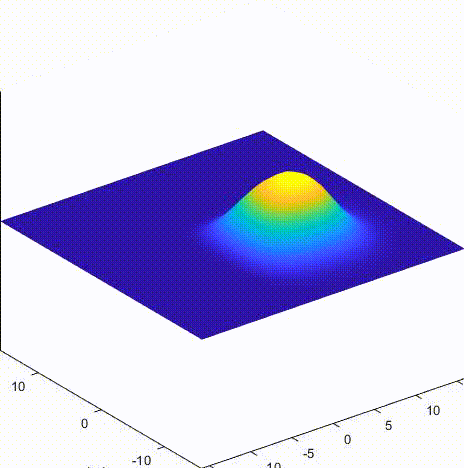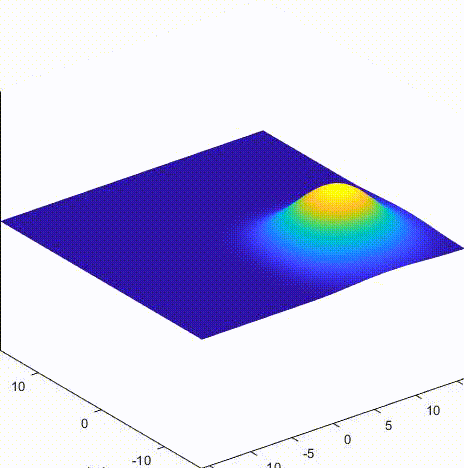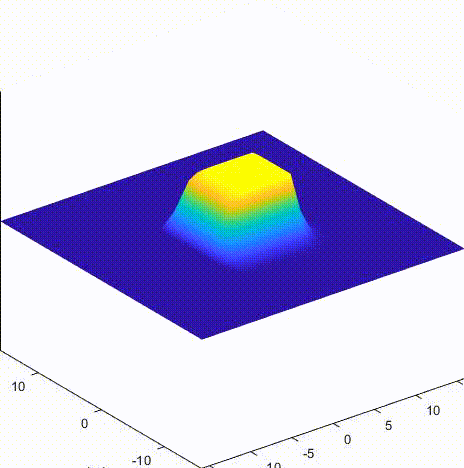
C 格式 dtdx = 0.5

LeapFrog 格式 dtdx = 0.5
5. 代码
% 中山大学 2019级 廉
clear;
clc;
clf;
% alpha X 对流项的系数
% beta Y 对流项的系数
% differenceBorder 差分边界
% 包含六个元素,从头到尾分别为 X 的下界,X 的上界,Y 的下界,Y 的上界,T 的下界,T 的上界
alpha = 1;
beta = 1;
differenceBorder = [-16 16 -16 16 0 20]';
% InitializationFun 初始化函数
% initializationBorder 初始化函数的边界
% 包含四个元素,从头到尾分别为 X 的下界,X 的上界,Y 的下界,Y 的上界
initializationBorder = [-4 4 -4 4]';
InitializationFun = @(X,Y) InRange(X,initializationBorder(1),initializationBorder(2)).*InRange(Y,initializationBorder(3),initializationBorder(4));
% dt 时间步长
% dtdx 时间步长比 X 步长
% dtdy 时间步长比 Y 步长
dx = 1;
dy = 1;
dtdx = [0.1 1 2]';
dtdy = [0.1 1 2]';
% 使用给定的差分格式,在给定的边界条件和初始条件下求解一维对流方程
% 并显示结果分析
% 由于误差累积,时间步越后的物理量误差越大。
% 为了清晰显示流场的解的趋势,这里使用 log 函数缩放整个流场,获得整个流场的解的数量级的分布。
% 由于流场的初始扰动的数量级很小,所以 log 缩放图上的点的可辨高度代表着误差大小,本质上该图只能显示误差的传播规律
% 为了显示初始扰动的传播规律,还需要从流场中取出包含初始扰动的一部分,放大来看。
for i = 1:1:max(size(dtdx))
[F,M] = ConvectionEqDifferenceMethod_2D(@DifferenceFormat_A_2D,'A', ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dx*dtdx(i),dx,dy);
videoName = sprintf("A_%d",i);
v = VideoWriter(videoName);
open(v);
writeVideo(v,M);
close(v);
end
for i = 1:1:max(size(dtdx))
[F,M] = ConvectionEqDifferenceMethod_2D(@DifferenceFormat_B_2D,'B', ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dx*dtdx(i),dx,dy);
videoName = sprintf("B_%d",i);
v = VideoWriter(videoName);
open(v);
writeVideo(v,M);
close(v);
end
for i = 1:1:max(size(dtdx))
[F,M] = ConvectionEqDifferenceMethod_2D(@DifferenceFormat_C_2D,'C', ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dx*dtdx(i),dx,dy);
videoName = sprintf("C_%d",i);
v = VideoWriter(videoName);
open(v);
writeVideo(v,M);
close(v);
end
for i = 1:1:max(size(dtdx))
[F,M] = ConvectionEqDifferenceMethod_2D(@DifferenceFormat_LeapFrog_2D,'LeapFrog', ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dx*dtdx(i),dx,dy);
videoName = sprintf("LeapFrog2_%d",i);
v = VideoWriter(videoName);
open(v);
writeVideo(v,M);
close(v);
end
function [F] = SignedLog10AbsClamp99(F)
% Lg 缩放
for i = 1:1:size(F,1)
for j = 1:1:size(F,2)
% 太小的取 0
if abs(F(i,j))<1
tmp = 1;
% 太大的取 99
elseif abs(F(i,j)) > 1e99
tmp = 1e99;
else
tmp = abs(F(i,j));
end
F(i,j) = log10(tmp)*sign(F(i,j));
end
end
end
function [X_Ans] = InRange(X,lower,upper)
% 在范围内返回 1
% 不在范围内返回 0
% 坐标系平移,使得区间原点为坐标系原点
mid = lower + (upper - lower)/2;
X_Ans = X - mid;
% 取每一个点到原点的长度
halfLength = upper - mid;
X_Ans = abs(X_Ans);
% 取每一个点到原点的长度与区间半长之间的关系
% 点在区间内,则值为 -1
% 点在边界,则值为 0
% 点在区间外,则值为 1
X_Ans = sign(X_Ans - halfLength);
% 每一个点减 1,使得点在区间内和点在边界这两种情况 -2 -1 都为负数,和点在区间外的情况 0 分离开
X_Ans = X_Ans - 1;
% 取每一个点在区间内外的关系
% 点在区间内或者在区间边界,则值为 -1
% 点在区间外,则值为 0
X_Ans = sign(X_Ans);
% 取每一个点在区间内外的关系
% 点在区间内或者在区间边界,则值为 1
% 点在区间外,则值为 0
X_Ans = abs(X_Ans);
end
function [Zeta_New] = MatrixTranslation(Zeta,xstep,ystep)
% 将矩阵在 x 方向上平移 xstep 个单位,在 y 方向上平移 ystep 个单位
% 这个平移不是仿射变换,只是元素相对位置的平移
% 空余的位置用 0 补充
% 移动距离超出矩阵长度的会得到全零
if abs(xstep) >= size(Zeta,1) || abs(ystep) >= size(Zeta,2)
Zeta_New = zeros(size(Zeta));
return;
end
Zeta_New = Zeta;
if xstep > 0
Zeta_New = Zeta_New(:,1:size(Zeta,2)-xstep);
Zeta_New = [zeros(size(Zeta,1),xstep) Zeta_New];
end
if xstep < 0
Zeta_New = Zeta_New(:,1-xstep:size(Zeta,2));
Zeta_New = [Zeta_New zeros(size(Zeta,1),-xstep)];
end
if ystep > 0
Zeta_New = Zeta_New(1+ystep:size(Zeta,1),:);
Zeta_New = [Zeta_New;zeros(ystep,size(Zeta,2))];
end
if ystep < 0
Zeta_New = Zeta_New(1:size(Zeta,1)+ystep,:);
Zeta_New = [zeros(-ystep,size(Zeta,2));Zeta_New];
end
end
function [Zeta_New] = DifferenceFormat_A_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 A 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
right = MatrixTranslation(Zeta,-1,0);
left = MatrixTranslation(Zeta,1,0);
up = MatrixTranslation(Zeta,0,-1);
down = MatrixTranslation(Zeta,0,1);
Zeta_New = Zeta - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
function [Zeta_New] = DifferenceFormat_B_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 B 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi,n))
right = MatrixTranslation(Zeta,-1,0);
up = MatrixTranslation(Zeta,0,-1);
Zeta_New = Zeta - alpha/2*dtdx*(right-Zeta) - beta/2*dtdy*(up-Zeta);
end
function [Zeta_New] = DifferenceFormat_C_2D(Zeta,alpha,beta,dtdx,dtdy)
% 二维对流方程 C 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n))/dt + alpha*(Zeta(xi,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n) - alpha/2*dt/dx*(Zeta(xi,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi,n)-Zeta(xi,yi-1,n))
left = MatrixTranslation(Zeta,1,0);
down = MatrixTranslation(Zeta,0,1);
Zeta_New = Zeta - alpha/2*dtdx*(Zeta-left) - beta/2*dtdy*(Zeta-down);
end
function [Zeta_New] = DifferenceFormat_LeapFrog_2D(Zeta,Zeta_Old,alpha,beta,dtdx,dtdy)
% 二维对流方程 蛙跳 格式
% (Zeta(xi,yi,n+1)-Zeta(xi,yi,n-1))/dt + alpha*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n))/(2*dx) + beta*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))/(2*dy) = 0
% => Zeta(xi,yi,n+1) =
% Zeta(xi,yi,n-1) - alpha/2*dt/dx*(Zeta(xi+1,yi,n)-Zeta(xi-1,yi,n)) - beta/2*dt/dy*(Zeta(xi,yi+1,n)-Zeta(xi,yi-1,n))
right = MatrixTranslation(Zeta,-1,0);
left = MatrixTranslation(Zeta,1,0);
up = MatrixTranslation(Zeta,0,-1);
down = MatrixTranslation(Zeta,0,1);
Zeta_New = Zeta_Old - alpha/2*dtdx*(right-left) - beta/2*dtdy*(up-down);
end
function [] = CEDM_2D_ParasValidater(DifferenceFormatFun,FormatName, ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dt,dx,dy)
% DifferenceFormatFun 差分函数
% alpha X 对流项的系数
% beta Y 对流项的系数
% differenceBorder 差分边界
% 包含六个元素,从头到尾分别为 X 的下界,X 的上界,Y 的下界,Y 的上界,T 的下界,T 的上界
% InitializationFun 初始化函数
% initializationBorder 初始化函数的边界
% 包含四个元素,从头到尾分别为 X 的下界,X 的上界,Y 的下界,Y 的上界
% dt 时间步长
% dtdx 时间步长比 X 步长
% dtdy 时间步长比 Y 步长
% 验证 alpha, beta 是否合法
if alpha == 0
error("alpha 需为非零!");
end
if beta == 0
error("beta 需为非零!");
end
% 验证 differenceBorder 是否合法
if min(size(differenceBorder)) ~= 1 || length(size(differenceBorder)) ~= 2
error("differenceBorder 需为一维向量!");
end
if max(size(differenceBorder)) ~= 6
error("differenceBorder 需有六个元素!");
end
if differenceBorder(1) > differenceBorder(2)
error("differenceBorder 中 X 的下界需要小于 X 的上界!");
end
if differenceBorder(3) > differenceBorder(4)
error("differenceBorder 中 Y 的下界需要小于 Y 的上界!");
end
if differenceBorder(5) > differenceBorder(6)
error("differenceBorder 中 T 的下界需要小于 T 的上界!");
end
% 验证 initializationBorder 是否合法
if min(size(initializationBorder)) ~= 1 || length(size(initializationBorder)) ~= 2
error("initializationBorder 需为一维向量!");
end
if max(size(initializationBorder)) ~= 4
error("initializationBorder 需有四个元素!");
end
if initializationBorder(1) > initializationBorder(2)
error("initializationBorder 中 X 的下界需要小于 X 的上界!");
end
if initializationBorder(3) > initializationBorder(4)
error("initializationBorder 中 Y 的下界需要小于 Y 的上界!");
end
% 验证 differenceBorder 与 initializationBorder 的相对关系是否合法
if differenceBorder(1) > initializationBorder(1)
error("differenceBorder 中 X 的下界需要小于 initializationBorder 中 X 的下界!");
end
if differenceBorder(2) < initializationBorder(2)
error("differenceBorder 中 X 的上界需要大于 initializationBorder 中 X 的上界!");
end
if differenceBorder(3) > initializationBorder(3)
error("differenceBorder 中 Y 的下界需要小于 initializationBorder 中 Y 的下界!");
end
if differenceBorder(4) < initializationBorder(4)
error("differenceBorder 中 Y 的上界需要大于 initializationBorder 中 Y 的上界!");
end
% 验证 dt 是否合法
if dt <= 0
error("dt 需为正数!");
end
% 验证 dx 是否合法
if dx <= 0
error("dx 需为正数!");
end
% 验证 dy 是否合法
if dy <= 0
error("dy 需为正数!");
end
end
function [FigHandle,Moive] = ConvectionEqDifferenceMethod_2D(DifferenceFormatFun,FormatName, ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dt,dx,dy)
% 使用给定的差分格式,在给定的边界条件和初始条件下求解二维对流方程
% 并显示结果分析
% DifferenceFormatFun 差分函数
% alpha X 对流项的系数
% beta Y 对流项的系数
% differenceBorder 差分边界
% 包含六个元素,从头到尾分别为 X 的下界,X 的上界,Y 的下界,Y 的上界,T 的下界,T 的上界
% InitializationFun 初始化函数
% initializationBorder 初始化函数的边界
% 包含四个元素,从头到尾分别为 X 的下界,X 的上界,Y 的下界,Y 的上界
% dt 时间步长
% dx X 步长
% dy Y 步长
% 验证参数合法性
CEDM_2D_ParasValidater(DifferenceFormatFun,FormatName, ...
alpha,beta,differenceBorder, ...
InitializationFun,initializationBorder, ...
dt,dx,dy);
% ---初始化---
x = differenceBorder(1):dx:differenceBorder(2);
y = differenceBorder(3):dy:differenceBorder(4);
t = differenceBorder(5):dt:differenceBorder(6);
% 求 X 和 Y 矩阵
% X 矩阵每一行都是 X 向量
% Y 矩阵每一列都是 Y 向量
% 和 XOY 坐标系的直觉相配
[X,Y] = meshgrid(x,y);
% Zeta 为待求物理量
Zeta = zeros(size(X));
% 初始化物理量矩阵
Zeta = InitializationFun(X,Y);
% 预分配影片帧数组
loops = max(size(t));
Moive(loops) = struct('cdata',[],'colormap',[]);
% ---画图---
% 新开一个绘图窗口,获取窗口句柄,方便导出 png
FigHandle = figure('Position',[400 400 600 600]);
% 保存影片帧的时候先隐藏绘图窗口
FigHandle.Visible = 'off';
% 设置坐标轴
axis([differenceBorder(1) differenceBorder(2) differenceBorder(3) differenceBorder(4) -2 2]);
axis manual;
ax = gca;
ax.NextPlot = 'replaceChildren';
% 添加标题
titleName = sprintf("Two-Dimensional Convection Equation ∂Zeta/∂t+alpha*∂Zeta/∂x+beta*∂Zeta/∂y = 0nDifference Format %s",FormatName);
title(titleName);
subtitleName = sprintf("alpha = %.4f, beta = %.4f, dt = %.4f, Δx = %.4f, Δy = %.4f",alpha,beta,dt,dx,dy);
subtitle(subtitleName);
% 添加坐标名
xlabel("x(m)");
ylabel("y(m)");
zlabel("Zeta");
% ---计算---
% 迭代时间步
for i = 1:1:max(size(t))
% 迭代
% 如果是蛙跳模式,就需要处理多个时间步的物理量矩阵
if FormatName == "LeapFrog"
% 如果处在第 1 个时间步,也就是初始状态时
% 那么蛙跳格式中的 (Zeta(xi,yi,n+1)-Zeta(xi,yi,n-1))/dt 中的
% Zeta(xi,yi,n-1) 不能赋 0 这会和初值产生梯度很大的冲突导致强烈的震荡
% 也不能令 Zeta_Old = Zeta;
% 也就是不能令蛙跳格式在第 1 个时间步取到的第 0 个时间步的物理量矩阵就是第 1 个时间步的矩阵
% 这样的话蛙跳格式就会退化成 A 格式
% 因此蛙跳格式只适合在已知上一时间步的物理量矩阵时使用
% 也就是要在第 2 个时间步或者更后的时间上使用
if i == 1
Zeta_New = DifferenceFormat_A_2D(Zeta,alpha,beta,dt/dx,dt/dy);
else
Zeta_New = DifferenceFormatFun(Zeta,Zeta_Old,alpha,beta,dt/dx,dt/dy);
end
Zeta_Old = Zeta;
Zeta = Zeta_New;
% 否则只需要一个时间步的物理量矩阵
else
Zeta = DifferenceFormatFun(Zeta,alpha,beta,dt/dx,dt/dy);
end
% ---画图---
% 平面着色
mesh(X,Y,Zeta,'LineStyle','none','FaceColor','interp');
% 捕获影片帧
drawnow;
Moive(i) = getframe;
end
% 保存影片帧完毕
FigHandle.Visible = 'on';
movie(Moive,1,30);
end
最后
以上就是留胡子金鱼最近收集整理的关于[计算流体力学][Matlab] 使用 A,B,C 格式与蛙跳格式求解二维对流问题的全部内容,更多相关[计算流体力学][Matlab]内容请搜索靠谱客的其他文章。




![[计算流体力学][Matlab] 使用 A,B,C 格式与蛙跳格式求解二维对流问题](https://www.shuijiaxian.com/files_image/reation/bcimg10.png)



发表评论 取消回复