USING INDUCTION TO DESIGN 使用归纳法设计算法 [3/14]

接上文：http://blog.csdn.net/jj12345jj198999/article/details/6602500

改进：第一个改进之处在于我们注意到在求解过程中存在很多冗余计算：x的指数是从头开始计算的。当我们计算x^n时通过使用x^(n-1)的值能够帮我们节省很多乘法运算。这些都是在归纳法假设中通过对x^n计算的归纳得以实现的：

更强的归纳假设：我们已经知道了如何去计算多项式Pn-1(x)，同时我们也知道如何计算x^(n-1)的值。

这个归纳假设更强一些，因为它要求计算出x^(n-1)，但是它拓展起来更容易。我们在计算x^n时仅仅需要进行一步乘法操作，然后在进行一步乘法操作得到an*x^n，然后进行一步加法操作完成整个计算。（其实这个假设并不是太强，因为我们还是需要计算x^(n-1)的值）。总而言之，这里需要进行2n次乘法和n次加法。尽管这个归纳假设需要更多的计算，但总的说来它减少了工作量。我们在后面再来讨论这一点。在各种层面上看来这个算法很好，它高效，简单也容易实现。然而存在一个更好的算法，它是通过用一种不同的方式使用归纳法得以实现的。

我们通过移去最后一个系数an来简化问题。（这是一个很直截了当的做法）但是我们也可以移去第一个系数a0。这个规模更小的问题变成了计算由an,an-1...a1这些系数组成的多项式，如下所示：
P'n-1(x)=an*x^(n-1)+an-1*x^(n-2)...+a1
（注意到an现在是n-1次的系数，后面依次改变）

新的归纳假设（倒序）：我们知道如何去计算由系数an,an-1...a1构成的x多项式（即上面列出来的P'n-1(x)）

由于这个假设更容易拓展，故其更符合我们的目的。很明显Pn(x)=x*P'n-1(x)+a0。因此这里仅仅只要一次乘法和一次加法就可以通过P'n-1(x)计算得出Pn(x)。完整的算法可以通过下面这个表达式加以描述：
an*x^n+an-1*x^(n-1)+...+a1*x+a0=((...((an*x+an-1)x+an-2)...)x+a1)x+a0

这个算法被称为霍纳归纳以W.G.Horner命名。（这也是牛顿提出来的）。下面给出了计算多项式的算法。

计算表达式算法
(a0,a1,a2...an,x:real); //输入a0至an,x,全为实数
begin
  P:=an;
  for i:=1 to n do
    P:=x*P+an-i;
end;

复杂度分析：这个算法仅仅需要n次乘法,n次加法以及一个额外的内存空间。尽管原先的解决方法看上去简单并且高效，但追求一个更好的算法是值得的。这个算法不仅仅是速度更快，同时相应的程序也更简单。

结论：上面给出的简单例子阐明了归纳法使用过程中的灵活性。霍纳规则的技巧仅在于考虑到输入是从左向右的，而不是直观上看到的从右向左。

当然这里有使用归纳法的许多其他潜在性，我们将在更多的例子中看到这一点。

找到一一映射关系【Q2】

f是一个把有限集合A映射到其自身的函数。（例如A中的每一个元素都映射到A中的另一个元素）为了简化起见，我们把A中的元素表示为从1到n的数字。我们假定函数f以一个数组f[1..n]的形式出现，这样f[i]存放的是f(i)的值。（该值是一个位于1到n之间的整数）当A中的每一个元素都仅仅只有一个元素对应它时我们把函数f称为一一映射。函数f可以用图1中的图加以展示，在图中，两端数据都对应同一个集合，图中的边表示映射关系。（这种映射关系是从左至右的）

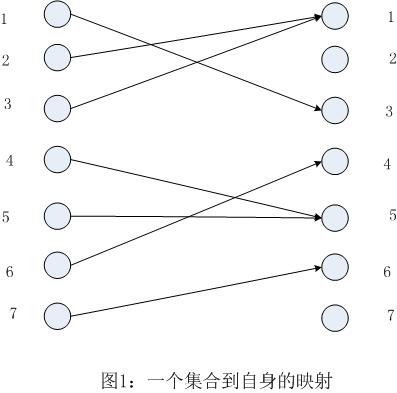
问题：找到一个包含最多元素的子集S(ScA)，使得函数f能够把S中的任何元素映射到S中的其他元素。(即f让S映射到自身)，同时S中的每一个元素仅仅只有唯一的一个S中的元素映射到自身。（即限制S让f成为一个一一映射）

如果f本来就是一个一一映射，那么全集A就满足了问题的条件，显然它也是最大的集合。在另一个方面来说，如果f(i)=f(j)存在且i≠j，那么集合S就不能同时包含i和j。例如在图1中S就不能同时包含2和3。不可能任意从两者中选择一个从集合中剔除出去。例如，假设我们决定删去3，由于1被映射到3，所以我们也必须删去1。（因为任意映射必须映射到S中而此时3已经不在S中了）。

最后

以上就是安静蚂蚁为你收集整理的USING INDUCTION TO DESIGN 使用归纳法设计算法 [3/14]的全部内容，希望文章能够帮你解决USING INDUCTION TO DESIGN 使用归纳法设计算法 [3/14]所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。