USING INDUCTION TO DESIGN 使用归纳法设计算法 [12/14]

接上文：http://blog.csdn.net/jj12345jj198999/article/details/6631122

稠密图中的最优匹配【Q9】【标题3】

在无向图G=(V,E)中一个匹配也就是一个没有公共顶点的边的集合。（一条边对应于两个点，一个点不可能对应于多余一个顶点）最大匹配是一个无法拓展的问题，意味着所有其他的边都至少与一个匹配的顶点相连。一个最大匹配也就是一个最大集。（一个最大匹配总是最大的，但是反过来说却未必正确）在图中一个拥有n条边和2n个点的匹配被称为最优匹配。（显然也是最大的）在这个例子中我们考虑一种很有限的情况。我们假设图中有2n个点，所有顶点的度都至少为n。可知在这些条件下总存在一个最优匹配。我们首先给出这个事实的证明，然后展示如何去修改这个证明从而得到一个查找最优匹配的算法。

证明采用的是最大的反例。考虑一个图G=(V,E)，其中|V|=2n每个顶点的度至少为n。如果n=1那么这个图仅仅有一条边连接两个顶点，这就是一个最优匹配。假设n>1时不存在这样一个最优匹配。考虑到最大匹配M属于E。由假设知|M|<n，同时由于任意一条边自己就是一个匹配显然有|M|≥1。既然M不是完全的（不包括所有的点），那么就存在至少两个不相邻点v1和v2不被包含在M中（即它们不对应M中的一条边）。这两个点至少有2n个不同的边从它们射出。所有这些边通向那些包含在M中的顶点，否则这样的边就不可能被加入到M中。由于M中边的数目小于n而且从v1到v2有2n条边与之相连，M中至少有一条边，假定为(u1,u2)，与从v1到v2的三条边相连。为了不失一般性，我们假设这三条边是(u1,v1),(u1,v2)和(u2,v1)（见图6）。很容易可以看到通过从M中移除(u1,u2)加上边(u1,v2)和(u2,v1)我们能够得到一个更大的匹配，这与之前最大的假设相矛盾。

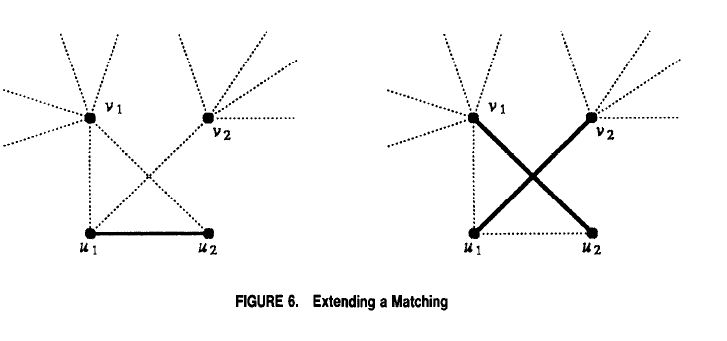
插入图6

第一眼看上去这个证明好像无法产生一个算法，因为证明是从一个最大匹配开始的。一旦我们知道如何去寻找这样一个匹配我们就能够解决这个问题。然而，使用反证法适用于任何最大化的匹配，这里展示的只是用于最大匹配而已。查找一个最大化的匹配要比查找一个最大匹配简单。我们只需要简单的添加不相连的边（即那些没有公共顶点的边）直到不存在这样的边的可能。然后我们使用上面描述的步骤把该匹配转换为一个更大的匹配。通过上面的证明我们可以不断反复执行直到找到一个最优匹配。

其他证明技巧【标题2】

在这篇论文中我们关注于基于归纳法的证明技巧。这里有很多其他的技巧和更多的类比，一些事很明显的，一些则不那么明显。许多数学定理的证明是使用一系列的前提得到的，这直接对应于在标准设计和结构化编程的思想。证明中使用反证法在算法设计中也有类似的地方。研究那些使用“类似的论据”证明的类比是很有趣的一件事。

我们这里简要列出四个证明技巧（其中的三个是基于归纳法的）以及它们的类比。更多的例子和类比可以在参考文献[12]中找到。

缩减法【标题3】

在证明定理和设计算法时，在问题之间使用缩减是一种很强大的技巧。如果问题A被指明是问题B的特例，那么解决B的算法可以被当成一个黑盒用来解决A。这个技巧对于解决下界和对问题进行分类也很有效（例如NP-完全问题）。如果已知问题A很难，那么问题B也至少一样难。

双倍归纳法【标题3】

这是一种使用归纳法针对一次多余一个变量的方法。它可用于在归纳法最佳序列不明确的情况，同时在针对几个变量依据一个特定的步骤在其中进行选择时，该方法也很容易使用到。例如，如果问题包含n个物品和一个k维空间时，我们可能想在算法执行时减少物品的数量或者物品尺寸的数量【见例4】。

最后

以上就是干净橘子为你收集整理的USING INDUCTION TO DESIGN 使用归纳法设计算法 [12/14]的全部内容，希望文章能够帮你解决USING INDUCTION TO DESIGN 使用归纳法设计算法 [12/14]所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。