USING INDUCTION TO DESIGN 使用归纳法设计算法 [9/14]

接上文：http://blog.csdn.net/jj12345jj198999/article/details/6619347

最近对【Q7】【标题3】

问题：给定平面上一个点的即可，找出最近两点之间的距离。

最直接使用归纳法的方法是移去一个点，解决n-1个点的问题，然后再考虑那个额外的点。然而，如果从对n-1个点的情况的求解中仅仅知道他们中间的最小距离，那么从额外点到其余n-1个点的距离都需要被计算出来。这样使得计算距离的总次数变成n-1+n-2+...+1=n(n-1)/2。（这其实是一个直接比较每两点的算法）我们想找到一个更快的解法。

一种分治算法

归纳假设如下所示：

归纳假设：我们已经知道在平面上如何去查找少于n个点中任意两点之间的最短距离。

既然我们假设我们能够解决少于n个点的子问题，我们可以把问题缩减为两个含有n/2个点的子问题。我们假设n是2的幂，这样我们总可以把一个集合分成数量两个相等的集合。（我们再后面再讨论这个假设）有很多方法可以把一个点集分成两个相等的部分。我们可以自由选择最好的方法。我们想要从规模较小问题的解法中获得尽可能多有用的信息，因此我们想要在考虑整个问题时尽可能多的保持有效。看起来这里把问题分解为两个不相关各含一半元素的部分是有道理的。当我们找到每个子集中最小的距离后，我们只需要关心那些靠近集合边界的点之间的距离。距离来说，对所有点进行排序最简单的方法是按照它们的x坐标进行排序，把平面用一条垂直线进行分割从而把集合一分为2（见图4）。（如果有一些点位于垂直线上我们任意把它们分配给两个集合中的一个，从而确保两个集合有相等的元素）我们选择这样划分的原因是使得合并解答时要做的工作尽可能少。如果这两个部分以某种方式交叉着，那样会使得对最近对点的检查变得更复杂。排序需要仅被执行一次。

给定一个集合P，我们按照上面的做法把它分解为P1和P2两个数量相等的子集。然后我们通过归纳法去查找每个子集中最近的两点距离。我们假设P1中最短的距离是d1，P2中是d2。不失一般性的，我们进一步假设d1≤d2。我们需要找到整个集合中最小的距离，也就是说我们需要去查找P1中的一个点到P2中的一个点是否有小于d1的距离。首先我们注意到只需要考虑以两部分中间的垂直线为中心宽度为2d1的带状范围内的点就足够了（见图4）。在该区域外的点中任意两点之间不可能拥有比d1更小的距离。通过上面的观察我们通常能够把很多点从考虑中排除，但是在最坏的情况下所有的点都可能仍位于这条带状区域中，对于它们我们无法使用直接的算法。

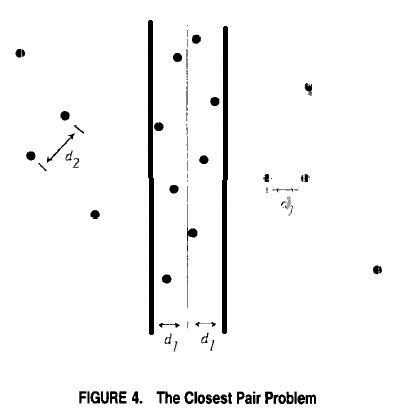
图4：最近对问题

另一个不是那么明显的观察点是对于在带中的任意点p，在另一边有很少的点到p点的距离要比d1小。原因在于在带中一边的所有点至少间隔为d1.假设p是带中的一个点，它的y坐标为yp，那么只需要考虑在另一边有坐标yq且满足|yp-yq|<d1的点即可。在带的每一边最多有六个这样的点（见图5中最坏的情况）。结果是如果我们以点的y坐标针对所有带中的点进行排序并且按顺序扫描这些点，我们只需要检查每一个点和按序排列中它的常数个邻居即可（而不是全部n-1个点）。我们在这里省略这个事实的证明（见例子[15]）。

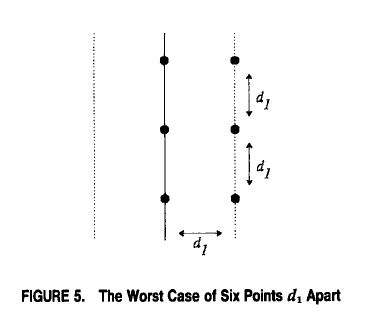
图5：最坏情况下六个相隔均为d1的点

最近对算法{首次尝试}
{p1,p2...pn:平面上的点}
begin
  按照点的x坐标对点进行排序{该排序只在开始时运行一次}
  把集合划分成两个相等的部分
  递归计算每个部分中最小的距离
  把d赋值为两个最小距离中的最小值
  排除出分割线d距离范围外的点
  按照y坐标对剩下的点进行排序
  按照y顺序扫描这些点并计算每个点和它的五个邻居之间的距离{事实上，4个就够了}
  if 这些距离中有小于d的 then
     更新d值
end;

复杂度：按照x坐标进行排序需要花费O(nlogn)时间，但是这仅仅需要执行一次。然后我们解决规模为n/2的两个子问题。排除出带状区域以外的点可以在O(n)的时间内完成。接下来在最坏的情况下按照y坐标对剩下的点进行排序需要O(nlogn)步。最终，扫描带中的点并在序列中把它与常数个邻居进行比较需要O(n)步。总的来说，为了在n个点中查找最近对，我们在含有n/2个点的子集中
找到两个最近对，然后花费O(nlogn)的时间去寻找两个子集之间的最近对(加上一次按照x坐标进行排序的时间O(nlogn))。带来的递推关系如下：

T(n)=2T(n/2)+O(nlogn), T(2)=1.

这个关系的解答是T(n)=O(n(logn)^2)。这比一个二次的算法要好，但是我们可以做的更好。现在我们来看看归纳法更巧妙的使用方法。【9/14】

最后

以上就是健壮龙猫为你收集整理的USING INDUCTION TO DESIGN 使用归纳法设计算法 [9/14]的全部内容，希望文章能够帮你解决USING INDUCTION TO DESIGN 使用归纳法设计算法 [9/14]所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。