USING INDUCTION TO DESIGN 使用归纳法设计算法 [8/14]

接上文：http://blog.csdn.net/jj12345jj198999/article/details/6616151

加强归纳假设【标题2】

在用归纳法证明数学定理时，加强归纳假设被当做一种很重要的技巧使用。当尝试使用一个归纳证明时常常会遇到下面的情况。定理用P(n)表示，归纳假设可以用P(n-1)表示，要证明结论P(n-1)推导出P(n)。很多情况下可以加上另一个假设，称为Q，在这个假设下证明会变得更简单。也就是说，证明P(n-1)和Q推导出P(n)要更加容易。这种结合的假设看上去是正确的但是还不清楚如何去证明。技巧在于在归纳假设中加上Q(如果可能的话)。现在需要证明[P和Q](n-1)推导出[P和Q](n)。结合的定理[P和Q]和仅有P相比是一个更强的定理，但是有时候更强的定理却更容易去证明（Polya称这个原理为“发明家的悖论”）。这个过程可以反复，加上正确补充的假设，定理的证明变得简单。我们在表达式计算和线段包含问题中已经初步看到了这个原理。

在这部分中我们给出两个例子来展现加强归纳假设的运用。第一个问题很简单，但它阐明了使用这种技巧时最常见的错误，也就是忽视了加入额外假设这个事实从而忘记更新证明过程。换句话说，证明P(n-1)和Q推导出P(n)时没有注意到Q是被假设的。我们可以把这种转换类比与解决更小的问题，不过该问题和原先的问题已经不是完全一样的了。第二个例子更复杂一些。

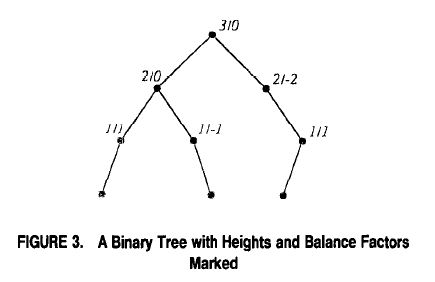
假设T是一个以r为根的二叉树。节点v的高度就是v和树中最底层的叶子之间的距离（应该是节点下方的树的最底层叶子）。节点v的平衡因子被定义为节点v的左孩子和它的右孩子（我们假设一个节点的孩子被标记为左和右）高度之差。图3给出了一棵树，在树中每个节点用h/b来标记，h是节点的高度，b是节点的平衡因子。

                        图3：一个由高度和平衡因子标记的二叉树

问题：给出一个拥有n个节点的树，计算它所有节点的平衡因子。

我们使用基本的归纳算法以及直截了当的归纳假设：

归纳假设：我们已经知道如何去计算小于n个节点的平衡因子。

最基本的n=1的例子很简单。给定一个拥有n>1节点的二叉树，我们移去根节点，然后用递归的方法解决剩下的子树。我们选择移去根节点因为一个节点的平衡因子仅仅依赖于节点下面的节点。我们现在已经知道出了根节点以外其他所有节点的平衡因子。但是根节点的平衡因子不是依赖于它的孩子的平衡因子而是依赖于它的孩子的高度。因此，一个简单的归纳法无法适用于这个例子。我们需要知道根节点孩子的高度。思想就在于在原先的问题中加上高度查询这个问题。

加强的归纳假设：我们已经知道如何计算小于n个节点的平衡因子以及它们的高度。

再一次的，基本问题很简单。现在考虑根节点时可以简单通过比较它的孩子的高度确定出它的平衡因子。此外，根节点的高度也能够被简单确定，也就是它两个孩子高度的最大值加上1。

这个算法的关键也就是解决一个简单拓展的问题。我们也计算高度而不只是计算平衡因子。拓展后的问题要更简单因为高度是很容易计算出来的。在很多情况下，解决一个更强的问题反而更简单。这对于归纳法说尤其正确。使用归纳法，我们仅需要把一个小问题拓展成一个更大的问题。如果解法更宽泛（因为问题被拓展了）那么归纳步骤可能要更简单因为我们有更多的东西可用。在该问题中常见的一个错误是忘记其中有两个不同的变量，而且这两个变量必须要单独计算。

最后

以上就是含糊项链为你收集整理的USING INDUCTION TO DESIGN 使用归纳法设计算法 [8/14]的全部内容，希望文章能够帮你解决USING INDUCTION TO DESIGN 使用归纳法设计算法 [8/14]所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。