S-LIME: Stabilized-LIME for Model Explanation
- 摘要
- 介绍
- 背景
- LIME
- 符号表
- 最优化
- LASSO和LARS
- LIME的不稳定性
- LASSO的不稳定性
- LARS决策的渐近性质
- S-LIME(稳定的LIME)
- 算法
- 变种
- 效率
- 实验证明
- 实验1 乳腺癌数据
- 不同模型的S-LIME也对稳定性有影响
- 样本数量
- MARS测试功能
- 基于EHR的败血症早期预测
- 讨论
摘要
黑盒的机器学习模型虽然效果较好,但缺乏解释性。基于扰动的事后解释(如LIME)被广泛用于在机器学习模型建立后对其进行解释。这类方法表现出很大的不稳定性,对方法本身的有效性提出了严重挑战,并损害了用户的信任。在本文中,我们提出了S-LIME,它利用基于中心极限定理的假设检验框架来确定保证结果解释稳定性所需的扰动点数量。在模拟数据集和真实数据集上的实验证明了该方法的有效性。
介绍
开发理解黑盒模型的方法,有助于增加用户信任、评估公平性和隐私、调试模型,甚至用于监管目的。
模型解释方法大致可分为两类:内在解释和事后解释。
具有内在可解释结构的模型包括线性模型、决策树,广义加性模型,等等。由于复杂性的限制,内在可解释模型通常不足以处理涉及异构特征和大量样本的现代任务。
事后解释可以在模型培训后提供见解。这些解释可以是特定于模型的,通常仅限于特定的模型类,例如基于树的方法的分割改进和卷积网络的显著性映射;或者模型不可知论者,不需要任何关于被检查模型内部结构的知识,分析通常通过评估一组扰动输入数据上的模型预测来进行。LIME和SHAP是两种最流行的模型不可知论解释方法。
事后解释模型也有一些缺陷。
- 广泛使用的排列重要性可以产生由于外推而具有高度误导性的诊断。
- 有研究可以产生对抗性干扰,这些干扰会产生感知上无法区分的输入,具有相同的预测标签,但却有非常不同的解释。
- 研究表明,解释算法可以被用来系统地合理化不公平黑盒模型的决策。
- 同时这些方法还有可能提供与原始模型计算结果不符的解释。
不稳定的解释无法让用户了解模型的实际工作原理,因此被认为是不可靠的。不幸的是,LIME并不总是稳定的。
我们提出了一个基于中心极限定理的假设检验框架,用于确定保证结果解释稳定性所需的扰动样本数。简单地说,LIME的工作原理是生成给定实例的扰动,并学习稀疏线性解释,其中稀疏性通常通过LASSO选择顶部特征来实现。LASSO早期会展示错误的发现+抽样过程中引入的随机性,导致实际显著的不稳定性。
我们仔细分析了生成LASSO路径的最小角度回归(LARS),并对选择下一个变量所涉及的统计数据进行了量化。基于假设检验过程,我们设计了一种新的算法S-LIME(Stabilized LIME),它可以自动自适应地确定保证稳定解释所需的扰动数量。
背景
LIME
符号表
| 名称 | 符号 |
|---|---|
| 黑盒模型 | f f f |
| 感兴趣的目标点 | x x x |
| x x x的扰动数据集 | D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) } w i t h y i = f ( x i ) D={(x_1, y_1), (x_2, y_2),…,(x_n,y_n)}quad with quad y_i=f(x_i) D={(x1,y1),(x2,y2),…,(xn,yn)}withyi=f(xi) |
| 扰动数量 | n n n |
| 可解释模型空间 | G G G |
| 可解释模型 | g ∈ G g in G g∈G |
最优化
a
r
g
m
i
n
g
∈
G
L
(
f
,
g
,
π
x
)
+
Ω
(
g
)
(
1
)
underset{g in G}{argmin}L(f,g,pi_x)+Omega(g) (1)
g∈GargminL(f,g,πx)+Ω(g)(1)
π
x
(
z
)
pi_x(z)
πx(z)是扰动实例z与x之间的接近度,通常被选为高斯核。
Ω
(
g
)
Omega(g)
Ω(g)是可解释模型的复杂度。例如决策树的深度,线性模型的非零权重个数。
L
(
f
,
g
,
π
x
)
L(f,g,pi_x)
L(f,g,πx)是在
π
x
pi_x
πx处,
f
f
f与
g
g
g之间不准确性的度量。
一项研究提出一种称为k-LASSO的程序,使用LASSO来选择顶部 k 个特征。 在这个案例中,
G
G
G是线性模型
g
=
ω
g
⋅
x
g=omega_gcdot x
g=ωg⋅x
L
(
f
,
g
,
π
x
)
=
∑
i
=
1
n
π
x
(
x
i
)
(
y
i
−
g
(
x
i
)
)
2
L(f,g,pi_x)=sum_{i=1}^npi_x(x_i)(y_i-g(x_i))^2
L(f,g,πx)=i=1∑nπx(xi)(yi−g(xi))2
Ω
=
∞
1
[
∣
∣
ω
g
∣
∣
0
>
k
]
Omega = infty mathbb{1}[||omega_g||_0 > k]
Ω=∞1[∣∣ωg∣∣0>k]
在这种情况下,(1)可以通过首先使用LASSO选择K个特征(使用正则化路径),然后通过最小二乘法学习权重来近似求解。
LASSO和LARS
β
^
L
A
S
S
O
=
arg
min
β
{
∑
i
=
1
n
(
y
i
−
β
0
−
∑
j
=
1
p
x
i
j
β
j
)
2
+
λ
∑
j
=
1
p
∣
β
j
∣
}
(
2
)
hat{beta}^{L A S S O}=underset{beta}{arg min }left{sum_{i=1}^{n}left(y_{i}-beta_{0}-sum_{j=1}^{p} x_{i j} beta_{j}right)^{2}+lambda sum_{j=1}^{p}left|beta_{j}right|right} (2)
β^LASSO=βargmin⎩⎨⎧i=1∑n(yi−β0−j=1∑pxijβj)2+λj=1∑p∣βj∣⎭⎬⎫(2)


算法1和算法2都可以容易地在数据集
D
D
D中加入权重向量
ω
=
(
ω
1
,
ω
2
,
…
,
ω
n
)
omega=left(omega_{1}, omega_{2}, ldots, omega_{n}right)
ω=(ω1,ω2,…,ωn),通过
D
=
{
(
ω
1
x
1
,
ω
1
y
1
)
,
(
ω
2
x
2
,
ω
2
y
2
)
,
…
,
(
ω
n
x
n
,
ω
n
y
n
)
}
mathcal{D}=left{left(sqrt{omega_{1}} x_{1}, sqrt{omega_{1}} y_{1}right),left(sqrt{omega_{2}} x_{2}, sqrt{omega_{2}} y_{2}right), ldots,left(sqrt{omega_{n}} x_{n}, sqrt{omega_{n}} y_{n}right)right}
D={(ω1x1,ω1y1),(ω2x2,ω2y2),…,(ωnxn,ωnyn)}
LIME的不稳定性
随机产生的扰动会导致产生的解释不稳定。我们将LIME应用于乳腺癌数据以说明这种现象。建立了一个包含500棵树的随机森林作为黑盒模型,我们使用LIME多次解释随机选择的测试点的预测。每次围绕测试点生成1000个合成数据,并通过LASSO选择前5个特征。我们重复实验100次,并计算特征的经验选择概率。结果如下图所示。
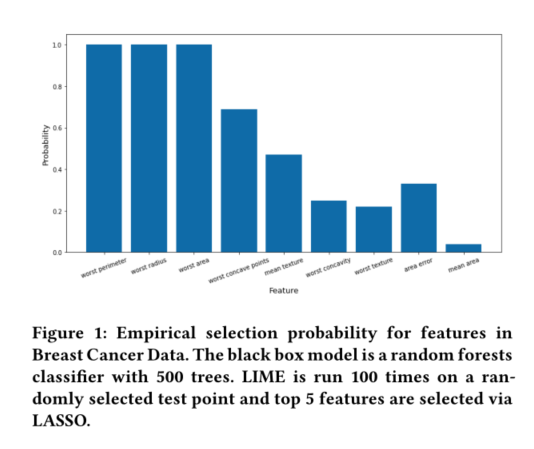
100次重复中,只有三个特征是由LIME一致选择的,而其余特征则有相当大的可变性。注意,这并不考虑所输入的特征的顺序:即使前三个特征在选择过程中表现出不同的排序。这个实验说明了LIME的一个重要缺点:不稳定或不可再生。这种不稳定性来自在围绕输入生成合成样本时引入的随机性,以及LASSO中使用的L1惩罚进一步增加了选择虚假特征的机会。
稳定LIME模型的一种方法是使用更大的合成数据集,但如果不进行重复实验,很难确定先验数据的大小。在下一节中,我们将研究特征选择在LASSO和LARS中是如何工作的,然后设计一种统计上合理的方法来自动自适应地确定保证稳定性所需的扰动数量。
LASSO的不稳定性
我们用一个简单的线性例子来说明这种现象。认为
t
=
ρ
1
x
1
+
ρ
2
x
2
+
ρ
3
x
3
t=rho_{1} x_{1}+rho_{2} x_{2}+rho_{3} x_{3}
t=ρ1x1+ρ2x2+ρ3x3。其中
x
1
,
x
2
,
x
3
x_1, x_2, x_3
x1,x2,x3.是独立的,由标准正态分布N(0,1)生成。请注意,我们在生成
y
y
y时不会施加任何额外的噪声. 我们选择
ρ
1
rho_{1}
ρ1 = 1,
ρ
2
rho_{2}
ρ2=0.75和
ρ
3
rho_{3}
ρ3=0.7,这样当一个人用LARS解LASSO时,
ρ
1
rho_{1}
ρ1始终先输入模型
ρ
2
rho_{2}
ρ2和
ρ
3
rho_{3}
ρ3系数更接近,更难区分。
进入模型的三个协变量的“正确”顺序应该是
(
x
1
,
x
2
,
x
3
)
(x_1,x_2,x_3)
(x1,x2,x3)。多次使用
n
=
1000
n=1000
n=1000的LASSO,观察到有20%的结果被
(
x
1
,
x
3
,
x
2
)
(x_1,x_3,x_2)
(x1,x3,x2)代替。如下图所示。
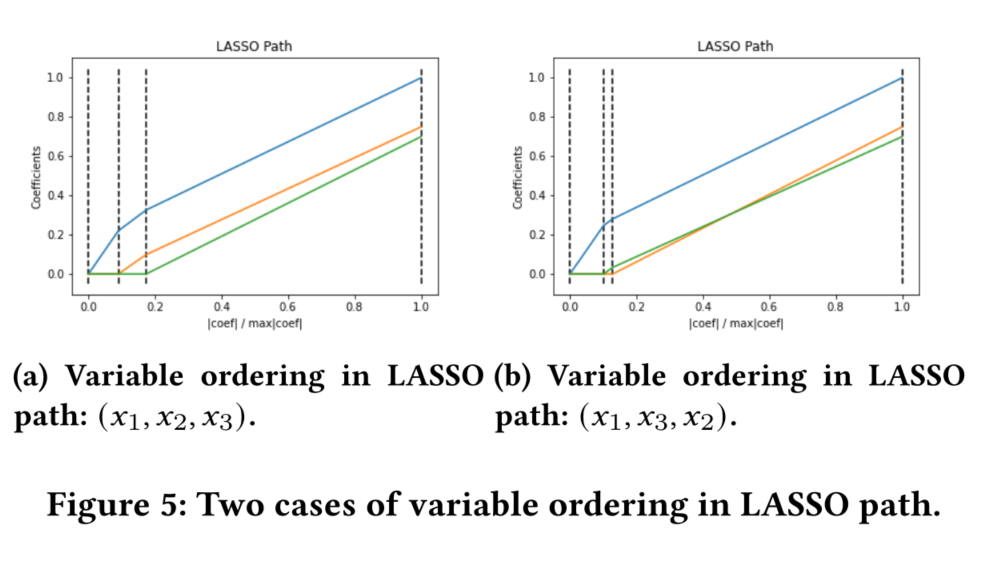
这个实验证明了LASSO本身的不稳定性。即使在这个理想的无噪声环境中,我们对变量采用高斯分布的独立设计,由于随机采样,20%的次数中,LASSO显示出不同的路径。直观地说,LASSO路径开始处的解是绝对有偏的,剩余向量包含许多真实效果。因此,一些不太相关或不相关的变量可能与残差表现出高度相关性,并且很早就被选中。
n
=
1000
n=1000
n=1000似乎是获得合理大量的一致性结果样本,但当应用S-LIME的概念,假设检验在第二步对
x
2
,
x
3
x_2,x_3
x2,x3进行选择时总是不确定的。在这种情况下,增加n确实可以产生显著的测试结果并稳定LASSO路径。
LARS决策的渐近性质
样本均值:我们有n个样本,每个样本的观测值为Xi,那么样本均值指的是
1
n
∗
∑
x
(
i
)
frac1n * sum x(i)
n1∗∑x(i),求n个观测值的平均值。
数学期望:就是样本均值,是随机变量,即样本数其实并不是确定的。
从概率论的角度而言:样本指的是我们现在有多少东西需要去观测,它是一种随机变量,即样本的多少是不确定的,我们得到的样本均值并不是真正意义上的期望。
| 名称 | 符号 |
|---|---|
| 残差 | r = ( r 1 , r 2 , … , r n ) boldsymbol{r}=left(r_{1}, r_{2}, ldots, r_{n}right) r=(r1,r2,…,rn) |
| 两个候选变量样本(特征) | x ⋅ i = ( x 1 i , x 2 i , … , x n i ) , x ⋅ j = ( x 1 j , x 2 j , … , x n j ) x_{cdot i}=left(x_{1 i}, x_{2 i}, ldots, x_{n i}right), x_{cdot j}=left(x_{1 j}, x_{2 j}, ldots, x_{n j}right) x⋅i=(x1i,x2i,…,xni),x⋅j=(x1j,x2j,…,xnj) |
| 两个有限样本估计(样本均值) | c ^ 1 = 1 n ∑ t = 1 n r t x t i , c ^ 2 = 1 n ∑ t = 1 n r t x t j hat{c}_{1}=frac{1}{n} sum_{t=1}^{n} r_{t} x_{t i},hat{c}_{2}=frac{1}{n} sum_{t=1}^{n} r_{t} x_{t j} c^1=n1∑t=1nrtxti,c^2=n1∑t=1nrtxtj |
| 对应随机变量 | R , X ⋅ i , X ⋅ j R, X_{cdot i}, X_{cdot j} R,X⋅i,X⋅j |
| 生成足够的数据以高概率返回与预期值相同的顺序的情况下的两个期望值 | c 1 = E ( R ⋅ X ⋅ i ) , c 2 = E ( R ⋅ X ⋅ j ) c_{1}=Eleft(R cdot X_{cdot i}right),c_{2}=Eleft(R cdot X_{cdot j}right) c1=E(R⋅X⋅i),c2=E(R⋅X⋅j) |
| 公式 f ( a 1 , a 2 ) f(a_1, a_2) f(a1,a2) | f ( a 1 , a 2 ) = a 1 − a 2 f(a_1,a_2)=a_1-a_2 f(a1,a2)=a1−a2 |
通过多元中心极限定理,我们可以得出:
存在
n
(
[
c
^
1
c
^
2
]
−
[
c
1
c
2
]
)
⟶
N
(
0
,
Σ
)
sqrt{n}left(left[begin{array}{l} hat{c}_{1} \ hat{c}_{2} end{array}right]-left[begin{array}{l} c_{1} \ c_{2} end{array}right]right) longrightarrow N(0, Sigma)
n([c^1c^2]−[c1c2])⟶N(0,Σ)
其
中
Σ
=
cov
[
R
⋅
X
⋅
i
R
⋅
X
⋅
j
]
=
[
σ
11
2
σ
12
2
σ
21
2
σ
22
2
]
其中Sigma=operatorname{cov}left[begin{array}{l}R cdot X_{cdot i} \ R cdot X_{cdot j}end{array}right]=left[begin{array}{ll}sigma_{11}^{2} & sigma_{12}^{2} \ sigma_{21}^{2} & sigma_{22}^{2}end{array}right]
其中Σ=cov[R⋅X⋅iR⋅X⋅j]=[σ112σ212σ122σ222]
在不丧失普遍性的情况下,我们假设
c
^
1
>
c
^
2
>
0
hat{c}_{1}>hat{c}_{2}>0
c^1>c^2>0。通常,如果相关性为负,我们可以简单地对本节中涉及的所有计算的相应特征值求反。设
Δ
^
n
=
c
^
1
−
c
^
2
hat{Delta}_{n}=hat{c}_{1}-hat{c}_{2}
Δ^n=c^1−c^2,
Δ
n
=
c
1
−
c
2
{Delta}_{n}={c}_{1}-{c}_{2}
Δn=c1−c2,考虑 f 函数:
n
(
f
(
[
c
^
1
c
^
2
]
)
−
(
f
[
c
1
c
2
]
)
)
⟶
N
(
0
,
σ
11
2
+
σ
22
2
−
σ
12
2
−
σ
21
2
)
sqrt{n}left(fleft(left[begin{array}{l} hat{c}_{1} \ hat{c}_{2} end{array}right]right)-left(fleft[begin{array}{l} c_{1} \ c_{2} end{array}right]right)right) longrightarrow Nleft(0, sigma_{11}^{2}+sigma_{22}^{2}-sigma_{12}^{2}-sigma_{21}^{2}right)
n(f([c^1c^2])−(f[c1c2]))⟶N(0,σ112+σ222−σ122−σ212)
或者可以近似为
Δ
^
n
−
Δ
n
∼
N
(
0
,
σ
^
11
2
+
σ
^
22
2
−
σ
^
12
2
−
σ
^
21
2
n
)
(
3
)
hat{Delta}_{n}-Delta_{n} sim Nleft(0, frac{hat{sigma}_{11}^{2}+hat{sigma}_{22}^{2}-hat{sigma}_{12}^{2}-hat{sigma}_{21}^{2}}{n}right) (3)
Δ^n−Δn∼N(0,nσ^112+σ^222−σ^122−σ^212)(3)
这些方差估计是根据样本值
r
t
x
t
i
r_{t} x_{t i}
rtxti and
r
t
x
t
j
,
t
=
1
,
…
,
n
r_{t} x_{t j}, t=1, ldots, n
rtxtj,t=1,…,n的经验协方差估计的。
假设我们有另一个独立生成的数据集
{
r
t
∗
,
x
t
i
∗
,
x
t
j
∗
}
t
=
1
n
left{r_{t}^{*}, x_{t i}^{*}, x_{t j}^{*}right}_{t=1}^{n}
{rt∗,xti∗,xtj∗}t=1n,根据(3)可得
(
A
−
C
)
−
(
B
−
C
)
=
A
−
B
(A-C)-(B-C)=A-B
(A−C)−(B−C)=A−B
Δ
^
n
∗
−
Δ
^
n
∼
N
(
0
,
2
⋅
σ
^
11
2
+
σ
^
22
2
−
σ
^
12
2
−
σ
^
21
2
n
)
hat{Delta}_{n}^{*}-hat{Delta}_{n} sim Nleft(0,2 cdot frac{hat{sigma}_{11}^{2}+hat{sigma}_{22}^{2}-hat{sigma}_{12}^{2}-hat{sigma}_{21}^{2}}{n}right)
Δ^n∗−Δ^n∼N(0,2⋅nσ^112+σ^222−σ^122−σ^212)
得到近似值
Δ
^
n
∗
∣
(
Δ
^
n
=
c
^
1
−
c
^
2
)
∼
N
(
c
^
1
−
c
^
2
,
2
⋅
σ
^
11
2
+
σ
^
22
2
−
σ
^
12
2
−
σ
^
21
2
n
)
hat{Delta}_{n}^{*} midleft(hat{Delta}_{n}=hat{c}_{1}-hat{c}_{2}right) sim Nleft(hat{c}_{1}-hat{c}_{2}, 2 cdot frac{hat{sigma}_{11}^{2}+hat{sigma}_{22}^{2}-hat{sigma}_{12}^{2}-hat{sigma}_{21}^{2}}{n}right)
Δ^n∗∣(Δ^n=c^1−c^2)∼N(c^1−c^2,2⋅nσ^112+σ^222−σ^122−σ^212)
为了控制在置信水平
1
−
α
1-alpha
1−α下的
P
(
Δ
^
n
∗
>
0
)
Pleft(hat{Delta}_{n}^{*}>0right)
P(Δ^n∗>0),我们需要让
c
^
1
−
c
^
2
>
Z
α
2
σ
^
11
2
+
σ
^
22
2
−
σ
^
12
2
−
σ
^
21
2
n
(
4
)
hat{c}_{1}-hat{c}_{2}>Z_{alpha} sqrt{2 frac{hat{sigma}_{11}^{2}+hat{sigma}_{22}^{2}-hat{sigma}_{12}^{2}-hat{sigma}_{21}^{2}}{n}} (4)
c^1−c^2>Zα2nσ^112+σ^222−σ^122−σ^212(4)
其
中
Z
α
是
标
准
正
态
分
布
下
的
(
1
−
α
)
分
位
数
其中Z_alpha是标准正态分布下的(1-alpha)分位数
其中Zα是标准正态分布下的(1−α)分位数
已知一个固定的置信水平
α
alpha
α和样本数量n,我们可以通过(4)得到对应的
p
p
p值
p
n
>
α
p_n>alpha
pn>α。
可以推出,
n
c
^
1
−
c
^
2
2
(
σ
^
11
2
+
σ
^
22
2
−
σ
^
12
2
−
σ
^
21
2
)
=
Z
p
n
sqrt{n} frac{hat{c}_{1}-hat{c}_{2}}{sqrt{2left(hat{sigma}_{11}^{2}+hat{sigma}_{22}^{2}-hat{sigma}_{12}^{2}-hat{sigma}_{21}^{2}right)}}=Z_{p_{n}}
n2(σ^112+σ^222−σ^122−σ^212)c^1−c^2=Zpn
最终可以推出需要的样本数量
n
′
n'
n′
n
n
′
=
Z
p
n
Z
α
(
5
)
sqrt{frac{n}{n^{prime}}}=frac{Z_{p_{n}}}{Z_{alpha}} (5)
n′n=ZαZpn(5)
S-LIME(稳定的LIME)
算法

变种
根据上一节中的理论分析,当一个新变量进入时,我们可以在每一步进行假设检验。如果测试结果显著,我们将继续下一步;否则,这表明扰动的当前样本量不够大。因此,我们根据方程式(5)生成更多的合成数据,并重新开始整个过程。
在实践中,我们需要设置生成的合成样本数的上限(用
n
m
a
x
n_{max}
nmax), 这样每当新的
n
′
n′
n′ 大于
n
m
a
x
n_{max}
nmax , 我们只需设置
n
=
n
m
a
x
n =n_{max}
n=nmax 最后一次通过外部while循环,每一步都不进行测试。这可以防止算法在两个相互竞争的特征在局部邻域中同等重要的情况下运行太长时间和浪费计算资源;例如,如果黑箱模型确实是局部线性的,两个预测因子的系数相等。
文中只对最相关的两个特征进行了比较,我们还可以用最相关的特征对其余所有特征进行比较。数学公式使用Bonferroni 修正为:
假设检验 H i , 0 : c ^ 1 ≤ c ^ i , i = 2 , … , p − m + 1 H_{i, 0}: hat{c}_{1} leq hat{c}_{i}, i=2, ldots, p-m+1 Hi,0:c^1≤c^i,i=2,…,p−m+1,获得 p p p值 p 2 , … , p p − m + 1 p_{2}, ldots, p_{p-m+1} p2,…,pp−m+1。
如果 ∑ i = 2 p − m + 1 p i < α sum_{i=2}^{p-m+1} p_{i}<alpha ∑i=2p−m+1pi<α,就拒绝无效假设。
人话说就是,如果在同一数据集上同时检验n个独立的假设,那么用于每一假设的统计显著水平,应为仅检验一个假设时的显著水平的1/n。
举个例子,如以显著水平0.05检验同一数据集上两个独立的假设,此时用于检验该两个假设应使用更严格的0.025;对于10000个基因的检验,若将p设置为10-6,进行10000次比较之后犯错误的概率是10-6*10000=0.01,完美的控制了假阳性的出现。
虽然很简单,但这种类似邦费罗尼的修正忽略了这些统计数据之间的大部分相关性,并将导致保守估计。在实验中,我们只对前两个特性进行假设测试,而不采用多重测试,因为这更有效,而且从经验上看,我们没有观察到任何性能下降。
效率
可以在算法3的基础上有一定的修改以提高效率,
- 重复使用现有的合成样本,只生成额外的 n ′ − n n'-n n′−n个样本。
- 在重新运行时,如果顺序与之前进入LASSO的顺序一致,则不需要假设检验,直至比之前运行了更多的路径,或出现不一致的情况下,再调用假设检验。
实验证明
以几个具体案例为例来说明S-LIME在生成稳定模型解释方面的有效性。Scikit-learn被用于构建黑盒模型。实验代码在 https://github.com/ZhengzeZhou/slime.
实验1 乳腺癌数据
数据集使用广泛采用的威斯康星州乳腺癌(诊断)数据集,其中包含569个样本和30个特征。一个包含500棵树的随机森林在80%的数据上作为黑盒模型进行训练,以预测一个实例是良性还是恶性。在剩下的20%测试数据上,它达到了大约95%的准确率。
在下面的图2中,我们展示了一个随机选择的测试实例上的四个LIME重复的图形说明,其中每个子图的左栏显示了选定的特征以及学习到的线性参数,右栏是样本的相应特征值。在同一实例上重复使用LIME,前两个特征的顺序不同,第四个和第五个特征的顺序也不一致。

为了量化生成解释的稳定性,我们测量了Jaccard指数,这是一种用于衡量样本集相似性和多样性的统计数据。给我两个数据集
A
A
A和
B
B
B (在我们的例子中,集合是从LIME中选择的特征),Jaccard系数定义为交叉点的大小除以并集的大小:
J
(
A
,
B
)
=
∣
A
∩
B
∣
∣
A
∪
B
∣
J(A, B)=frac{|A cap B|}{|A cup B|}
J(A,B)=∣A∪B∣∣A∩B∣
Jaccard索引的一个缺点是它忽略了每个功能集中的顺序。例如,如果两次迭代后返回的前两个特征是
A
=
{
A={
A={ worst perimeter, worst area
}
}
},
B
=
{
B={
B={ worst area, worst perimeter
}
}
},我们得到
J
(
A
,
B
)
=
1
J(A, B)=1
J(A,B)=1。这并不意味着LIME的解释是稳定的。为了更好地量化稳定性,我们查看了前k个特征的Jaccard指数,
k
=
1
,
…
,
5
k=1, ldots, 5
k=1,…,5。
表1显示了在所选测试实例上重复20次LIME和S-LIME的所有对的平均值。我们对于S-LIME设置
n
m
a
x
=
10000
n_{max} = 10000
nmax=10000。
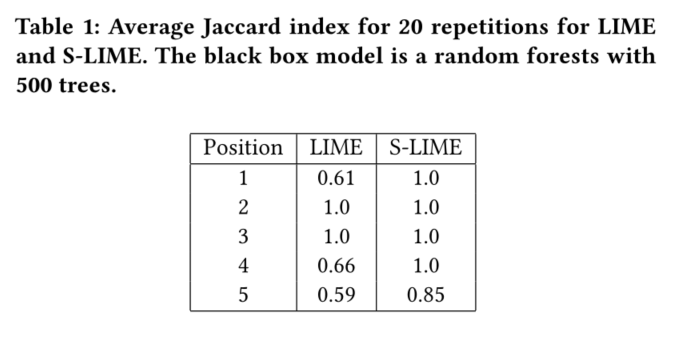
正如我们所见,对于前四个位置,S-LIME的平均Jaccard指数为1,这意味着该算法在不同的迭代中是稳定的。选择的第五个特征有一些变化,因为两个特征的平均半径和最差凹点在局部有非常接近的影响。进一步增加
n
m
a
x
n_{max}
nmax 将使第五个变量的选择更加一致。图3显示了我们在S-LIME模拟中观察到的仅有两种解释,其中差异在第五个变量。
作为对比,我们已经看到石灰的不稳定性,即使是第一个选择的变量。虽然LIME总是选择相同的前两个和第三个特征,但第四个和第五个特征的变化很大。本实验证明了S-LIME与LIME的稳定性。
不同模型的S-LIME也对稳定性有影响
除了在产生合成扰动时引入的随机性,模型解释算法的输出还取决于其他几个因素,包括黑箱模型本身。对一个给定实例的解释可能没有普遍的真理,因为它取决于基础模型如何捕捉协变量和响应之间的关系。不同的模型类型,甚至是通过随机初始化训练的相同模型结构,可以利用特征和响应之间的不同相关性,从而导致不同的模型解释。
在其他模型类型上应用S-LIME来说明两点:
- 与LIME相比,S-LIME可以产生稳定的解释,尽管对于某些模型类型,需要更多的合成扰动。
- 对于同一实例,不同的模型类型可以有不同的解释。这并不意味着S-LIME不稳定或不可再生,但从业者在应用任何模型解释方法时,需要意识到其对基础黑盒模型的依赖性。
我们使用支持向量机(SVM)和神经网络(NN)作为底层黑盒模型,并应用LIME和S-LIME。基本设置与第5.1节类似。对于SVM训练,我们使用默认参数2,其中应用了rbf核。NN由两个隐藏层构成,每个隐藏层分别有12个和8个隐藏单元。ReLU激活在隐藏层之间使用,而最后一层使用sigmoid函数输出概率。该网络在Keras中实现。这两种模型在测试集上都达到了90%以上的准确率。
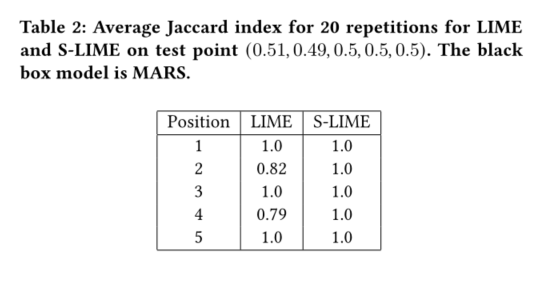
表4列出了随机选择的测试实例上每个设置20次重复的平均Jaccard索引。LIME由1000个合成样品生成,而S-LIME则由我们为SVM设定
n
m
a
x
=
100000
n_{max}=100000
nmax=100000和为NN设定n_{max} = 10000。与LIME相比,S-LIME在每个位置都具有更好的稳定性。
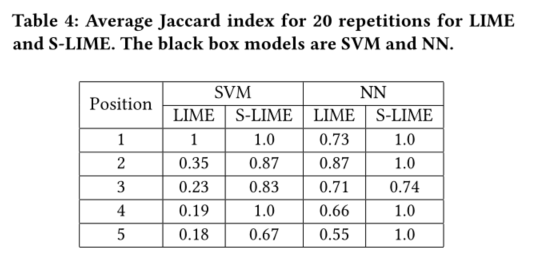
图6显示了S-LIME生成的SVM和NN黑箱模型解释的图形展示。我们可以看到,它们在选择的特征上有所不同。
因此可得出,潜在的黑盒模型也会影响局部解释的稳定性。
样本数量
对乳腺癌和败血症数据的大量测试样本进行了实验。
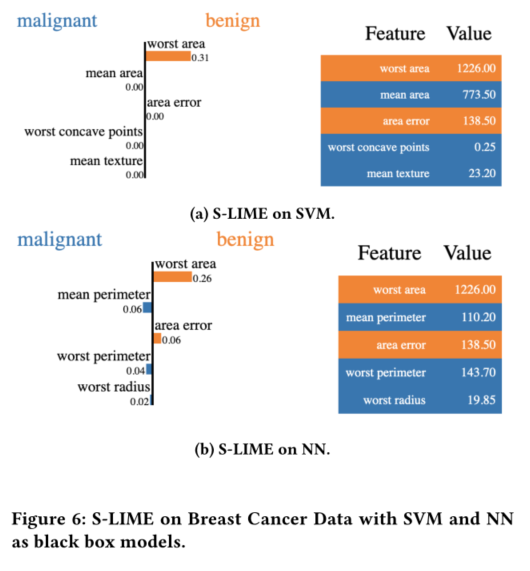
在每次应用中,随机选择50个测试样本。对于每个测试实例,LIME和S-LIME重复使用20次,像以前一样计算20对中所有对的平均Jaccard指数。最后,报告了50个测试样本的总体平均Jaccard指数。结果如表5所示。
使用1000个合成样本生成LIME解释。乳腺癌设置
n
m
a
x
=
10000
n_{max}=10000
nmax=10000,可以看到已经获得了很好的稳定性。败血症设置
n
m
a
x
=
100000
n_{max}=100000
nmax=100000,获得的稳定性仍然不是很好。因为有600个特征用于选择,如何使用LIME更有效地解释时间模型是未来的一个有趣方向。
MARS测试功能
设置
y
=
f
(
x
)
=
10
sin
(
π
x
1
x
2
)
+
20
(
x
3
−
0.05
)
2
+
5.2
x
4
+
5
x
5
y=f(x)=10 sin left(pi x_{1} x_{2}right)+20left(x_{3}-0.05right)^{2}+5.2 x_{4}+5 x_{5}
y=f(x)=10sin(πx1x2)+20(x3−0.05)2+5.2x4+5x5,其中
X
∼
U
(
[
0
,
1
]
5
X sim Uleft([0,1]^{5}right.
X∼U([0,1]5。测试点
x
x
x被选定为
(
0.51
,
0.49
,
0.5
,
0.5
,
0.5
)
(0.51,0.49,0.5,0.5,0.5)
(0.51,0.49,0.5,0.5,0.5)。我们可以很容易地计算周围五个变量的局部线性权重x预期的选择顺序是
(
x
3
,
x
1
,
x
2
,
x
4
,
x
5
)
left(x_{3}, x_{1}, x_{2}, x_{4}, x_{5}right)
(x3,x1,x2,x4,x5)。注意
x
1
x_1
x1和
x
2
x_2
x2,
x
3
x_3
x3和
x
4
x_4
x4的位置很难区分。
我们设置LIME为
n
=
1000
n=1000
n=1000,S-LIME为
n
0
=
1000
,
n
m
a
x
=
10000
n_0=1000, n_{max}=10000
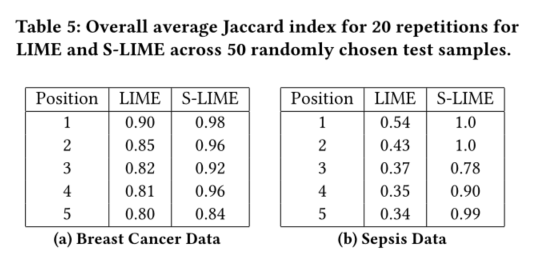
n0=1000,nmax=10000。可以看到Table2的结果。
基于EHR的败血症早期预测
从MIMIC-III收集数据,这是一个可自由访问的重症监护数据库。经过预处理后,队列中有15309名患者进行分析,其中1221名患者根据脓毒症-3临床标准发生脓毒症。对于每位患者,记录由每小时生命体征总结、实验室值和静态患者描述组成。ICULOS是一个时间戳,表示每个患者自ICU入院后的小时数,因此不直接用于训练模型。
变量列表如下图所示,
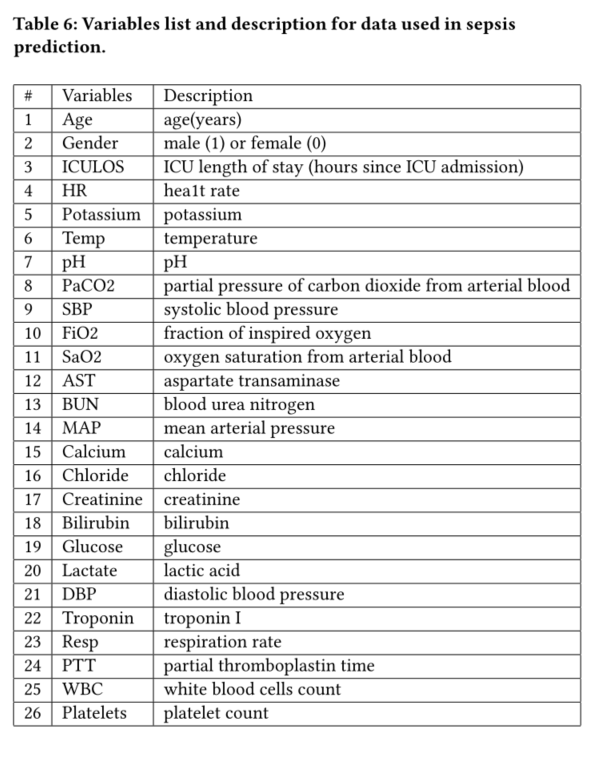
对于每个患者的记录,缺失的值将用最新值(如果可用)填充,否则为总体平均值。对阴性样本进行向下采样,以达到1:1的分类比率。我们随机选择90%的数据进行训练,剩下的10%用于测试。以Keras为例,建立了基于LSTM模块的简单递归神经网络。输入网络的每个样本有25个特征和24个时间戳,然后经过一个LSTM,其中32个内部单元的dropout为0.2,最后是一个密集层,通过softmax激活输出概率。Adam对网络进行了优化,初始学习率为0.0001,我们以50个批次的规模对其进行了500次训练。
时序数据的shape为
(
n
t
i
m
e
s
t
e
p
s
,
n
f
e
a
t
u
r
e
s
)
(n_{timesteps}, n_{features})
(ntimesteps,nfeatures),LIME将其reshape为
n
t
i
m
e
s
t
e
p
×
n
f
e
a
t
u
r
e
s
n_{_timestep } times n_{features}
ntimestep×nfeatures的长向量。其中设置LIME为
n
=
1000
n=1000
n=1000,S-LIME为
n
0
=
1000
,
n
m
a
x
=
10000
n_0=1000, n_{max}=10000
n0=1000,nmax=10000。表3显示了在两个随机选择的测试样本上,LIME和S-LIME选择的特征集的平均Jaccard指数。
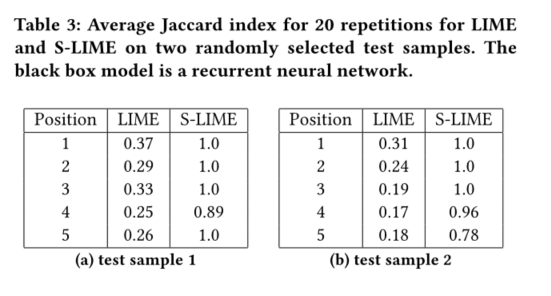
在本次实验中,LIME表现出不希望出现的不稳定性,这可能是由于应用了复杂的黑盒模型和大量特征(24×25=600)。与LIME相比,S-LIME获得了更好的稳定性,尽管仍然可以观察到在第二个测试样本中选择第五个特征时存在一些不确定性。
图4显示了两个不同测试样例上的S-LIME。我们可以看到,对于样例1,最新的温度以及最新的pH值和钾值起着重要作用。而对于样例2,最新的pH值是最重要的。

最终,本节中的实验证明了S-LIME在产生稳定解释方面的有效性。 同时提醒使用LIME时要格外小心,尤其是对于一些复杂的问题,局部线性模型具有一些特征,可能不适合近似建立在时间数据上的递归神经网络。如何将基于扰动的解释算法应用于时态数据仍然是一个开放的问题,将其留给未来的工作。
讨论
有一些相关工作:
- 例如确定LIME中的三个不确定性的来源是抽样方差、参数选择的敏感性和黑箱模型中的可变性。本文的目标是控制第一个可变性来源,因为其他两个取决于从业者的具体设计选择。
- 例如强调解释的稳定性和坚持性之间的权衡。他们的方法是为邻近性度量选择合适的内核宽度,但在给定任何内核宽度的情况下,这并不能提高稳定性。
- 例如设计了一个确定性版本的LIME,只通过分层聚类查看现有的训练数据,而不使用合成样本。然而,数据集中的样本数量会影响聚类的质量,缺少附近的点会带来额外的挑战;该策略还依赖于对训练数据的访问。
- 例如开发了一套工具,用于在贝叶斯框架中分析石灰的解释不确定性。
而本文的方法可以被视为一种频繁对应的方法,无需选择先验和评估后验分布。
还有一些工作采用生成对抗攻击帮助产生更真实的干扰样本,用于提高LIME的稳定性。
最后
以上就是繁荣身影最近收集整理的关于S-LIME阅读笔记(有实验代码)摘要介绍背景讨论的全部内容,更多相关S-LIME阅读笔记(有实验代码)摘要介绍背景讨论内容请搜索靠谱客的其他文章。
![bzoj 1022: [SHOI2008]小约翰的游戏John(反nim游戏)](https://www.shuijiaxian.com/files_image/reation/bcimg4.png)







发表评论 取消回复