【数学建模笔记】对策论

引言

对策论亦称竞赛论或博弈论。具有竞争或对抗性质的行为称为对策行为。在这类行为中。参加斗争或竞争的各方各自具有不同的目标和利益。为了达到各自的目标和利益，各方必须考虑对手的各种可能的行动方案，并力图选取对自己最为有利或最为合理的方案。对策论就是研究对策行为中斗争各方是否存在着最合理的行动方案，以及如何找到这个合理的行动方案的数学理论和方法。

对策问题

对策问题的特征是参与者为利益相互冲突的各方，其结局不取决于其中任意一方的努力而是各方所采取的策略的综合结果。
一个实际例子：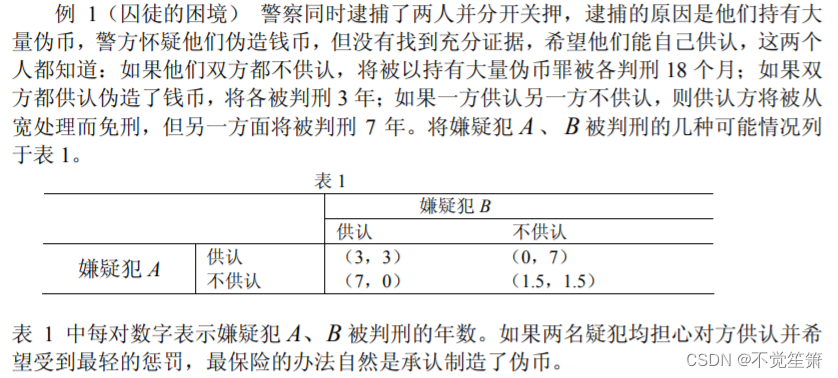

对策的基本要素

（1）局中人
在一个对策行为（或一局对策）中，有权决定自己行动方案的对策参加者，称为局中人。通常用 I 表示局中人的集合．如果有n 个局中人，则 I = {1,2,…,n}。一般要求一个对策中至少要有两个局中人。在例1中，局中人是 A、B 两名疑犯。
（2）策略集
一局对策中，可供局中人选择的一个实际可行的完整的行动方案称为一个策略。参加对策的每一局中人i ，i ∈ I ，都有自己的策略集$S_i$。一般，每一局中人的策略集中至少应包括两个策略。
（3）赢得函数(支付函数)
在一局对策中，各局中人所选定的策略形成的策略组称为一个局势，即若$s_i$ 是第i个局中人的一个策略，则n个局中人的策略组$s=(s_1,s_2,...,s_n)$就是一个局势。全体局势的集合S 可用各局中人策略集的笛卡尔积表示，即$S=S_1\ast S_2\ast ...\ast S_n$
当局势出现后，对策的结果也就确定了。也就是说，对任一局势， s∈S ，局中人i 可以得到一个赢得$H_i(s)$。显然，$H_i(s)$是局势 s 的函数，称之为第i 个局中人的赢得函数。这样，就得到一个向量赢得函数$H(s)=(H_i(s),...,H_n(s))$。

零和对策(矩阵对策)

零和对策是一类特殊的对策问题。在这类对策中，只有两名局中人，每个局中人都只有有限个策略可供选择。在任一纯局势下，两个局中人的赢得之和总是等于零，即双方的利益是激烈对抗的。

零和对策的混合策略

具有稳定解的零和问题是一类特别简单的对策问题，它所对应的赢得矩阵存在鞍点，任一局中人都不可能通过自己单方面的努力来改进结果。然而，在实际遇到的零和对策中更典型的是 μ + ν ≠ 0的情况。由于赢得矩阵中不存在鞍点，此时在只使用纯策略的范围内，对策问题无解。下面我们引进零和对策的混合策略。

零和对策的线性规划解法

当m > 2 且n > 2时，通常采用线性规划方法求解零和对策问题。
局中人Ⅰ选择混合策略 x 的目的是使得

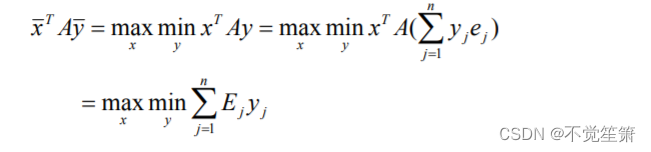
$\bar{x}$应为线性规划问题

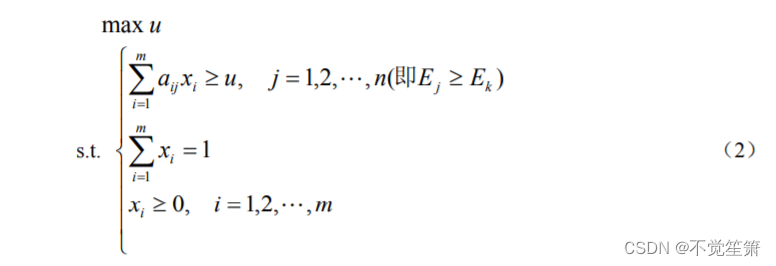
的解。同理，$\bar{y}$应为线性规划问题

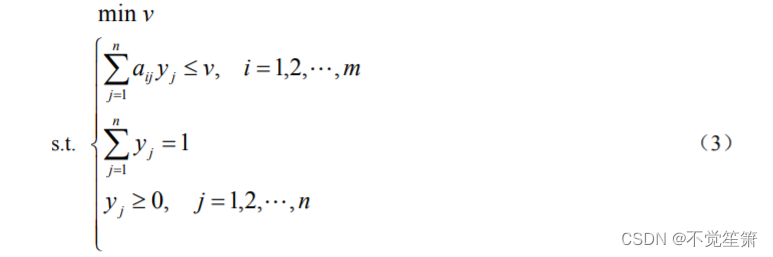
的解。

最后

以上就是着急含羞草为你收集整理的【数学建模笔记】对策论的全部内容，希望文章能够帮你解决【数学建模笔记】对策论所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。