基于地点相似度的POI推荐以及路径重组【matlab】

这里设计的POI推荐算法是参考于POI推荐算法，简单来说，就是利用用户访问POI的频次作为POI之间相似度的测度。

具体描述以及代码展示如下：

• 数据预处理

1. 随机抽取若干行数据

首先我们要进行数据清洗，我们将456967行数据，10000多名用户参与的Gowalla数据进行预处理

为避免数据的偶然性对实验产生的偏差影响，我们在获取数据的同时，随机抽取10000行数据进行实验，代码如下：

clear all
[data,txt]=xlsread('Gowalla.xlsx','Sheet1','A1:D456968');
[m,n]=size(data);
collect=10000;
Data=data(randperm(m, collect),:);%随机抽取10000行数据
[M,N]=size(Data);
count=0;
t=10;
xlswrite('Gowalla_1',Data,'A2:D10001');
%记住：生成文件后，要按照user_id序号升序或降序排列，然后再运行下一个代码文件

生成Excel文件后，按照用户编号升序或者降序排列，因为在下面过滤数据的操作中，需要利用这样的排列结构进行过滤操作

     2.数据过滤

过滤掉同一个user_id下，记录少于10行的数据，这样，保留下来的user_id，至少拥有10次访问Poi的签到数据

代码如下：

clear all
[Data,TxT]=xlsread('Gowalla_1','Sheet1','A1:D10001');
[M,N]=size(Data);
count=1;
t=10;
i=2;
while i<=M%过滤掉记录少于10的行数据
    if Data(i,1)==Data(i-1,1)%如果上下两行的用户ID数据一致
        count=count+1;%计数+1
    else   %如果出现上下两行不一致，则代表着上一个用户所有的数据记录读取完毕；
        if  count<t
            Data(i-count:i-1,:)=[];%删除
            i=i-count;%i回溯，因为删除数据后，原始矩阵维度已经发生变化
            count=1;
        else
            count=1;%这里是count>t的情况，重新计数
        end
    end
     i=i+1;
end
xlswrite('Gowalla_2',Data);
%记住：生成后的Gowalla_2文件要按照poi序号从小到大排列

• 算法设计

下面来逐行用代码解释算法每一步操作步骤

1）输入地点a, 用户集合X，地点集合Y、用户和地点关系集合
2）找到对a感兴趣的用户子集U；

clear all
clc
[Data,TxT]=xlsread('Gowalla_2','Sheet1');
[M,N]=size(Data);
u=zeros(M,1);
theta=2;
count=1;
for i=[1:1:M-1]
  if (Data(i,1)==Data(i+1,1))&& (Data(i,2)==15693) && (Data(i,2)==Data(i+1,2))
      if count < theta
          count=count+1;
      else
          u(i,1)=Data(i,1);
            count=1;
      end
  end
  if (Data(i,1)~=Data(i+1,1))&& (count >= theta)
      u(i,1)=Data(i,1);
      count=1;
  end
end
user=unique(u);
user(any(user,1),:)=[];%因为使用unique函数，使得函数值为0的只有一行
User=user';
[M_user,N_user]=size(User);

在我们的实践中，设地点a为poi_id是15693的节点，阈值设为theta=2,即同一个用户访问同一个Poi的次数超过theta，我们可以认为该用户对该poi感兴趣

3）分别找到U中用户感兴趣的地点，组成地点子集A

p=zeros(M,1);
Count=1;
for i=[1:1:M-1]
    if ismember(Data(i,1),User)&&(Data(i,2)==Data(i+1,2))
        if Count < theta
            Count=Count+1;
        else
            p(i,1)=Data(i,2);
            Count=1;
        end
    end
end
poi=unique(p);
poi(any(poi,1),:)=[];
Poi=poi';
[M_poi,N_poi]=size(Poi);

4）分别计算A中元素e和a的相似度
    sim = |U中去过e的人次| / sqrt(|X中去过a的人次| * |X中去过e的人次|)
    这里用了人次，而没有用人数
5）按sim对A中元素从大到小排序，取sim最大的n个地点作为a的相似地点子集S
6）输出S

count_1=0.1*ones(1,N_poi);%计算集合User中访问Poi集合当中元素的人次
count_2=0;%计算分母1
count_3=0;%计算分母2

for i=[1:1:N_user]
    for k=[1:1:N_poi]
        for j=[1:1:M]
            if ismember(Data(j,1),User) && ismember(Data(j,2),Poi) && (Data(j,2)==Poi(1,k))
                    count_1(1,k)=count_1(1,k)+1;
            end
        end
    end
end

count_1=round(count_1);

for i=[1:1:M]
  if Data(i,2)==15693
      count_2=count_2+1;
  end
end

for i=[1:1:M]
    if ismember(Data(i,2),Poi)
        count_3=count_3+1;
    end
end

sim=count_1;
for i=[1:1:N_poi]
    sim(1,i)=sim(1,i)/sqrt(count_2*count_3);
end
[S,Ind]=sort(sim);

在这里顺便值得一提的是，在初始化count_1向量时，之所以设置为0.1*ones()矩阵，是因为这巧妙的规避了poi或者是用户编号为0的误差，因为我们之前使用类似功能的any()函数保留了非零元，之后再“四舍五入”，round（）一下，这样原本为0.1的数据依然是0，我们就可以放心的将此零元“过滤掉”（unique函数过滤）

• 进行个性化选择

考虑到用户可能有几日游的习惯，我们设置Day变量，下面是假设，假设用户半日游，如下，则给我们推荐3个景点，分别是Sim值较高的前三个POI节点。如下所示：

Day=0.5;
if Day==0.5
    N=3;
    X=['为您推荐半日游，推荐',num2str(N),'个景点','它们分别是',num2str(Poi(1,Ind(1,N_poi:-1:N_poi-N+1)))];
    table=Poi(1,Ind(1,N_poi:-1:N_poi-N+1));
    Table=zeros(N,3);
    Table(:,1)=table';
    for i=[1:1:N]
        for j=[1:1:M]
            if Table(i,1)==Data(j,2)
                Table(i,2)=Data(j,3);
                Table(i,3)=Data(j,4);
            end
        end
    end
    disp(X);
     xlswrite('半日游推荐结果',Table);
end
if Day==1;
   N=5;
    X=['为您推荐一日游，推荐',num2str(N),'个景点','它们分别是',num2str(Poi(1,Ind(1,N_poi:-1:N_poi-N+1)))];
    table=Poi(1,Ind(1,N_poi:-1:N_poi-N+1));
    Table=zeros(N,3);
    Table(:,1)=table';
        for i=[1:1:N]
        for j=[1:1:M]
            if Table(i,1)==Data(j,2)
                Table(i,2)=Data(j,3);
                Table(i,3)=Data(j,4);
            end
        end
    end
    disp(X);
    xlswrite('一日游推荐结果',Table);
end
if Day==2
    N=7;
    X=['为您推荐两日游，推荐',num2str(N),'个景点','它们分别是',num2str(Poi(1,Ind(1,N_poi:-1:N_poi-N+1)))];
    table=Poi(1,Ind(1,N_poi:-1:N_poi-N+1));
    Table=zeros(N,3);
    Table(:,1)=table';
        for i=[1:1:N]
        for j=[1:1:M]
            if Table(i,1)==Data(j,2)
                Table(i,2)=Data(j,3);
                Table(i,3)=Data(j,4);
            end
        end
    end
    disp(X);
     xlswrite('两日游推荐结果',Table);
end

• 最后进行路径重组

我们使用Ant Colony算法进行路径重组，由于原始Gowalla数据格式不包含坐标信息，因此我们要将经纬度进行转化计算，这里可以参考我写的程序，启发函数为欧氏距离的倒数，其结果如下所示：

推荐POI节点

原始数据展示

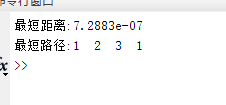
推荐的路径结果与距离

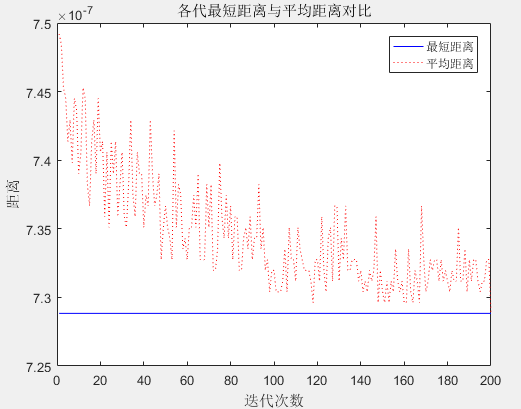
各代最短距离与平均距离的对比

最后

以上就是尊敬皮带为你收集整理的基于地点相似度的POI推荐以及路径重组【matlab】的全部内容，希望文章能够帮你解决基于地点相似度的POI推荐以及路径重组【matlab】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。