概述
马尔科夫不等式、霍夫丁不等式和詹森不等式，是机器学习中经常遇到的几个概率不等式。本文对它们进行简单介绍，并加以证明，然后对它们在机器学中的应用进行举例说明。
主要内容包括：
马尔科夫不等式（Markov’s Inequality）
定义
证明
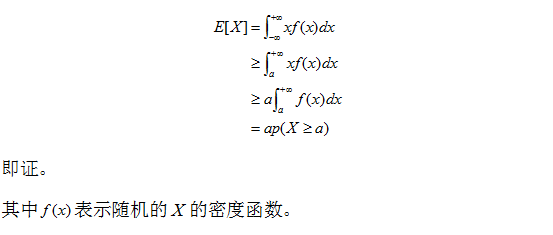
应用
a.用于估计一个概率的上界，比如假设你所在公司的人均工资是1万，那么随机选一个你司员工，其工资超过10万的概率，不会超过1/10。
b.用于其他概率不等式的证明，比如下面的霍夫丁不等式。
霍夫丁不等式（Hoeffding’s Inequality）
霍夫丁不等式的证明，除了要用到上面的马尔科夫不等式外，还要用到霍夫丁引理。因此，下面先介绍霍夫丁引理。
霍夫丁引理
定义
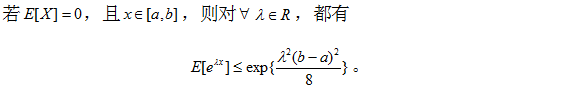
证明
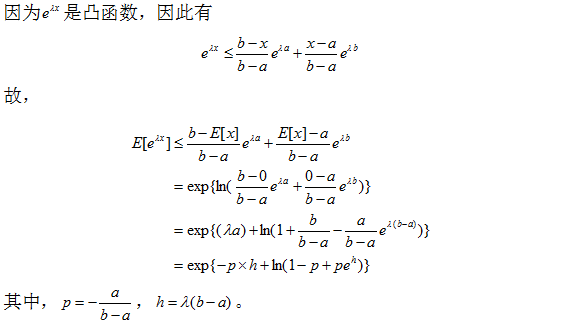
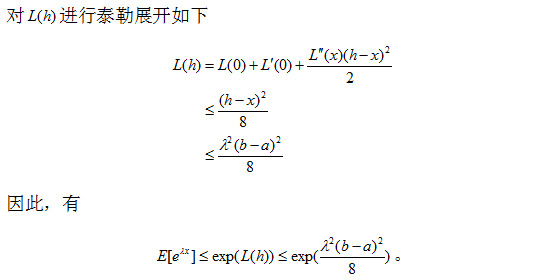
霍夫丁不等式
定义
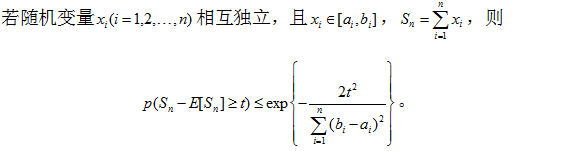
证明
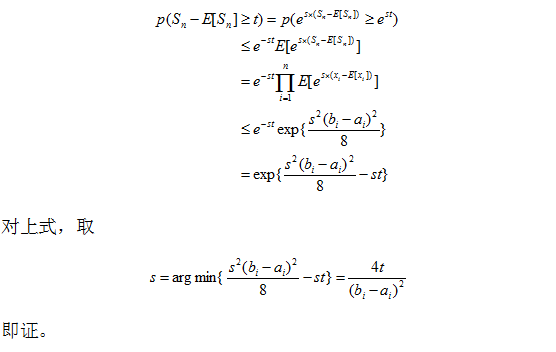
应用
用于给出二分类问题的泛化误差上界
詹森不等式（Jensen’s Inequality）
定义
证明
凸函数定义 + 归纳法
应用
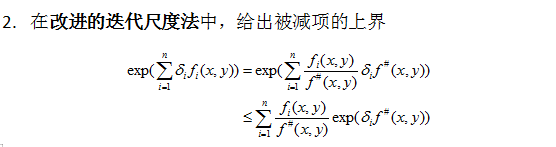
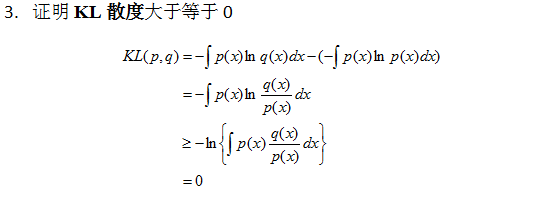
小结
1. 有些公式里很多变量没给出来具体意义啊？
如果你已学过相关内容，这里可以帮助你回顾一下；如果你还没学习相关内容，不必了解其中变量的具体含义，这里重在形式推导。
2. 咦，那么巧？概率统计中log和exp的函数形式如此常见（比如，对数似然函数、指数分布族），而-log(x)和exp(x)刚好都是凸函数，可以各种使用詹森不等式。
NO，是因为-log(x)是凸函数，我们才对似然函数求对数，因为exp(x)是凸函数，我们才更喜欢用指数分布族建模的。所以，那么多的偶遇其实都是注定，因为那个他（她）早在那里等你多时了！
参考文献：
李航 《统计学习方法》 第二版
最后
以上就是无情小刺猬为你收集整理的机器学习中常用的几个概率不等式及证明的全部内容，希望文章能够帮你解决机器学习中常用的几个概率不等式及证明所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复