作业题目

已知有20个样本，每个样本有2个特征，数据分布如下表所示，使用K均值法或K中心点法实现样本分离。要求：需要有结果展示，需要对方法和模型进行评价。
样本序号 1 2 3 4 5 6 7 8 9 10
特征1 0 1 0 1 2 1 2 3 6 7
特征2 0 0 1 1 1 2 2 2 6 6

样本序号 11 12 13 14 15 16 17 18 19 20
特征1 8 6 7 8 9 7 8 9 8 9
特征2 6 7 7 7 8 8 8 9 9 5

K均值原理

K-Means算法是一种无监督分类算法，假设有无标签数据集：
$$X=[x^{(1)},x^{(2)},x^{(3)}...x^{(m)}{]}^T$$
该算法的任务是将数据集聚类成k个簇，$c=c_1,c_2,c_3,\dots \dots ,c_k$.最小化损失函数为：
$$E=\sum _{i=1}^k\sum _{x\in C_i}||x-{\mu }_i|{|}^2$$
其中${\mu }_i$为簇$c_i$的中心点：
$${\mu }_i=\frac{1}{C_i}\sum _{x\in C_i}x$$
要找到以上问题的最优解需要遍历所有可能的簇划分，K-Means算法使用贪心策略求得一个近似解，具体步骤如下：
1）随机选取k个点作为各个簇的中心点；
2）计算所有样本点与各个簇中心之间的距离，然后把样本点划入最近的簇中；
3）根据簇中已有的样本点，重新计算簇中心；
4）重复2、3。
在python机器学习库中有kmeans算法的函数，我们可以利用该函数完成相关聚类分析操作。

python编程

聚类分析

首先，调用KMeans.fit函数，对feature进行K均值分类，n_clusters为分类类数。
clf = KMeans(n_clusters=4).fit(feature)
之后利用Kmeans.fit_predict函数对feature按之前的中心点进行分类。
label = KMeans(n_clusters=4).fit_predict(feature)

模型评价

1）轮廓系数
from sklearn.metrics import silhouette_score
从sklearn.metrics中调用silhouette_score函数，可以利用轮廓系数评价分类体系，可以将轮廓系数与分类个数化为曲线，曲线斜率变化最大的地方，分类效果越好。
2）Calinski-Harabasz指数评价
from sklearn.metrics import calinski_harabasz_score
从sklearn.metrics中调用calinski_harabasz_score函数，该函数可以直接对聚类模型进行打分。

分类结果

首先，运行分类模型评价程序，决定数据类别个数。在轮廓系数评价体系下，画出曲线为：

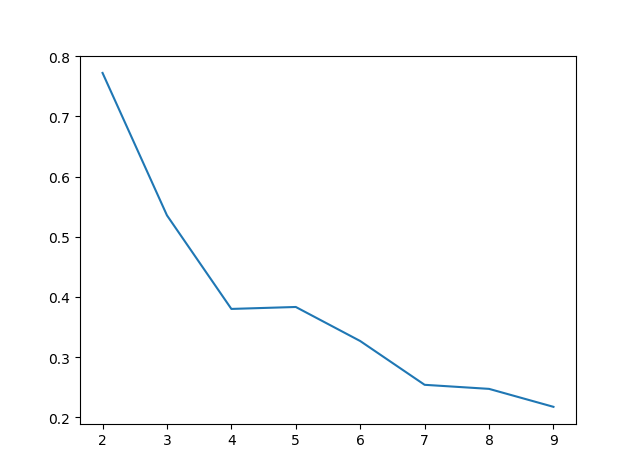
可以发现在类别数较少的情况下曲线斜率更大，分类效果更好。在Calinski-Harabasz指数评价下：

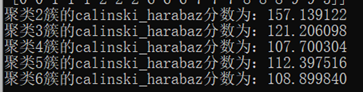
由此可知，将数据分为两类时分类效果最好。
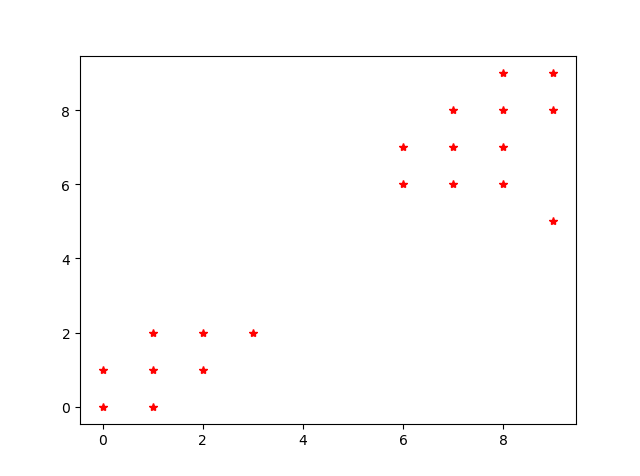
在未分类前，数据的散点示意图如图所示：

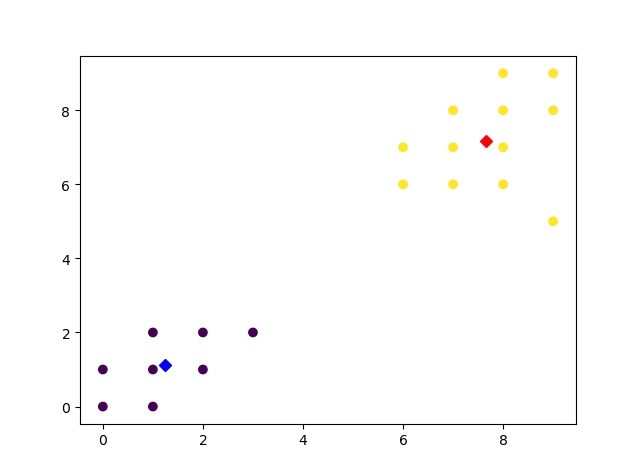
分为两类后，有：

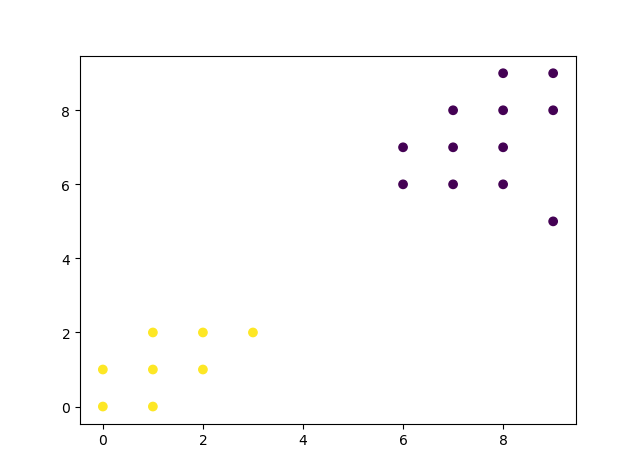
画出聚类中心点位置：

python代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.metrics import calinski_harabasz_score

feature_1 = [0,1,0,1,2,1,2,3,6,7,8,6,7,8,9,7,8,9,8,9]
feature_2 = [0,0,1,1,1,2,2,2,6,6,6,7,7,7,8,8,8,9,9,5]

#plt.plot(feature_1,feature_2,'r*')
#plt.show()

feature = np.vstack((feature_1,feature_2))

print(feature)
feature = np.transpose(feature)

clf = KMeans(n_clusters=2).fit(feature)

print (clf.cluster_centers_)
print (clf.labels_)
print (clf.inertia_)

df = clf.cluster_centers_
label = KMeans(n_clusters=2).fit_predict(feature)
plt.scatter(feature[:,0],feature[:,1],c=label)
#plt.plot(df[0][0],df[0][1],'rD',df[1][0],df[1][1],'bD')
plt.show()

'''silhouettescore=[]
for i in range(2,10):
    kmeans=KMeans(n_clusters=i,random_state=123).fit(feature)
    score=silhouette_score(feature,kmeans.labels_)
    silhouettescore.append(score)
#plt.figure(figsize=(10,6))
plt.plot(range(2,10),silhouettescore,linewidth=1.5,linestyle='-')
plt.show()'''

'''for i in range(2,7):
    kmeans=KMeans(n_clusters=i,random_state=123).fit(feature)
    score=calinski_harabasz_score(feature,kmeans.labels_)
    print("聚类%d簇的calinski_harabaz分数为：%f" %(i,score))'''

最后

以上就是诚心香菇为你收集整理的机器学习基础练习题（4）聚类分析作业题目的全部内容，希望文章能够帮你解决机器学习基础练习题（4）聚类分析作业题目所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。