机器学习基石-作业二-第10题分析

题目如上图所示，答案是：；在网上看到的答案中有一个很好的解释就是说在一个n纬的欧几里德空间里，分别按照参数做一个垂直于每个轴的超平面，这些超平面能够打散这么多个点。首先我承认这个事实，具体的证明还没做过。这篇博文的主要作用是把题目转换成前面的描述，也就是说明两个问题是等价的。不想太简单，也不想太复杂，就拿二维平面来举例子了。

一下的讨论都在二维空间中进行：

首先来看S 是一个的向量的集合，在二维空间里就是的集合；更具体的来看：

；S是h的参数

接着是t，这个t向量在二维空间中就是的向量；t是h的参数

接着是输入x，这个x向量在二维空间中也是的向量；x是自变量

最后到了h，这个h首先通过比较x与t的每一个分量（就像decision stump一样），把x转换为一个,然后当时输出1，时输出-1；

到这里可能还是有些抽象，所以下面举一个具体的假设：

 , ; 对应的样本点是{X1=(1,1),X2=(6,6),X3=(3,8),X4=(5,5)}

把样本点带入,可以得到 Y1=-1,Y2=1,Y3=1,Y4=-1;

把t的两个分量作为两个边界，也就是在二维看空间中，把他们看成x=3.6和y=5.2这两条直线；那么平面中的点就会被划分到4个区域中，如下图所示：

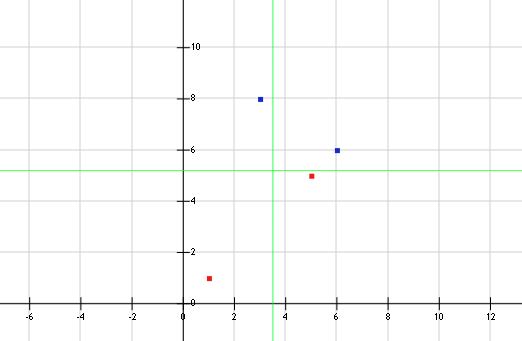
(蓝色为正例，红色为反例），这其实就是在用垂直于轴的线来划分这个平面。

这个过程其实是这样的，

通过把x与t比较把四个区域中的点全部打上了各自的标记，如下图所示：

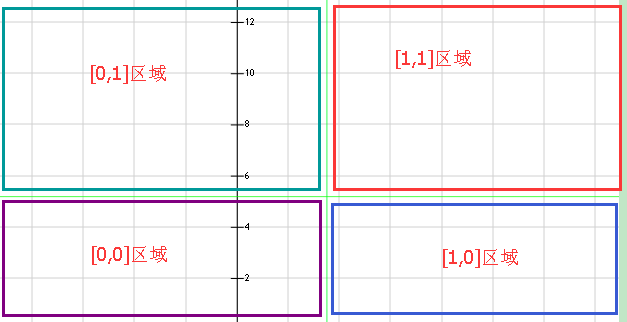
拿[1,1]区域来说，所有在这个区域的点在看来都是向量；也就是说经过了t的处理，在眼中就只有

这四类点。

然后S就上场了，的参数，同时又说，包含在S中的是1，不在S中的是-1；也就是给每个区域赋值了分类标记，如下图：

到这里，可以明确的说，就是用两条垂直于轴的直线在划分平面。

那么假设空间H中，包含着各种的t和S所决定的h；H的能力也就自然是分别按照参数做一个垂直于每个轴的超平面，然后给每一个小区域赋值不同的类别标记了。

最后

以上就是魁梧啤酒为你收集整理的机器学习基石-作业二-第10题分析的全部内容，希望文章能够帮你解决机器学习基石-作业二-第10题分析所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。