'''
两种卷积计算方式对比:
1、调用库函数
2、先计算两者的傅里叶变换,再相乘,再求逆变换
'''
import matplotlib.pyplot as plt
from scipy import signal
import numpy as np
x = [1,2,0,1]
h = [2,2,1,1]
L = len(x) + len(h) - 1
XE = np.fft.fft(x, L)
HE = np.fft.fft(h, L)
tmp = XE*HE
y1 = np.fft.ifft(tmp)
k = []
for i in range(L):
k.append(i)
plt.subplot(2,1,1)
plt.stem(k, y1)
plt.title('Result of Linear Convolution y1')
plt.xlabel('Time index k')
plt.ylabel('Amplitude')
y2 = np.convolve(x,h)
plt.subplot(2,1,2)
plt.stem(k, y2)
plt.title('Result of Linear Convolution y2')
plt.xlabel('Time index k')
plt.ylabel('Amplitude')
plt.show()
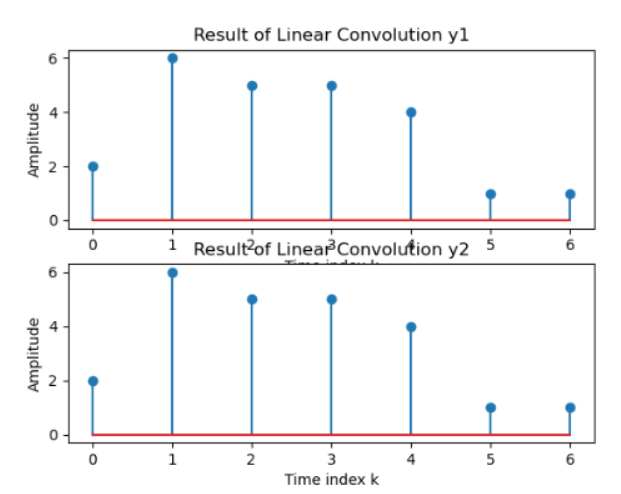
'''
由DFT近似计算 x(t)=e^(-t)*u(t)的幅度频谱并与理论值比较
'''
import numpy as np
import matplotlib.pyplot as plt
#解决汉字显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
fs = 8
N = 32
T = 1/fs
ws = 2 * np.pi * fs
t = np.linspace(0,N-1, N) * T
x = T * np.exp(-t)
Xm = np.fft.fftshift(np.fft.fft(x))
w = -ws/2 + np.linspace(0, N-1, N) * ws / N
wt = np.linspace(-ws/2, ws/2, 1001)
Xw = 1/np.sqrt(1+wt*wt)
plt.plot(wt/np.pi, Xw, 'r')
plt.stem(w/np.pi, np.abs(Xm), 'k')
label = ['理论值','近似值']
plt.legend(label)
plt.show()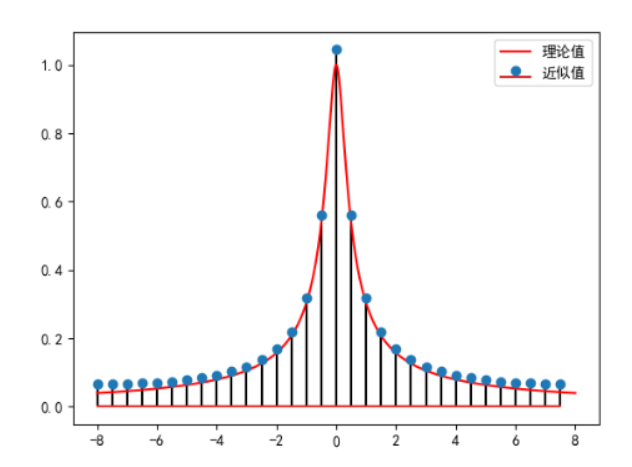
'''
已知连续信号x(t) = cos(2*pi*f1*t)+cos(2*pi*f2*t), f1 = 100Hz, f2=120Hz,
若以抽样频率fsam = 600Hz进行采样,计算由DFT分析其频谱
'''
import numpy as np
import matplotlib.pyplot as plt
#解决汉字显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
N = 50
L = 512
f1 = 100
f2 = 120
fs = 600
T = 1/fs
ws = 2 * np.pi * fs
t = np.linspace(0, N-1,N)*T
x = np.cos(2*np.pi*f1*t) + np.cos(2*np.pi*f2*t)
X = np.fft.fftshift(np.fft.fft(x,L))
w = (-ws/2 + np.linspace(0,L-1,L) * ws / L) / (2*np.pi)
plt.subplot(2,1,1)
plt.plot(w, np.abs(X))
plt.ylabel("幅度谱")
N = 48
L = 512
f1 = 100
f2 = 120
fs = 600
T = 1/fs
ws = 2 * np.pi * fs
t = np.linspace(0, N-1, N)*T
x = np.cos(2*np.pi*f1*t) + np.cos(2*np.pi*f2*t)
wh = np.hamming(N)
x = x*wh
X = np.fft.fftshift(np.fft.fft(x,L))
w = (-ws/2 + np.linspace(0,L-1,L) * ws / L) / (2*np.pi)
plt.subplot(2,1,2)
plt.plot(w, np.abs(X))
plt.ylabel('幅度谱')
plt.show()
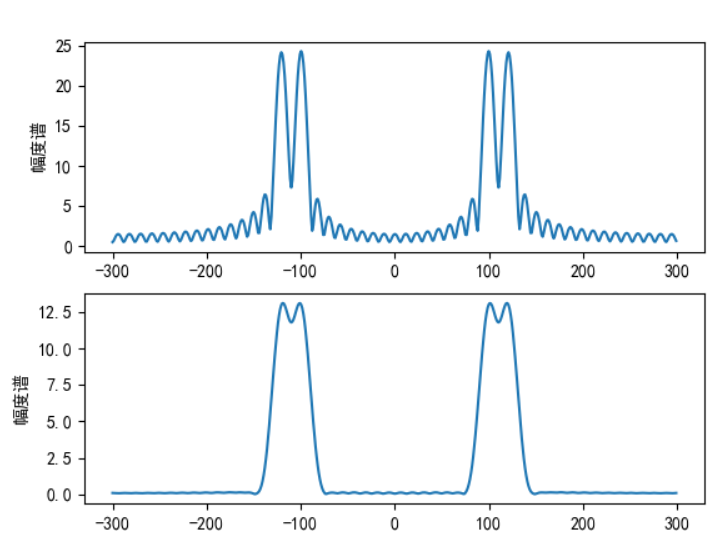
最后
以上就是朴素枕头最近收集整理的关于数字信号处理python代码(陈后金老师书籍第二章)的全部内容,更多相关数字信号处理python代码(陈后金老师书籍第二章)内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复