Pytorch 深度学习实践-02-[Linear Model]

Date: 2021-12-17

Repositity: Gitee

0. 前言

通常深度学习模型的训练流程可以简单分为以下4个部分：

• 准备数据集（包含预处理）
• 选择或设计模型（包含loss和优化器）
• 训练（找到最佳的模型参数）
• 推理（部署）

接下来从基础的线性模型入手展开。

1. 数据集注意事项

这里以学习时间和成绩作为样本，考虑篇幅这里仅用文字描述。

""" Dataset """
# hours
[1, 2, 3, 4]
# points
[2, 4, 6, ?]

如上所示，这里给出数据集，以及问题：当学习时间为4小时时对应的分数应该是多少？这里对数据集进行分割，将其分为训练集和测试集两部分。

""" Train data """
# hours: x
[1, 2, 3]
# points: y
[2, 4, 6]
""" test data """
[4], [?]

这里训练数据中可以看到对应的时间（输入）和分数（输出），相当于提前已知了输入对应的结果，这种带有输出标签的任务即常说的监督学习Supervised Learning。需要注意：

• 测试集我们是不能提供给模型训练的，其用于模型性能的评估；
• 针对上述问题，通常我们的做法是将训练集拆分一小部分出来作为验证集进行训练期间的评估。

2. 模型设计

如何找到适合我们需求的模型呢？通常在机器学习中会先用线性模型查看是否在该数据集上有效。
$$\hat{y}=x\ast \omega +b$$
结合前面的数据可知，这里对该公式简化：$\hat{y}=x\ast \omega$，其中，$\omega =2$ 为其解析解。但是机器是不知道模型对应的参数的值 $\omega$ ，通常其会初始化 $\omega$ 为一个随机值，随着模型不断地迭代使得 $\hat{y}$ 逐渐和真实值 $y$ 接近，进而 $\omega$ 逐渐逼近解析解。那么如何评估其是否接近真实值呢？

答案是损失函数loss function，在线性回归中我们通常使用均方误差MSE对性能进行评估。
$$L(\omega )=\frac{1}{n}\sum _{i=1}^n(\hat{y}-f(x_i){)}^2$$
对应上述数据集，公式2可以变化为：
$$cost=\frac{1}{N}\sum _{i=1}^N(\hat{y}-x\ast \omega {)}^2$$
有了损失函数后，可以不断优化迭代权重参数，直到损失接近0。那么有优化问题：
$$w^{\ast }=\arg \underset{\omega }{\min }cost(\omega )$$
如何优化，答案：梯度下降算法，其核心思路是，按照设定的学习率 $\alpha$，沿着负梯度方向更新函数参数，可以指引损失函数逐渐收敛到局部最小值，即：
$$\omega =\omega -\alpha \frac{\partial L}{\partial \omega }$$
下一节将针对该梯度问题展开。

3. 代码实战

这里用一个循环去查看一下针对前述训练集线性模型的最佳参数。

import numpy as np
import matplotlib.pyplot as plt


x_data = [1., 2., 3.]
y_data = [2., 4., 6.]


def forward(x):
    return x * w


def loss(x, y):
    # cal loss: MSE
    y_pred = forward(x)
    return (y_pred - y) * (y_pred - y)


w_list = []
mse_list = []

for w in np.arange(0., 5., 0.1):
    loss_sum = 0.
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val, y_val)
        loss_sum += loss_val
        print('>>>> y: {}, predict: {}, Loss: {}'.format(y_val, y_pred_val, loss_val))
    print('>>>> MSE={}'.format(loss_sum / len(y_data)))
    w_list.append(w)
    mse_list.append(loss_sum / len(y_data))


plt.plot(w_list, mse_list)
plt.xlabel('w')
plt.ylabel('loss')
plt.show()

4. 使用Axes3D下的plot_surface

import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

""" init 3d surface """
fig = plt.figure()
ax = Axes3D(fig)

# generate meshgrid data
x = np.arange(-5, 10, 0.05)
y = np.arange(-5, 10, 0.05)
w, b = np.meshgrid(x, y)

""" Eq: y = 4x + 6, cal loss """
loss = (w * x + b - x * 4 + 6) ** 2

""" draw loss by plot_surface """
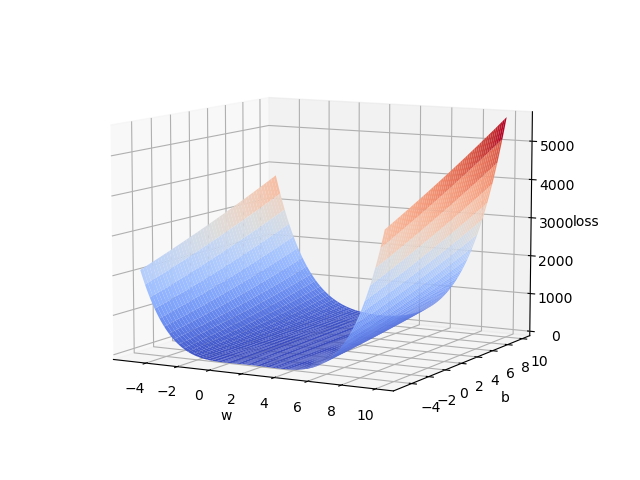
ax.plot_surface(w, b, loss, cmap=matplotlib.cm.coolwarm)
ax.set_xlabel('w')
ax.set_ylabel('b')
ax.set_zlabel('loss')
plt.show()

测试结果如下：

最后

以上就是忧虑朋友为你收集整理的Pytorch 深度学习实践-02-[Linear Model]的全部内容，希望文章能够帮你解决Pytorch 深度学习实践-02-[Linear Model]所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。