Lecture 9:Linear Regression

Linear Regression Problem

例子：机器学习决定发放给用户的信用卡额度，和之前不同的是这个问题输出不是是/否，而是一个实数值。

线性回归的假设：

$x=(x_0,x_1,...,x_d)$代表用户的各项特征（特征向量）

我们希望输出的信用卡额度与特征的加权和非常接近：$y\approx {\sum }_{i=0}^d{w}_i{x}_i$

那么线性回归的假设形式：$h(x)=w^{T}x$

这个假设的形式与perceptron有些类似，但没有sign的过程

以一维特征向量和二维特征向量为例，线性回归的目标是在空间内找到一条直线或者平面，使样本点与之更加接近，或者说使residual最小：

一般线性回归使用squared error来衡量误差：

Linear Regression Algorithm

$E_{in}(w)$是关于权重的函数，我们如何找到合适的$w$使得$E_{in}(w)$最小？

把$E_{in}(w)$的公式转化为矩阵运算的形式（把多个向量的平方和转化为一个大向量长度的平方）：

现在，我们的目标转化为：
$$mi{n}_w{E}_{in}(w)=\frac{1}{N}||Xw-y|{|}^2$$
$E_{in}（w）$一般有可微分、连续、凸函数的性质，所以只要找到梯度为0的位置，就是在函数图像上的最低点，也就是$E_{in}(w)$的最小值

求梯度：

梯度为0时，求出权重：

$X^{T}X$如果是可逆的，则$w=(X^{T}X{)}^{-1}{X}^{T}y$,只要样本数量$N$远大于$d+1$就能保证矩阵的逆是存在的，称之为非奇异矩阵。

但是如果是奇异矩阵，不可逆怎么办呢？其实，大部分的计算逆矩阵的软件程序，都可以处理这个问题，也会计算出一个逆矩阵。所以，一般伪逆矩阵是可解的。

对比梯度下降法和正规方程法：

梯度下降法：

• 需要人为选择学习率
• 需要进行多次迭代
• 样本特征向量的维度很大时效果也很好

正规方程法：

• 不用确定学习率
• 不需要迭代
• 计算矩阵的逆运算时需要的时间复杂度是矩阵维度的三次方，因此当n过大时，使用正规方程组的时间会很长

Generalization Issue

下面说明线性回归可以通过最小二乘方法计算得到好的$E_{in}$和$E_{out}$

hat matrix的物理意义：$\hat{y}$

如图，$y$是$N$维空间中的向量（这里的$N$指的是样本数据个数），代表样本数据实际输出值，粉色区域代表的是输入矩阵$X$与不同的权重$w$相乘构成的空间，所以预测的输出向量$\hat{y}$是在粉色空间中的一个向量。

机器学习的目标就是使$\hat{y}$尽可能接近$y$，那么显然最好的是$y$直接在粉色空间上垂直投影，hat matrix就表示将$y$投影到$\hat{y}$这一操作：$\hat{y}=Hy$

那么从这个角度讲，$y-\hat{y}=y-Hy=(I-H)y$,所以$I-H$表示的是将$y$投影到$y-\hat{y}$的操作。

通过推导可以得到$trace(I-H)=N-(d+1)$,物理意义是将$N$维向量向$d+1$维空间投影时，余数剩余的自由度最大只有$N-(d+1)$

如果存在噪声，如下图：

我们可以把$y$看作是理想输出$f(x)$加上noise的结果

上面的推导中$y$通过$I-H$转化为$y-\hat{y}$,而noise与y是线性变换关系，那么根据线性函数知识，我们推导出noise经过$I-H$也能转换为$y-\hat{y}$

所以：
$$E_{in}(w_{LIN})=\frac{1}{N}||y-\hat{y}|{|}^2=\frac{1}{N}||(I-H)noise|{|}^2=\frac{1}{N}(N-(d+1))|noise|{|}^2$$
(图中${\sigma }^2$是描述噪声的一个量)

最终得到：

把这两个变量画出来：

当N足够大时，二者逐渐接近，且收敛于${\sigma }^2$,二者之差为$2(d+1)/N$，(泛化误差)。这就类似VC理论，证明了当N足够大的时候，这种线性最小二乘法是可以进行机器学习的，算法有效！

Linear Regression for Binary Classification

能否将线性回归的方法应用于线性分类问题？

先对比一下两种方法：

下图展示了两种错误衡量方式的关系：$er{r}_{0/1}\le er{r}_{sqr}$

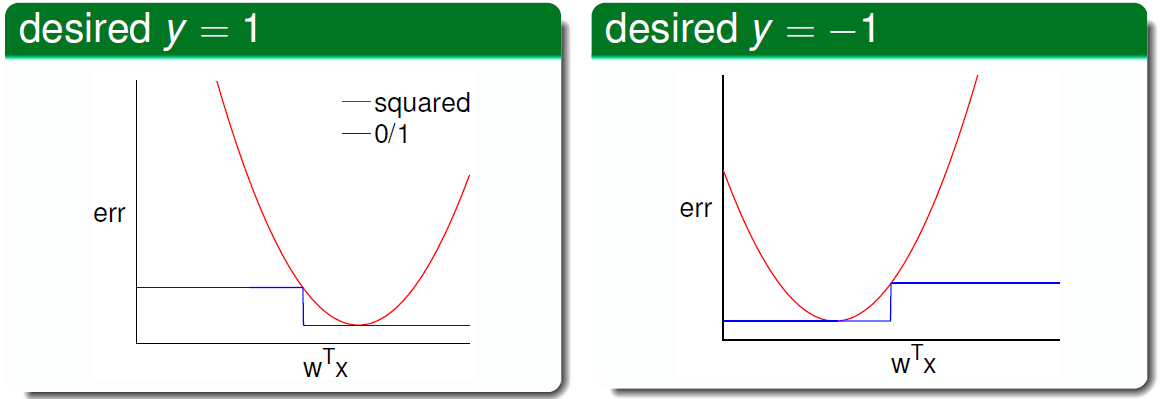
根据之前的VC理论，$E_{out}$的上界满足：

所以$E_{out}$的上界只是变得更加宽松了，而不是没有上界，所以如果回归误差作为上限很小，那么分类误差也会很小，用线性回归方法仍然可以解决线性分类问题，效果不会太差。

最后

以上就是狂野香氛为你收集整理的【台大林轩田《机器学习基石》笔记】Lecture 9——Linear RegressionLecture 9:Linear Regression的全部内容，希望文章能够帮你解决【台大林轩田《机器学习基石》笔记】Lecture 9——Linear RegressionLecture 9:Linear Regression所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。