变限积分函数

1，定义

如果f(x)在区间[a, b]上连续，设x为[a,b]上的一点，考察下面的函数：

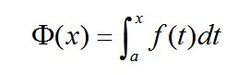
1.1 这个函数的变量只出现在积分上限，所以叫变上限函数；同理，如果在下面，则叫变下限函数；
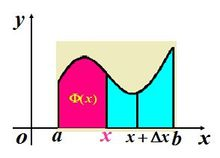
1.2 从几何上来看，该函数表示区间[a,x]上曲边梯形的面积（如下图）。

1.3 积分变限函数是一类重要的函数，它最著名的应用是在牛顿一莱布尼兹公式的证明中．事实上，积分变限函数是产生新函数的重要工具，尤其是它能表示非初等函数，同时能将积分学问题转化为微分学问题。积分变限函数除了能拓展我们对函数概念的理解外，在许多场合都有重要的应用。

2，函数性质

2.1 连续性
【定理一】若函数f(x)在区间[a,b]上可积，则积分变上限函数在[a,b]上连续。
2.2 导数定理
【定理二】如果函数f(x)在区间[a，b]上连续，则积分变上限函数在[a,b]上具有导数，并且导数为：

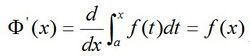
证明过程：

2.3 导数推广

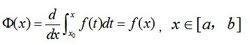
注：（1），$x_0为[a,b]上的任意一点；$
（2），a可以为负无穷，b可以为正无穷；
（3），此定理是变限积分的最重要的性质，掌握此定理需要注意两点：第一，下限为常数，上限为参变量x（不是含x的其他表达式）；第二，被积函数f(x)中只含积分变量t，不含参变量x。

2.4 导数进一步推广

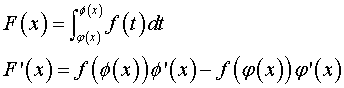
注：被积函数f(x)中只含积分变量t，不含参变量x。

2.5 原函数存在定理
若函数f(x)在区间[a,b]上连续，则积分变上限函数就是f(x)在[a,b]上的一个原函数。

3，函数应用

3.1 利用变限积分求原函数
3.2 化积分问题为微分问题
3.3 用变限函数求定积分
3.4 变量替换是重要方法

Reference

https://baike.baidu.com/item/积分变限函数/339961

最后

以上就是忧虑大叔为你收集整理的变限积分函数的全部内容，希望文章能够帮你解决变限积分函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。