解释一下积分变上限函数

本文从以下几个方面讨论这个问题

1. 什么是变上限函数？
2. 它如何求导？
3. 广义的变上限函数求导方法–用牛莱公式一步到位！

1、积分上限函数的通俗理解

先看个例子：

考虑一个定积分：
$$A(b)={\int }_a^{b}f(t)dt\text{\hspace{1em}(1)}$$
如果把的上限在变化的话，那么这个过程就应该是这样的：

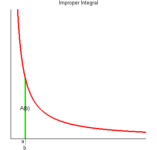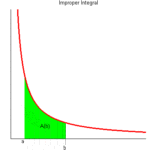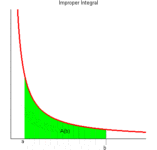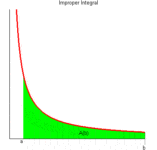
图片来自网络侵删。

上图其实是变上限函数 $A(b)={\int }_a^{b}f(t)dt$ 的几何变化情况, 当 $b$ 为变量时这个綠色部分的 面积就是关于 $b$ 的函数。这时我们把 $b$ 换成 $x,A(b)$ 记成 $F(x),$ 它就交成了这个函数：
$$F(x)={\int }_a^{x}f(t)dt\text{\hspace{1em}(2)}$$
称为积分变上限函数，有的地方又叫变上限函数，变上限积分。通俗地讲：就是定积分的上限是一个变量，而不是常量。

2、积分变上限函数的性质和导数

这个函数有很多良好的性质，其中一个最爽的性质就是：

• 如果 $f(t)$ 连续，那么 $F(x)$ 连续且可导。

考虑它的导数定义式:
$$\begin{array}{rl}\underset{\Delta x\to 0}{\lim }\frac{F(x+\Delta x)-F(x)}{\Delta x}=& \underset{\Delta x\to 0}{\lim }\frac{{\int }_a^{x+\Delta x}f(t)dt-{\int }_a^{x}f(t)dt}{\Delta x}\\ & =\underset{\Delta x\to 0}{\lim }\frac{{\int }_x^{x+\Delta x}f(t)dt}{\Delta x}\end{array}\text{\hspace{1em}(3)}$$

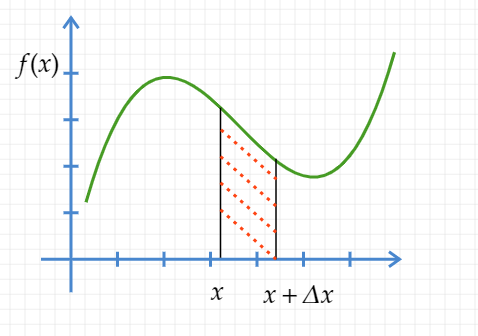
注意（3）式就很有意思了，它表示下图所示的红斜杠阴影部分的面积：

这里要用到积分中值定理：
$${\int }_x^{x+\Delta x}f(t)dt=\Delta x\cdot f(\xi )\text{\hspace{1em}(4)}$$
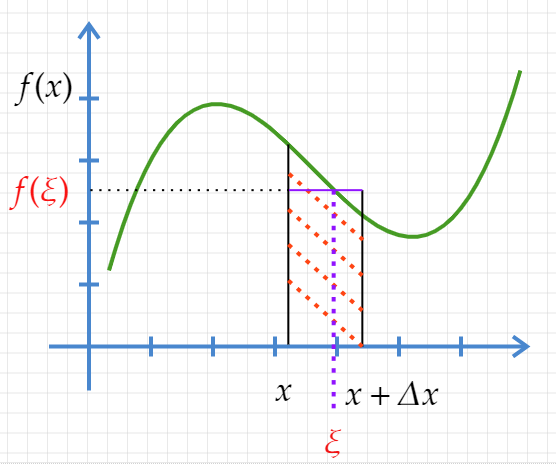
简单地说就是有个点 $\xi$, 使得在这一点对应的 $f(\xi )$ 作为高, $\Delta x$ 作为密的拒形面积, 等于红 綫阴影部分的曲边梯形的面积。注意这个 $\xi$ 是在 $[x,x+\Delta x]$ 之间的，那么如果 $\Delta x\to 0$ 这个 $\xi$ 就会无限趋于 $x$ 。此时上述矩形的面积也就无限趋近于曲边梯形的面积。

于是把（４）代入（３）就得到：

$$\underset{\Delta x\to 0}{\lim }\frac{{\int }_x^{x+\Delta x}f(t)dt}{\Delta x}＝\underset{\Delta x\to 0}{\lim }\frac{\Delta x\cdot f(\xi )}{\Delta x}=\underset{\Delta x\to 0}{\lim }f(\xi )=f(x)\text{\hspace{1em}(5)}$$

注意：这步推导成立的前提是 $f(x)$ 连续。

再把（5）代回（3），再注意到（3)其实就是 $F(x)$ 的导数，于是：

$$F^{\prime }(x)=\frac{d\left[{\int }_a^{x}f(t)dt\right]}{dx}=\underset{\Delta x\to 0}{\lim }\frac{F(x+\Delta x)-F(x)}{\Delta x}=f(x)\text{\hspace{1em}(6)}$$
一元函数连续一定可导，所以证明完成。

3、进入正题：用牛莱公式重新认识积分变上限函数

牛莱公式的定义是：

$${\int }_a^{b}f(t)dt=F(b)-F(a)\text{\hspace{1em}(7)}$$
如果我直接用它来研究变上限函数会是怎样：

$${\int }_a^{x}f(t)dt=F(x)-F(a)\text{\hspace{1em}(8)}$$
左右相等对不对？所以我左边要求导是不是右边也对应求导？

现在正题来了，直接考虑右端求导：

由于左右边求导等于右边求导，那么也就能得到（6）式。

接下来才是最正的题：

考虑（2）式最一般的情形：

$$\Phi (x)={\int }_{a(x)}^{b(x)}f(t)dt\text{\hspace{1em}(9)}$$
许多人第一次见到这个东西就吓到了，书上动不动就给你拆开分成两个。完全用不着！

这里仍然设 $F(x)$ 是 $f(x)$ 的原函数，那么根据牛莱公式就有：

$$\Phi (x)={\int }_{a(x)}^{b(x)}f(t)dt=F[b(x)]-F[a(x)]\text{\hspace{1em}(10)}$$
那么此时再对 $\Phi (x)$ 求导是不是就感觉容易多了，没错，就是复合函数求导：

$${\Phi }^{\prime }(x)={\left(F[b(x)]-F[a(x)]\right)}^{\prime }=F^{\prime }[b(x)]\cdot b^{\prime }(x)-F^{\prime }[a(x)]\cdot a^{\prime }(x)\text{\hspace{1em}(11)}$$
搞定！

最后

以上就是苗条花生为你收集整理的解释一下积分变上限函数的全部内容，希望文章能够帮你解决解释一下积分变上限函数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。