有向图的环和有向无环图

46 阅读 0 评论 31 点赞

我是靠谱客的博主清爽山水，最近开发中收集的这篇文章主要介绍有向图的环和有向无环图，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

本篇主要分享关于有向图的环和有向无环图（DAG，估计做大数据的同学到处都可以看到），所以相关概念我就不做详细介绍了。

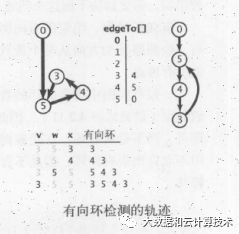
640?wx_fmt=png

用有向图中各个节点代表着一个又一个的任务，而其中的方向代表的任务的执行顺序。而方向代表着这个在执行这个任务之前必须完成其他节点，例如上图中在5执行必须执行3和0 节点。

所以可以想到有向图中有向环的检测非常重要，例如上面要是5之前 3要执行，3之前4要执行，4之前5要执行，那么着三个限制条件永远事不可能被执行的，要是一个优先级限制的问题中存在有向环，那么这个问题肯定是无解的。

有向环的检测的理念是我们找到了一条边v-》w 要是w已经存在在栈中，就找到了一个环，因为栈中表示的是一条有w-》v的路径，而v-》w正好补全了这个环。也就是存在有向环。所以这个优先任务是有问题的。

public class DirectedCycle {
private boolean[] marked;
   private int[] edgeTo;
   private Stack<Integer> cycle;
   private boolean[] onStack;

   public DirectedCycle(Digraph G) {

onStack = new boolean[G.V()];
      edgeTo = new int[G.V()];
      marked = new boolean[G.V()];
      for (int v = 0; v < G.V(); v++) {
if (!marked[v]) {

dfs(G, v);
         }

}

}

private void dfs(Digraph G, int v) {

onStack[v] = true;
      marked[v] = true;
      for (int w : G.adj(v)) {
if (this.hasCycle()) {
return;
         } else if (!marked[w]) {

edgeTo[w] = v;
            dfs(G, w);
         } else if (onStack[w]) {

cycle = new Stack<Integer>();
            for (int x = v; x != w; x = edgeTo[x]) {

cycle.push(x);
            }


cycle.push(w);
            cycle.push(v);
         }

}

onStack[v] = false;
   }

public boolean hasCycle() {
return cycle != null;
   }

public Iterable<Integer> cycle() {
return cycle;
   }
}