21、数据结构与算法 - 图最短路径（一）Dijkstra算法图最短路径

53 阅读 0 评论 35 点赞

我是靠谱客的博主冷静冥王星，最近开发中收集的这篇文章主要介绍21、数据结构与算法 - 图最短路径（一）Dijkstra算法图最短路径，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

图最短路径

图的最短路径是求图上两个点相连的话最短的路径不需要连接所有点

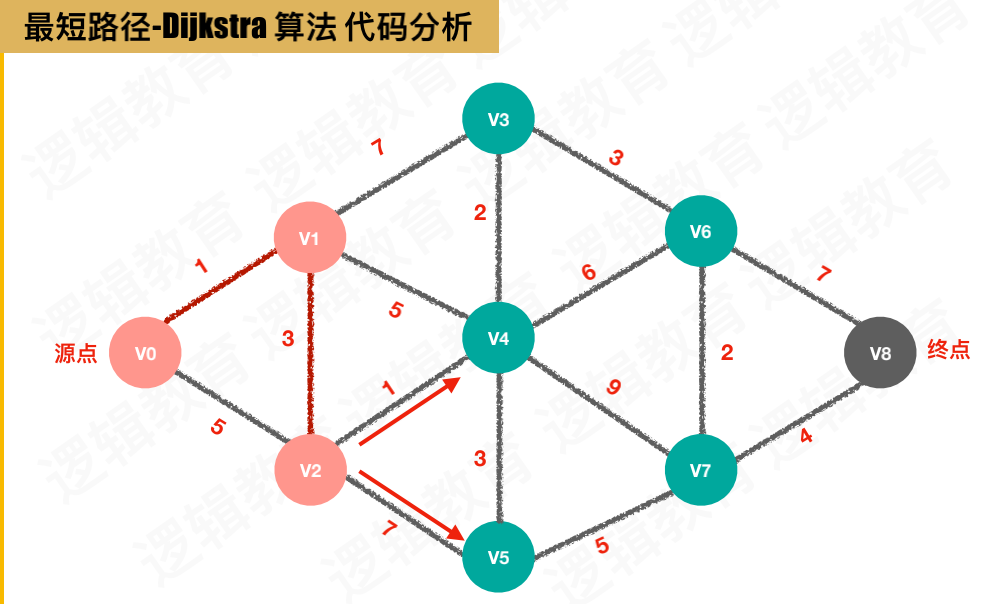
如下图，要从源点 v0 到终点 v8

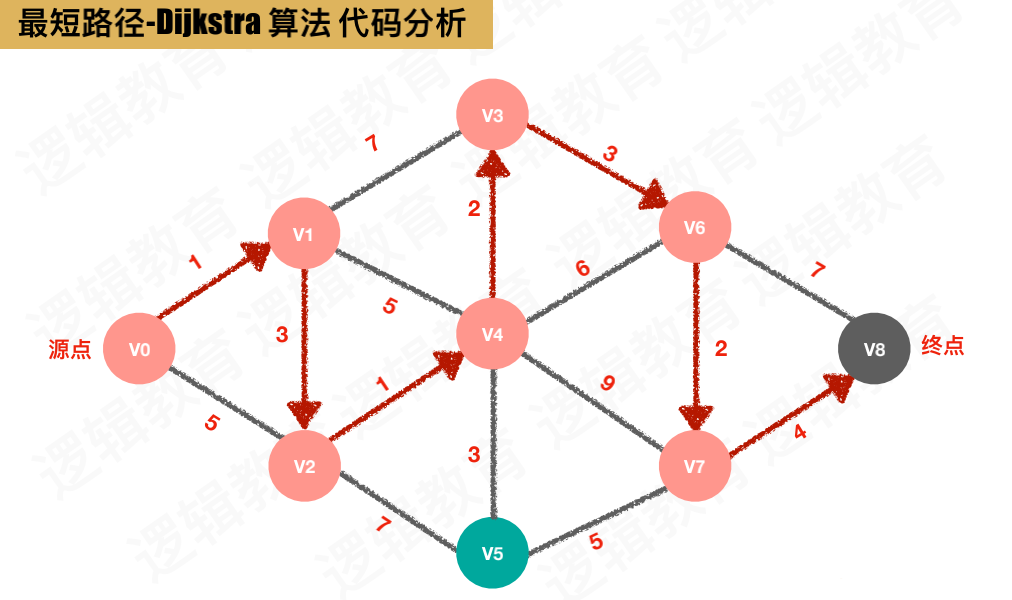
图的邻接矩阵存储

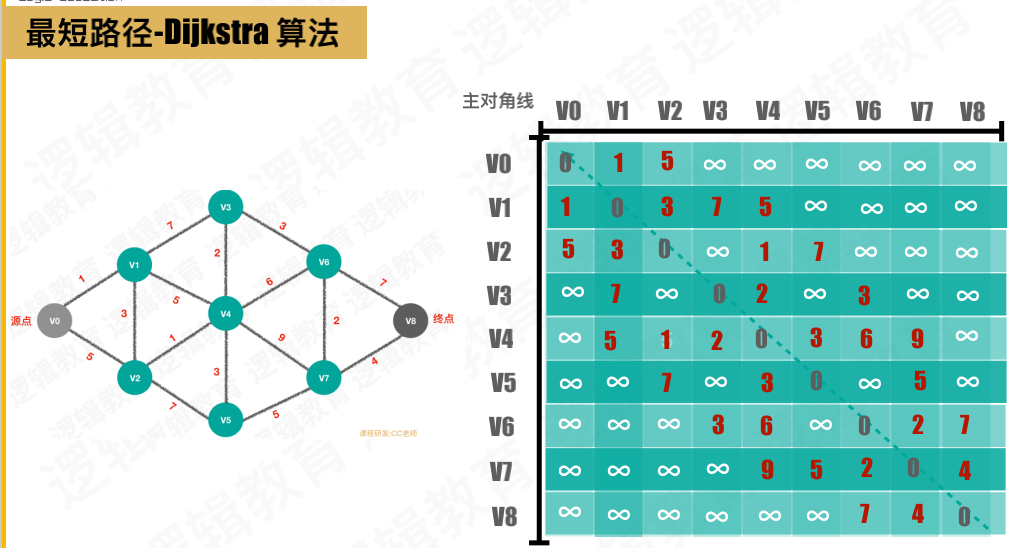
最终应求得的结果

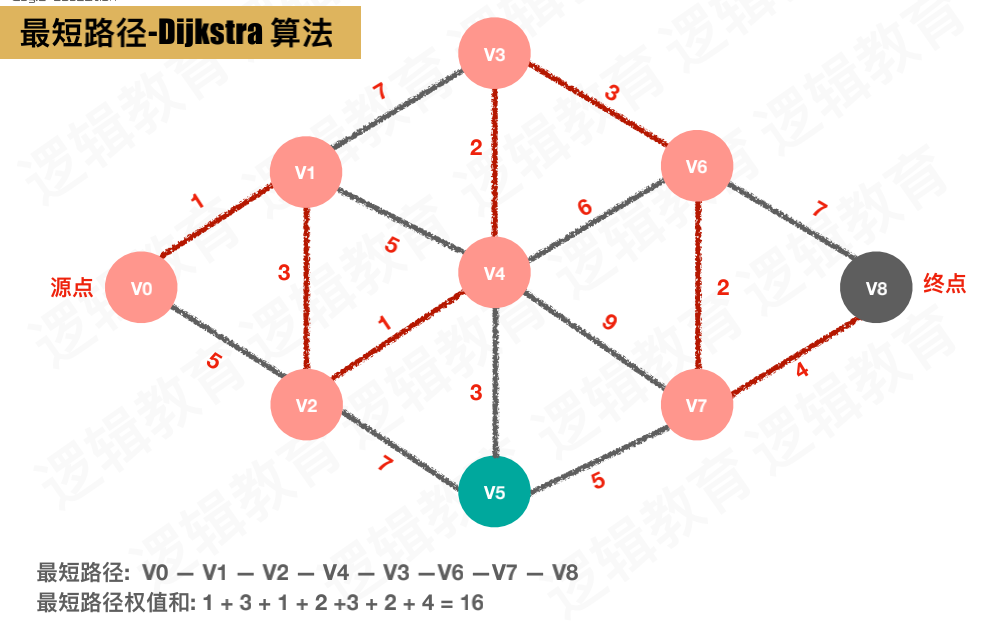
Dijkstra算法

思路分析：

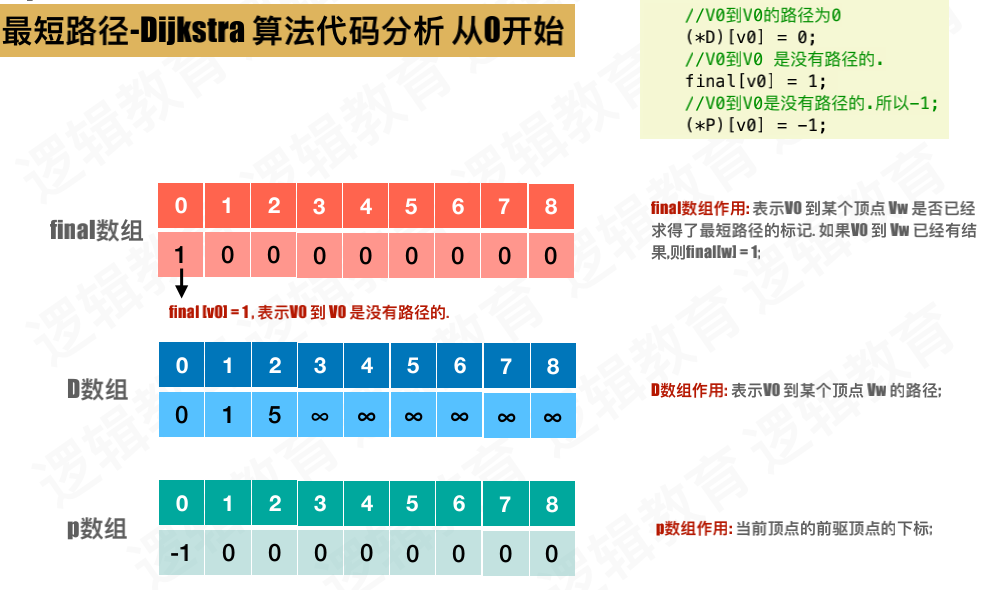
初始化3个数组，

final数组：用来标记顶点是否已经求得最短路径，求得标记为1，没有标记为0.求得过的，不再重复计算
D数组：用来比较V0 到某个顶点的路径（例如V0->V3 = V0->V1+V1->V3,当然也会有多条路径的情况，进行比较如果比当前数组中存的小就更新）
p数组：用来存当前定点的前驱定点的下标，也就是说标记最短路径的途径

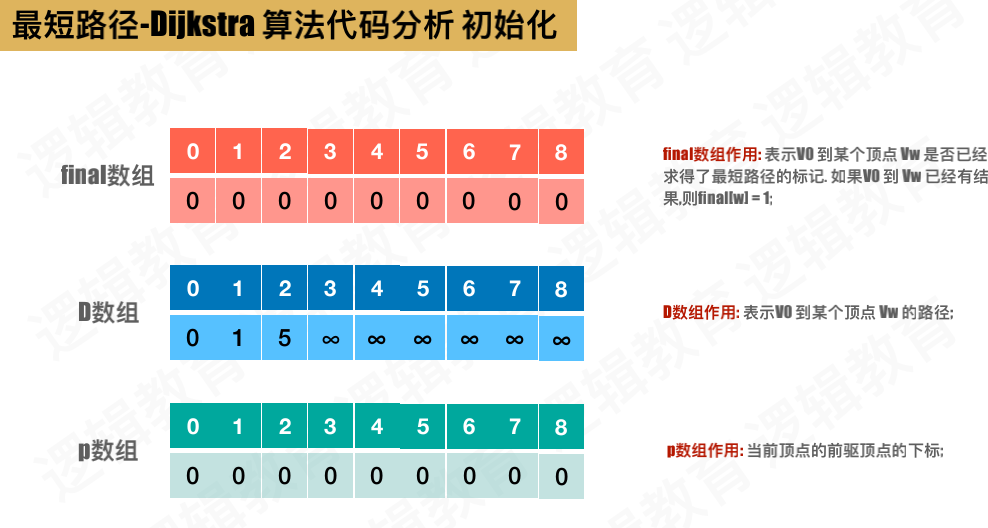
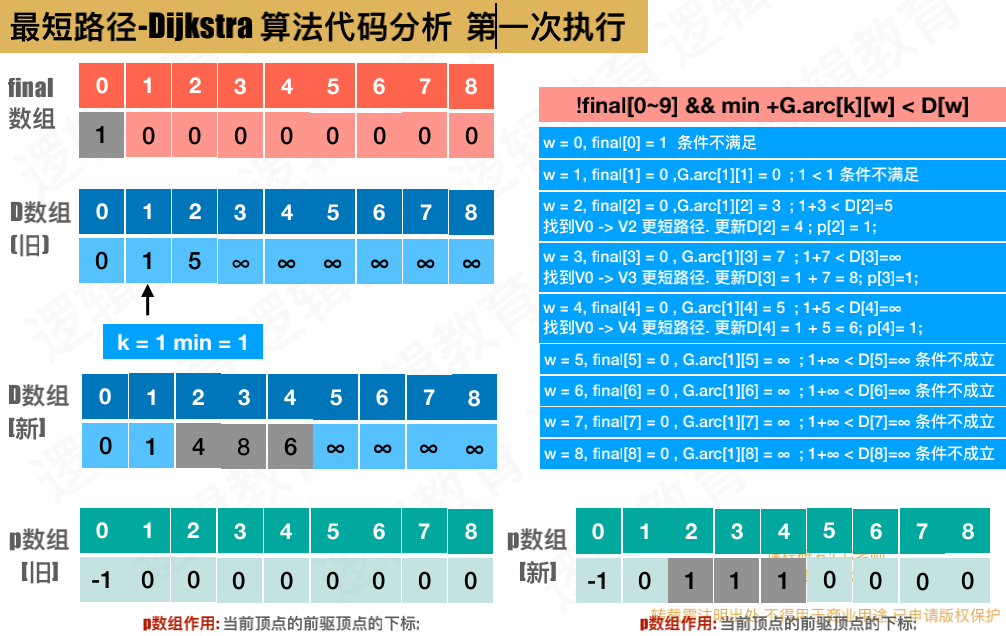
第一次执行

V0->V1

V0 目前能到的顶点及距离标记到D数组中

p数组存一下顶点对应前驱

画图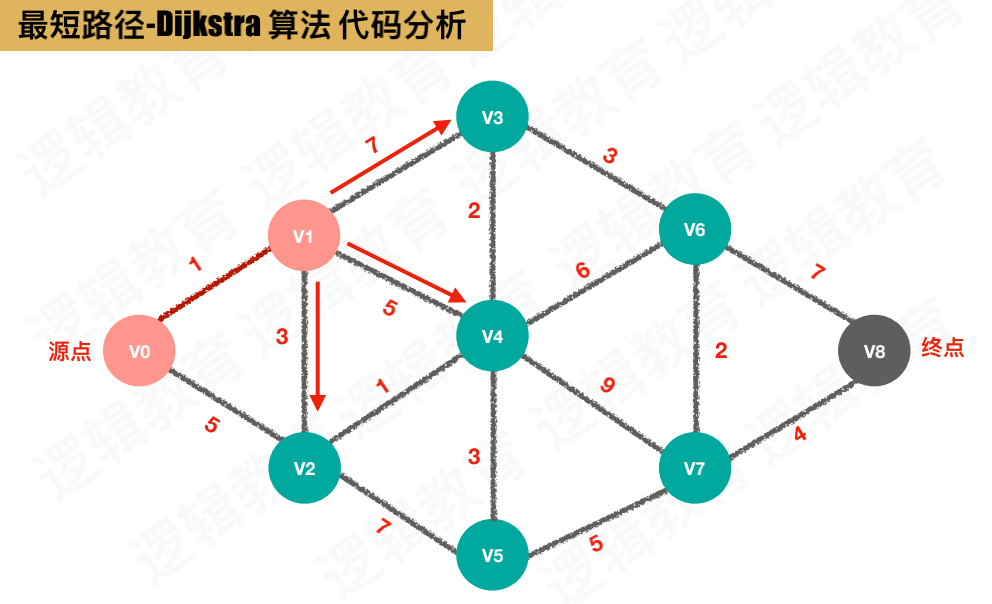

第二次执行，

V0->V4,刚开始是 V0->V1->V4 距离是6

现在，V0->V1->V2->V4 距离是5，

4+1< D[4],所以更新D数组

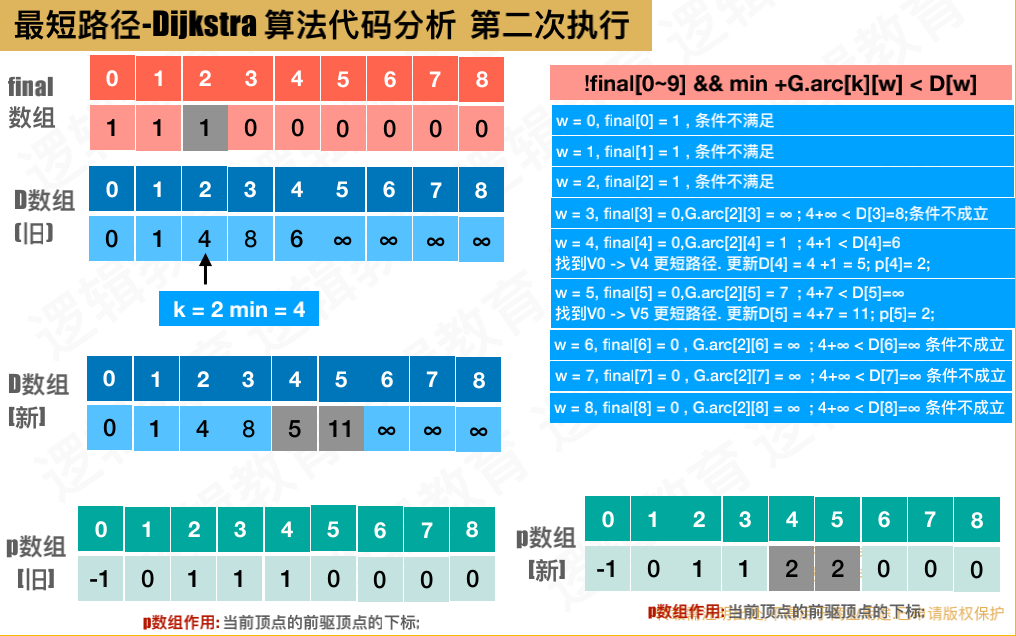
后面是一样的

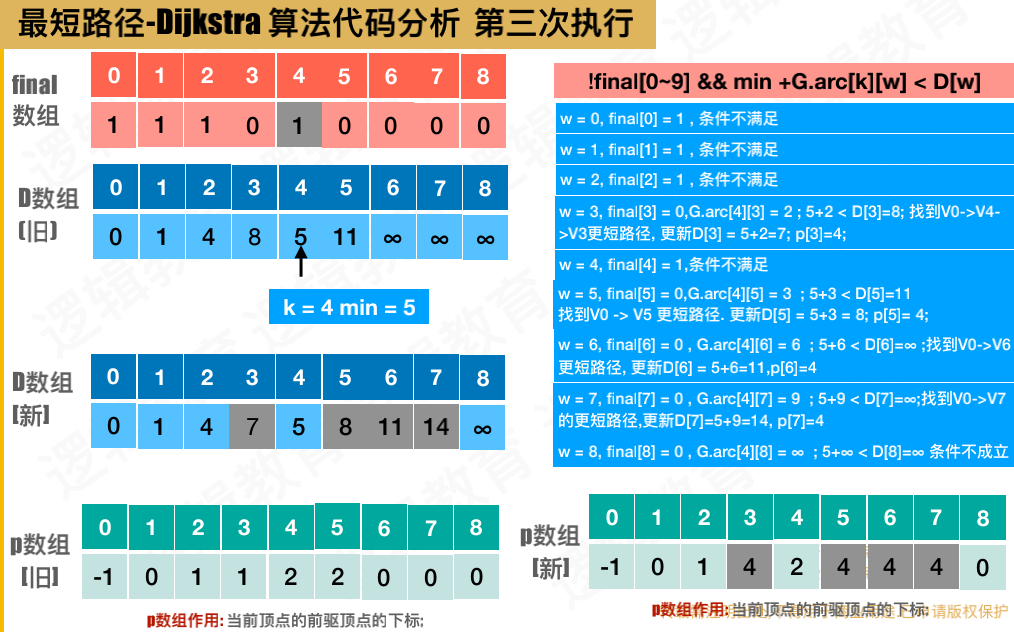
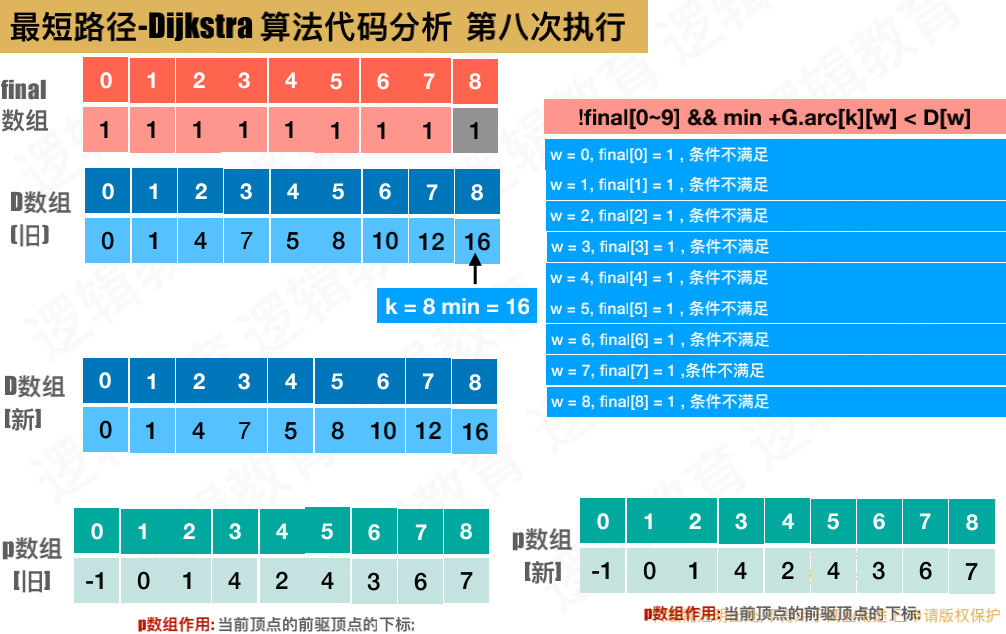
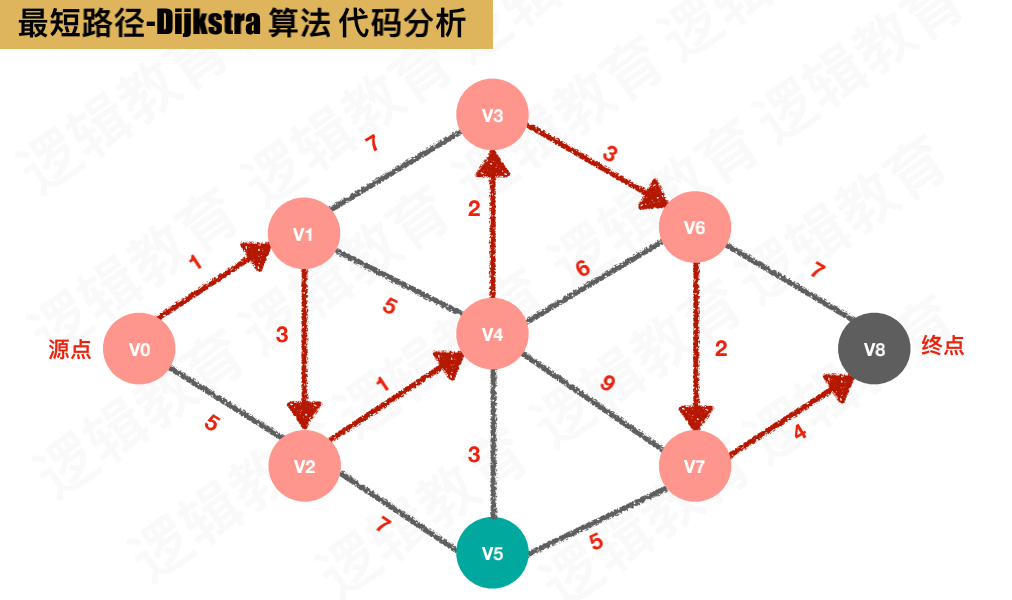
代码实现

#include "stdio.h"
#include "stdlib.h"

#include "math.h"
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXEDGE 20
#define MAXVEX 20
#define INFINITYC 65535

typedef int Status;
typedef struct
{
    int vexs[MAXVEX];
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;
}MGraph;

/*用于存储最短路径下标的数组*/
typedef int Patharc[MAXVEX];
/*用于存储到各点最短路径权值的和*/
typedef int ShortPathTable[MAXVEX];

/*10.1 创建邻近矩阵*/
void CreateMGraph(MGraph *G)
{
    int i, j;
    
    G->numEdges=16;
    G->numVertexes=9;
    
    for (i = 0; i < G->numVertexes; i++)
    {
        G->vexs[i]=i;
    }
    
    for (i = 0; i < G->numVertexes; i++)
    {
        for ( j = 0; j < G->numVertexes; j++)
        {
            if (i==j)
                G->arc[i][j]=0;
            else
                G->arc[i][j] = G->arc[j][i] = INFINITYC;
        }
    }
    
    G->arc[0][1]=1;
    G->arc[0][2]=5;
    G->arc[1][2]=3;
    G->arc[1][3]=7;
    G->arc[1][4]=5;
    
    G->arc[2][4]=1;
    G->arc[2][5]=7;
    G->arc[3][4]=2;
    G->arc[3][6]=3;
    G->arc[4][5]=3;
    
    G->arc[4][6]=6;
    G->arc[4][7]=9;
    G->arc[5][7]=5;
    G->arc[6][7]=2;
    G->arc[6][8]=7;
    
    G->arc[7][8]=4;
    
    
    for(i = 0; i < G->numVertexes; i++)
    {
        for(j = i; j < G->numVertexes; j++)
        {
            G->arc[j][i] =G->arc[i][j];
        }
    }
    
}

/*10.2 求得网图中2点间最短路径
 Dijkstra 算法
 G: 网图;
 v0: V0开始的顶点;
 p[v]: 前驱顶点下标;
 D[v]: 表示从V0到V的最短路径长度和;
 */
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{
    int v,w,k,min;
    k = 0;
    /*final[w] = 1 表示求得顶点V0~Vw的最短路径*/
    int final[MAXVEX];
    
    /*1.初始化数据*/
    for(v=0; v<G.numVertexes; v++)
    {
        //全部顶点初始化为未知最短路径状态0
        final[v] = 0;
        //将与V0 点有连线的顶点最短路径值;
        (*D)[v] = G.arc[v0][v];
        //初始化路径数组p = 0;
        (*P)[v] = 0;
    }
    
    //V0到V0的路径为0
    (*D)[v0] = 0;
    //V0到V0 是没有路径的.
    final[v0] = 1;
    //v0到V0是没有路径的
    (*P)[v0] = -1;
    
  
    
    //2. 开始主循环,每次求得V0到某个顶点的最短路径
    for(v=1; v<G.numVertexes; v++)
    {
        
        //当前所知距离V0顶点最近的距离
        min=INFINITYC;
        /*3.寻找离V0最近的顶点*/
        for(w=0; w<G.numVertexes; w++)
        {
            if(!final[w] && (*D)[w]<min)
            {
                k=w;
                //w顶点距离V0顶点更近
                min = (*D)[w];
            }
        }
        
        //将目前找到最近的顶点置为1;
        final[k] = 1;
        
        /*4.把刚刚找到v0到v1最短路径的基础上,对于v1 与 其他顶点的边进行计算,得到v0与它们的当前最短距离;*/
        for(w=0; w<G.numVertexes; w++)
        {
            //如果经过v顶点的路径比现在这条路径长度短,则更新
            if(!final[w] && (min + G.arc[k][w]<(*D)[w]))
            {
                //找到更短路径, 则修改D[W],P[W]
                //修改当前路径的长度
                (*D)[w] = min + G.arc[k][w];
                (*P)[w]=k;
            }
        }
    }
}

验证

int main(void)
{
    printf("最短路径-Dijkstra算法n");
    int i,j,v0;
    MGraph G;
    Patharc P;
    ShortPathTable D;
    v0=0;
    
    CreateMGraph(&G);
    
    ShortestPath_Dijkstra(G, v0, &P, &D);
    
    printf("最短路径路线:n");
    for(i=1;i<G.numVertexes;++i)
    {
        printf("v%d -> v%d : ",v0,i);
        j=i;
        while(P[j]!=-1)
        {
            printf("%d ",P[j]);
            j=P[j];
        }
        printf("n");
    }
    
    printf("n最短路径权值和n");
    for(i=1;i<G.numVertexes;++i)
        printf("v%d -> v%d : %d n",G.vexs[0],G.vexs[i],D[i]);
    
    printf("n");
    return 0;
}

结果

最短路径-Dijkstra算法
最短路径路线:
v0 -> v1 : 0 
v0 -> v2 : 1 0 
v0 -> v3 : 4 2 1 0 
v0 -> v4 : 2 1 0 
v0 -> v5 : 4 2 1 0 
v0 -> v6 : 3 4 2 1 0 
v0 -> v7 : 6 3 4 2 1 0 
v0 -> v8 : 7 6 3 4 2 1 0 

最短路径权值和
v0 -> v1 : 1 
v0 -> v2 : 4 
v0 -> v3 : 7 
v0 -> v4 : 5 
v0 -> v5 : 8 
v0 -> v6 : 10 
v0 -> v7 : 12 
v0 -> v8 : 16